m0936

1

Пример 1. Функция y e x2 имеет в точке x 0 устрани-

мый разрыв (см. задачу 7.2.3, г). Если доопределить эту функцию в точке x 0 значением ее предела, то получим неэлементарную непрерывную во всей области существования функцию

Пример 2. Функция у = arctg1 имеет в точке x 0 раз- x

рыв первого рода (см. задачу 7.2.3, в).

Пример 3. При исследовании динамики механических систем с учетом сухого (кулоновского) трения используют функции с разрывами первого рода. Пусть v – относительная скорость перемещения трущихся поверхностей. Сила трения Fтр равна:

зических соображений значением

Fтр 0 0.

Пример 4. Функция у = tg x

(рис. 7.2) имеет в точке x разрыв

Пример 5. Функция у = sin 1 x

имеет в точке x 0 разрыв второго рода, так как можно доказать, что ни

один из односторонних пределов не Рис. 7.2. Функция y = tg x существует.

61

Используя понятие односторонних пределов, можно ввести третье определение непрерывности функции.

Если левый и правый пределы функции y f x в точке x a равны между собой и равны значению функции в этой точ-

ке: lim f x lim f x f a , то функция непрерывна в этой

x a 0 x a 0

точке.

Задачи к разделу 7.3

7.3.1. Найти точки разрыва функций и установить их вид:

7.3.2. Найти точки разрыва функций и установить их вид:

2

7.3.3.Доказать, что ни один из односторонних пределов

функции y sin 1 не существует. x

7.4. Способы вычисления односторонних пределов

Односторонние пределы можно вычислять с помощью правил, рассмотренных в теме 6.

При исследовании поведения функции в окрестности точек разрыва более удобным представляется способ вычисления пределов, основанный на представлении аргумента функции под знаком предела в виде x a в окрестности предельной точки x a ( x – бесконечно малая величина). Например, левый предел f a 0 определяют при значениях аргумента x a в ле-

вом полуинтервале проколотой -окрестности предельной точки x a при x a . Бесконечно малая величина x с гео-

62

метрической точки зрения представляет собой расстояние между текущей точкой x и предельной точкой a. Поэтому всегда x a ( 0 0) при левом и при правом пределах.

При вычислении одностороннего предела в функцию подставляют x a при левом пределе и x a при правом пределе и проводят алгебраические операции. При этом беско-

x 3

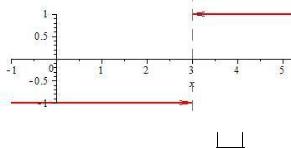
Решение. При x 3 0 x 3 функция имеет точку разрыва

(рис. 7.3).

Рис. 7.3. График функции y x 3 x 3

Замечание. При х = 3 функция не определена, поэтому ветви графика функции в окрестности предельной точки оканчиваются стрелками.

рывность. Найти точки разрыва, определить поведение функции в окрестности точки разрыва.

63

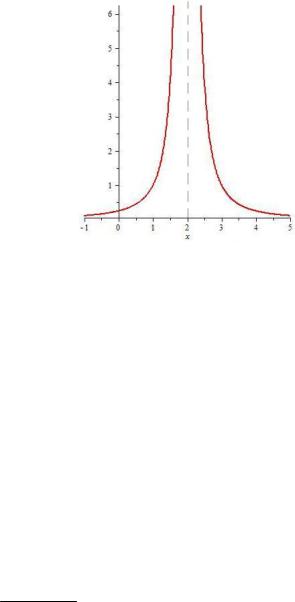
Решение. При всех x 2 функция имеет конечные значения, т.е. непрерывна. В точке x 2 функция имеет разрыв (рис. 7.4).

Определим тип точки разрыва и поведение функции в окрестности этой точки с помощью односторонних пределов.

В точке x 2 функция имеет разрыв второго рода. В окрестности этой точки функция стремится к слева и справа. Прямая x 2, параллельная оси Oy, к которой неограниченно приближаются ветви графика функции, называется вертикальной асимптотой. Интервалы непрерывности: , 2 и 2, . Область существования функции D x x| x , 2 2, .

Пример 3. Определить промежуток, в котором функция

arcsin x 3

y непрерывна. x2 ex

64

Решение. Знаменатель функции не обращается в ноль ни при каких значениях переменной x R. Числитель функции имеет смысл при 1 x 3 1 2 x 4. Таким образом, функция непрерывна на промежутке 2, 4 .

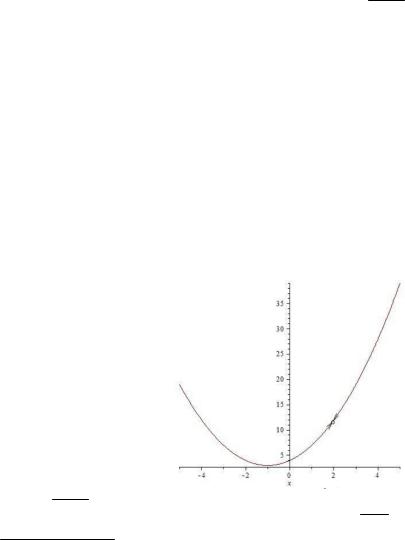
Пример 4. Исследовать непрерывность функции y x3 8. x 2

Решение. Из уравнения x 2 0 следует, что точка x 2 является точкой разрыва функции (рис. 7.5).

Левый предел:

2

12 6 12.

65

Получено почти каноническое уравнение параболы с вершиной в точке O 1, 3 с точкой устранимого разрыва x 2. При x 2 из уравнения параболы следует: y 22 2 2 4 12. Таким

0

образом, раскрытие неопределенностей вида – это, по суще-

0

ству, исключение (устранение) точек устранимого разрыва из области существования функции.

построить ее график.

7.4.2. Найти точки разрыва и односторонние пределы функ-

xx

7.4.5.Исследовать непрерывность функций: а) y x – целая

66

7.4.6. Исследовать непрерывность функций:

7.5. Исследование непрерывности сложной функции

Сложную функцию (композицию функций) вида y f x

можно разложить на две более простые функции за счет введения промежуточного аргумента y f u , u x . При этом функцию y f u называют «внешней» функцией, а u x – «внутрен-

ней» функцией.

При исследовании непрерывности сложной функции ее разрывы имеют место в окрестности тех значений основного аргумента x, в которых «внешняя» или «внутренняя» функция обращаются в бесконечность или имеют неопределенность.

Методику исследования непрерывности сложной функции

«внутреннюю» u 2x , являющуюся промежуточным аргумен-

ветствует основному аргументу x2 1 (2x 2 x 1).

3. Исследуем поведение «внутренней» функции в окрестности особой точки x1 0 с помощью односторонних пределов.

67

4. Исследуем поведение «внешней» функции и соответственно исходной сложной функции в окрестности точки x1 0. Из

Замечание. Знак «–» при нуле означает, что график функции справа подходит к точке x1 0 снизу. Таким образом, в окрестности точки раз-

Результаты проведенного исследования поведения сложной функции в окрестности точек x1 0 и x2 1 представлены на эс-

кизе (рис. 7.6).

68

7.5.5. Исследовать непрерывность сложных неэлементарных функций, представить эскиз поведения функции в окрестности точек разрыва:

Ответы к задачам темы «Непрерывные и разрывные функции одной действительной переменной»

7.1.1. Функция y f x называется непрерывной в точке x x0 , если для любого как угодно малого числа 0 найдется такое число , что для любого x x0 , x0 x0, x0 выполняется неравенство

f x f x0 .

7.1.2. Нет. 7.1.3. Нет.

7.1.4. а) Любая возрастающая функция; б, в – любая убывающая

lim f x f x0 .

x x0

7.2.1. Точка x2 не является предельной точкой области существования функции.

7.2.2. Число A называется правосторонним (правым) пределом функции y f x в точке x a, если для любого как угодно малого числа 0

найдется такое число , что для любого x a, a все значения функ-

ях предел не существует, в четвертом – существует и равен нулю.

70