m0936

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5.3.2. а) Верно; б) верно; в) верно при условии lim y

5.3.3. а) От противного: пусть lim yn zn A и

lim yn B. Так как

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

7.46 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 293 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

							n		2
					1
	lim		1		1

					n
	n				n
					2

								n
					1
					1
lim		1
lim		1		n
n				n
						3

						n		2 2
			1		2
lim 1			1
lim 1				n
n				n
				2

							n	2 3
			1			3
lim	1		1
lim	1	n
n		n
				3

e4 e10.

e 6

Если	в	последовательности	f n n	lim f n 1,
				n

lim n , то алгоритм преобразования не приводит к неопре-

деленности.

Во многих случаях более удобным представляется другой способ вычисления пределов показательно-степенных функций.

5n 1

Пример. Найти lim

n 7n 3

Решение:

5n 1

n 5

lim

7n 3

n 7

Данный способ можно использовать и в случае неопределен-

ности вида [1 ].

Задачи к разделу 5.6

5.6.1. Вычислить пределы:

sin

а) limn2 sin

; б)

limn sin

; в)

lim n sin

; г)

lim

sin

5.6.2. Вычислить пределы:

										2															1 cos															3
а) lim n tg															; б)						lim				1 cos																			.
а) lim n tg															; б)						lim																			n				.
n										n											n				1 cos															1
																									1 cos															n
5.6.3. Вычислить пределы:																																								n
5.6.3. Вычислить пределы:
					n 2 n																									3n 2 n																												n 2 5
а) lim																		; б) lim																																	; в)					lim									.
n				2n 1																			n										n 1																							n n 1
5.6.4. Вычислить пределы:
									5				n													n 2 n																															n 2						2n 3
а) lim 1																; б) lim																															; в)						lim														;
а) lim 1									n							; б) lim																															; в)						lim														;
n									n													n n 1																															n n 1
									4				n
г) lim 1													.
г) lim 1									n				.
n									n
5.6.5. Вычислить пределы:
				2n2 3n 1 n																																											2n					1				2n 3												lnn 3 log2 n

														2																																			n									; в)					lim										.
а) lim							2n							2		1									; б) lim																				2				n			2						; в)					lim										.
n							2n									1																	n												2							2											n lnn 1
																				Ответы к задачам темы
«Числовые последовательности и их пределы»
5.1.1. а) 1,							1				,		1		,		1		,			1		; б)						1				,				1					,		1			,		1			,	1			; в) 2, 1,							3		,		7	,		4	;
					4							9			16						25									2								4			8								16				32										5				17			13
г) 2, 2,			4		,	2		,					4			; д)					0, 4
			4			2							4															2, 0,16, 0.
																												2, 0,16, 0.
3					3				15																		1				1								1							1							1
5.1.2. а) 1, 4, 7,10,13; б)																											1		,		1				,				1			,				1					,		1		;
5.1.2. а) 1, 4, 7,10,13; б)																													,						,							,			16						,	32			;
																									2					4								8							16							32


в) 1,																				1 1																	,						1 1 1																			;
в) 1,		2, 1 2,																		1 1													2				,						1 1 1																	2		;



г) 1,																			1 4 1 4																	,						1 4 1 4 1 4																			.
г) 1,	2, 1 4 2,																		1 4 1 4													2				,						1 4 1 4 1 4																	2		.
5.1.3. а) 2, 3, 5, 8,13; б) 5,13, 41,121, 365.
5.1.4.а) Монотонно																							убывающая																									ограниченная															последовательность;

б) монотонно убывающая ограниченная последовательность; в) немонотонная ограниченная последовательность; г) немонотонная неограниченная последовательность.

5.1.5. а) Поскольку каждый последующий член последовательности получается из предыдущего прибавлением положительного числа, значит,

последовательность монотонно возрастает. Последовательность представляет собой сумму n первых членов геометрической прогрессии со знаменателем 1/2. Сумма всех членов такой прогрессии равна 2 (школьный курс математики), значит, последовательность ограничена сверху числом 2, снизу – числом 1 (первый, наименьший, член последовательности).

б) Каждый последующий член последовательности больше предыдущего, значит, последовательность монотонно возрастает. Последователь-

ность ограничена снизу числом 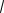2, сверху – числом 2.

5.2.2. Для любой горизонтальной прямой y E найдется номер n E ,

начиная с которого все элементы последовательности окажутся лежащими выше этой прямой.

5.2.3. Числовая последовательность yn имеет предел, равный минус

бесконечности (lim yn ), если при n для любого заранее выбран-

ного как угодно большого по модулю отрицательного числа E 0 найдется такой член последовательности с номером n , что все последующие члены последовательности с номерами n n будут удовлетворять неравенству yn E.

5.2.4. Найдется хотя бы одно число 0, для которого нельзя найти члена последовательности с номером n таким, что все последующие члены последовательности с номерами n n будут находиться внутри интервала A yn A .

5.2.5. Один из самых простых примеров – последовательность 1 n , имеющая точки сгущения 1. Если точек сгущения последовательности больше одной, то последовательность не имеет предела (если предел существует, то он единственный).

5.3.1. Предел последовательности равен –1; корень четной степени и логарифм отрицательного числа в области действительных чисел не определены.

zn yn zn yn , то limzn A B, что противоречит условию. Другое ут-

верждение доказывается аналогично.

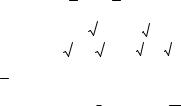
5.3.4. а) Например,

1 1 n

, yn

1 1 n

. Обе последователь-

1 1 n

ности имеют по две предельные точки, значит, расходятся. x

–

постоянная, значит, предел суммы существует;

б)

1 1 n

тогда

0 –

постоянная.

Последова-

тельность сходится;

в)

1 1 n

;

x y

Последовательность схо-

дится;

1 1 n

г)

; zn 1,2,1, 3,1, 4, 1, 5,1, 6, 1, 7,...,

lim

1 1 n

n zn

5.3.5. Нельзя. Пусть

, y

, тогда

lim x

5.4.1. Сумма конечного количества б.б.п. является б.б.п. Произведение конечного количества б.б.п. является б.б.п. Произведение б.б.п. и ограниченной последовательности, все элементы которой, начиная с некоторого номера, положительны, является б.б.п. Произведение б.б.п. и любого положительного числа остается б.б.п.

5.4.2. Например, xn	1	– б.м.п., но	lim	1	.

	n		n xn		1 yn – б.м.п. и
5.4.3. Пусть xn, yn – б.м.п.,			тогда
xn yn xn 1 yn – б.м.п.

5.4.4.а) Например, n n, n n2 ; б) например, n n, n n2 ; в) например, n An, n n.

5.4.5.а) 0; б) 0; в) 0; г) 0. 5.5.1. а) 4; б) 5 ; в) ; г) 0; д) .

	5			2
	1
			2	; в)			1	.
5.5.2. а) 3; б) . 5.5.3. а) 0; б)			2			2	1
5.5.2. а) 3; б) . 5.5.3. а) 0; б)
		2	3		3 2

5.6.1. а) 1; б) 0; в) 2; г) 2 . 5.6.2. а) 2; б) 9. 5.6.3. а) 0; б) ; в) 1.

3 4

5.6.4. а) e5 ; б) e3 ; в) e6 ; г) e 4 . 5.6.5. а) e2 ; б) e 3; в) eln2 .

Требования к практическому усвоению темы «Числовые последовательности и их пределы»

Студент должен знать:

–определение числовой последовательности и способы ее задания; виды последовательностей;

–определения конечного и бесконечного пределов числовой последовательности и их геометрические интерпретации;

–основные свойства сходящихся последовательностей;

–определения бесконечно малых и бесконечно больших последовательностей и их свойства;

–способы вычисления пределов числовых последовательностей с раскрытием неопределенностей;

–использование «замечательных» пределов для раскрытия неопределенностей при вычислении пределов.

Студент должен уметь:

–проверять, имеет ли последовательность заданный предел;

–давать геометрическую интерпретацию предела сходящейся последовательности, строить графики последовательностей;

–вычислять пределы числовых последовательностей с раскрытием неопределенностей, в том числе с использованием «замечательных» пределов.

Тема 6: Пределы функций одной действительной переменной

6.1. Исходные положения

Числовая функция одной действительной переменной величины, как правило, в инженерных задачах является функцией с непрерывным аргументом. Она характеризует соответствие между элементами двух числовых множеств, являющихся подмножествами множества действительных чисел, и обозначается в общем случае y f (x), где x D, D R; y E, E R; D – область существования (определения) функции; E – область значений функции.

Область существования функции одной действительной переменной, как правило, представляется:

– неограниченным интервалом, если все значения перемен-

ной x удовлетворяют неравенству x ;
–	полуограниченным	интервалом	, a	или	b, ,	где
a,b R;
– ограниченным интервалом a, b , где a,b R;
–	полуограниченным	отрезком	, a	или	b, ,	где

a,b R;

–полуинтервалом a, b или a, b , где a,b R;

–отрезком a, b , где a,b R.

Также областью существования могут быть объединения интервалов, полуинтервалов и отрезков, например, a, b c, d ,

, a b, c d, e и т.п.

Если область существования не указана в явном виде, то по умолчанию такой областью считают множество всех числовых значений аргумента, при которых функция имеет смысл на множестве действительных чисел. Такая область существования на-

зывается естественной.

Пример. Найти область существования функции y ln x 1 .

Решение. Логарифм определен только при положительных значениях аргумента, поэтому естественная область существования является решением неравенства x 1 0, т.е. D x| x 1 .

Замечание. Если функция определена не во всей естественной области ее существования, то эту «меньшую» область обязательно указывают в явном виде и обычно называют областью определения.

В математическом анализе функции задаются, как правило, аналитическими выражениями (формулами), хотя возможны и другие способы задания.

1.Табличный способ. Этот способ применяется, как правило,

втом случае, когда область определения X состоит из конечного количества чисел: х1, х2, …, хn. В этом случае в первой строке

таблицы записывают все возможные значения переменной x X, а во второй строке – соответствующие им значения функции: y1, y2, …, yn.

x	x1	x2	x3	…	xn
y	y1	y2	y3	…	yn

2.Графический способ. Этот способ применяется для наглядного рассмотрения зависимости функции от значений ее независимой переменной х.

3.Описательный способ. Этот способ состоит в задании функции с помощью некоторого текста и применяется, как правило, в тех случаях, когда аналитическое задание невозможно или менее наглядно, чем описательное.

Примеры:

1)функция y = [x] – «целая часть х» задается следующим образом: если x = n + r, где x – целое число и 0 r < 1, то [x] = n;

2)функция y = {x} – «дробная часть х» задается следующим образом: если x = n + r, где n – целое число и 0 r < 1, то x r;

3) функция y x (функция Дирихле) равна 1, если число

х– рациональное, и равна 0 в противном случае;

4)функция y x означает число простых натуральных чи-

сел, не превышающих числа х.

4. Аналитический способ. Это наиболее распространенный способ задания функций, предполагающий, что переменные x и y связаны какой-либо формулой (или формулами).

Виды аналитического способа задания функции:

а) явное аналитическое задание функции:

y = x2; y = cos x; y = 2x; y arctg					x 1
					x 1	;	y	x2 6x 8	;
						;	y	x2 6x 8	;
					x 1
		x, если x 0,	1, если x 0,
	x	x, если x 0,		0, если			x 0,
	x		sgnx	0, если			x 0,
		x, если x 0;		1, если			x 0.
				1, если			x 0.

Явное аналитическое задание может осуществляться и в полярной системе координат:

= a ; = 2а(1 + cos ); a

;

2cos2

1 ecos

б) неявное задание функции:

2 2

(x – 2) + (y – 5) = 4; (x

+ y ) = 2a (x

– y

);

1 и т.п.;

в) параметрическое задание функции.

Если линия задана параметрически и является графиком некоторой функции, то можно говорить о том, что данная функция задана параметрически.

x a t sint ,

Например,

y a 1 cost .

Может оказаться, что параметрические уравнения линии задают не одну, а несколько функций. В этом случае также говорят

x acost,	и т.п.
о параметрическом задании функции	и т.п.
y bsint

Одна и та же функция может быть задана различными способами.

Пример.

1) y kx b.

В аналитической геометрии это уравнение прямой на плоскости, в математическом анализе – уравнение линейной функциональной зависимости в явной форме;

2) Ax By C 0 – то же в неявной форме (при условии

B 0);
x x0	mt,
3)	– то же в параметрической форме.
y y0	pt
По аналитическому выражению, как правило, можно постро-
ить график функции.
Графиком функции называется множество таких точек коор-

динатной плоскости, координаты которых удовлетворяют аналитическому выражению функции и условию однозначности.

Согласно условию однозначности в геометрической форме любая прямая, параллельная оси Oy, должна пересекать график

функции не более чем в одной точке.

Функция y f x называется взаимно однозначной, если раз-

ным значениям аргумента соответствуют разные значения функ-

ции: x1 x2 f x1 f x2 .

Многие важные для инженерных приложений функциональные зависимости не удовлетворяют условиям однозначности, и их называют многозначными функциями. В математическом анализе такие функции разбивают, если это возможно, на несколько однозначных функций.

Пример. Окружность, задаваемая уравнением	x2 y2 1,
не является графиком функции, но ее верхняя и нижняя полови-
ны таковыми являются. Таким образом, уравнение x2	y2 1 за-
дает неявно две различные непрерывные функции. Этот факт
можно было установить и аналитически, выразив	из данного

уравнения у: y 1 x2 или y 1 x2 .

Замечание. В классическом математическом анализе функции по умолчанию считаются однозначными. Многозначность функции, как правило, оговаривается особо.

Задачи к разделу 6.1

6.1.1. Проверить, какие из следующих функций являются взаимно однозначными на своей естественной области существования: а) y 2x ; б) y x2 ; в) y x3; г) y lnx; д) y sinx. Привес-

ти другие примеры известных вам однозначных функций, не являющихся взаимно однозначными на своей естественной области существования.

6.1.2.Опираясь на результат предыдущей задачи, сформулировать признак взаимной однозначности функции в геометрической форме.

6.1.3.Сформулировать признак того, что некоторая линия является графиком функции в полярной системе координат.

6.1.4.Найти естественные области существования функций:


а) f x	x 1	; б) f x lg 6x x2 8 ; в) f x tg			1	;

	x 1				x
г) f x arcsin 2x 3 ;
6.1.5. Показать,			что уравнение x2 y2 1 задает не только
пару функций y
			1 x2	, но и другие функции. Учесть, что эти

функции не являются непрерывными.

6.2. Элементарные и неэлементарные функции. Способы составления функций

В математике и ее приложениях важную роль играют элементарные функции, которые можно разделить на следующие виды:

–основные (простейшие),

–составные,

–сложные.

Основными (простейшими) элементарными функциями называют функции, которые нельзя разложить на конечное число других более простых функций:

–постоянная функция y C, C const;

–линейная функция у = х;

– степенная функция y xb при b R;

– показательная функция y ax при a 0, a 1;

– логарифмическая функция y loga x при a 0, a 1;

– тригонометрические функции: y sinx, y cosx, y tg x, y ctg x. Тригонометрические функции являются периодически-

<<< < Предыдущая 1 23 / 293 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.2022619.79 Кб0m0925 (1).pdf
#
15.11.2022619.79 Кб1m0925.pdf
#
15.11.20221.64 Mб4m0927.pdf
#
15.11.20222.37 Mб0m0931.pdf
#
15.11.20224.8 Mб2m0935.pdf
#
15.11.20227.46 Mб2m0936.pdf
#
15.11.20222.25 Mб0m0937.pdf
#
15.11.20221.7 Mб0m0938.pdf
#
15.11.20229.08 Mб1m0939.pdf
#
15.11.20223.68 Mб4m0940.pdf
#
15.11.20221.36 Mб0m0942.pdf