
m0936
.pdf
Пример. Парабола y x 2 2 1 ограничена снизу и име-
ет точную нижнюю грань m 1, которая достигается в точке x 2; сверху парабола не ограничена.
Функция y ex также имеет точную нижнюю грань m 0,
однако нигде не достигает нулевого значения.
Некоторые функции являются не ограниченными как сверху, так и снизу. Например, неограниченными являются основные
|
|
|
|
|
|
|
функции y x3, |
|
|
|
|
|
||
элементарные |
|
y 5 x, |
y tgx, |
y ctgx |
||||||||||
(см. прил. А). |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Задачи к разделу 9.2 |
|
|
|||
|
|
9.2.1. а) Проверить, какие из следующих функций являются |
||||||||||||
четными или нечетными: |
|
|
|
|
|
|||||||||
1) |
y |
|
|
; 2) y 3 |
|
; 3) y x4 5x2 1; 4) y x4 5x3 1; |
||||||||
|
x |
x |
||||||||||||
5) |
y sin Ax, A R; 6) y cos Ax, A R; 7) y tg Ax, A R; |
|||||||||||||
8) |
y arcsinx; |
9) y arccosx; 10) |
y arctgx; |
|
|
|||||||||
11) |
y |
ex e x |
|
(гиперболический синус y shx), прил. Б; |
||||||||||
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
12) |
y |
ex e x |
|
(гиперболический косинус y chx), см. прил. Б; |
||||||||||
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) сформулировать геометрический признак четности и геометрический признак нечетности;
в) сформулировать условие, при котором многочлен будет четной функцией, и условие, при котором многочлен будет нечетной функцией;
г) ответить, может ли функция быть одновременно четной и нечетной;
д) доказать, что любая функция, заданная на симметричном промежутке, может быть представлена в виде суммы четной и нечетной функций. Провести аналогию с гиперболическими синусом и косинусом (см. прил. Б).
9.2.2. а) Доказать, что если T – период функции y f x , то любое число n T, n Z также является периодом этой функции;
121
б) доказать, что если функция y |
f x периодическая, то при |
||||||
некотором |
естественном условии |
(при |
каком?) |
функция |
|||
y g f x также периодическая; |
|
|
|
|
|
||
в) найти наименьший положительный период следующих |
|||||||
функций: 1) |
y sin5x; 2) y sinnx, n N ; 3) |
y sin |
x |
, n N ; |
|||
|
|||||||
|
|
|
|
|
n |
|
|
г) найти наименьший положительный период следующих |
|||||||
функций: 1) |
y x |
– дробная часть х; |
2) y arcsin(sin x); |
||||
3) y 2tgx; 4) sin x ; |
|
|
|
|
|
y x |
|
д) доказать, что |
функции y C |
(постоянная) и |
|||||
(функция Дирихле) являются периодическими, но не имеют наименьшего положительного периода.
9.3.Частные свойства функций
Кчастным относятся свойства функции, которые характеризуют особенности поведения функции в отдельных частях ее области существования (отдельных интервалах, являющихся частями интервала непрерывности функции).
Важными для приложений частными свойствами функций являются знакопостоянство, монотонность, выпуклость.
9.3.1.Знакопостоянство функции
Функция y f x называется знакопостоянной в интервале
a, b , если числовые значения функции сохраняют свой знак при любом значении аргумента х, принадлежащем этому интервалу:
x a, b f x 0 или x a, b f x 0.
Интервал, в котором функция сохраняет свой знак, называется интервалом знакопостоянства. Интервалы знакопостоянства находятся методом интервалов, изучавшимся в средней школе: для этого находится область существования функции y f x ,
затем решается уравнение f x 0. Корни этого уравнения, на-
несенные на область существования, делят ее на интервалы, каждый из которых является интервалом знакопостоянства.
Знак функции в интервале знакопостоянства a, b определя-
ется методом пробных точек. Для этого выбирается координата
122
любой точки xпр a, b и находится знак функции в этой точке
yпр f xпр . |
Этот знак сохраняется во всех внутренних точках |
интервала a, b . |
|
|
9.3.2. Монотонность функции |
Функция |
y f x называется возрастающей на интервале |
a, b , если для любых чисел x1,x2 a, b из условия x1 x2 сле- |
|
дует f x1 f x2 (большему значению аргумента соответствует большее значение функции).
Функция y f x называется убывающей на интервале a, b ,
если для любых чисел |
x1,x2 a, b |
из условия |
x1 x2 |
следует |
|
f x1 f x2 |
(большему значению |
аргумента |
соответствует |
||
меньшее значение функции). |
|
|
|
||
Функция |
y f x |
называется |
монотонной |
на |
интерва- |
ле a, b , если она на всем этом интервале является возрастающей или убывающей.
Возрастание и убывание функций определяют с помощью первых производных.
Теорема (аналитические признаки монотонности).
1. Если в любой точке |
x a, b |
производная |
функции |
|
y f x строго положительна |
f |
|
|
y f x |
x 0 , то функция |
||||
возрастает на интервале a, b . |
x a, b |
|
|
|
2. Если в любой точке |
производная |
функции |
||
y f x строго отрицательна |
f |
|
|
y f x |
x 0 , то функция |
||||
убывает на интервале a, b .
Интервалы, на которых функция только возрастает или толь-
ко убывает, называются интервалами монотонности.
9.3.3. Выпуклость функции
Гладкая кривая называется выпуклой вниз на интервале a, b ,
если касательная, проведенная в любой точке этого интервала, лежит ниже этой кривой (рис. 9.4).
123
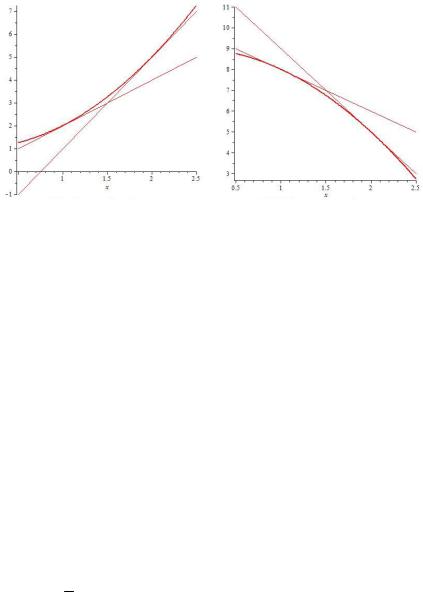
Гладкая кривая называется выпуклой вверх на интервалеa, b , если касательная, проведенная в любой точке этого интервала, лежит выше этой кривой (рис. 9.5).
Рис. 9.4. Выпуклая вниз функция Рис. 9.5. Выпуклая вверх функция
Достаточное условие выпуклости функции вверх или вниз заключается в следующем: график функции y f x имеет на интервале a, b выпуклость вниз, если вторая производная
функции |
во всех точках |
этого |
интервала положительна |
|
f |
|
График функции |
y f x |
имеет на интервале a, b |
x 0 . |
||||
выпуклость вверх, если вторая производная функции во всех точ-
ках этого интервала отрицательна f |
|
|
|
|
|
|
|
|
|
||
x 0 . |
|
|
|
|
|
|
|
|
|||
Задачи к разделу 9.3 |
|
|
|
|
|
|
|
|
|||
9.3.1. Найти промежутки возрастания и убывания функций: |
|||||||||||
а) y |
|
|
|
1 ; г) y e |
|
x2 |
; |
||||
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
д)y x2e x ; е) y ln 6x 8 x2 ; ж) |
|
1 x |
|
|
|
|
|
|
|||
y sinx; з) |
y x cosx; |
|
|
|
|
||||||
9.3.2. Найти промежутки выпуклости вверх и выпуклости |
|||||||||||
вниз функций: |
|
|
|
|
|
|
x2 |
|
|
|
|
а) y 5x 6 x2; б) y x4 13x2 36; в) y |
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
; г) y e 2 |
; |
|
|
|||||||
|
|
|
|
||||||||
д)y x2e x ; е) y ln 6x 8 x2 ; ж) |
1 x2 |
|
|
|
|
|
|
|
|||
y sinx; з) |
y x sinx; |
|
|
|
|
||||||
и) y x 1. x
124
9.4. Локальные свойства функций
Локальные свойства функции характеризуют особенности поведения функции в отдельных характерных точках области существования функции и их окрестностях.
9.4.1. Нули функции
Нули функции y f x – это значения ее аргумента, при ко-
торых она обращается в ноль.
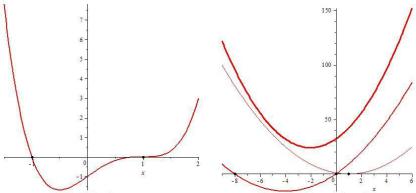
Нули функции определяются как решения уравнения f x 0. С геометрической точки зрения нули функции – это точки пересечения или касания (или того и другого) графика функции с осью абсцисс (рис. 9.6).
Функция может не иметь нулей. Такова, например, показа-
тельная функция y ax (см. прил. А). Квадратичная функция y ax2 bx c может иметь или не иметь нули в зависимости от знака дискриминанта D b2 4ac (рис. 9.7). Нулевые точки разделяют интервалы непрерывности на интервалы знакопостоянства.
Рис. 9.6. Нули функции |
Рис. 9.7. Нули квадратичных функций |
9.4.2. Экстремумы функции
Важнейшим локальным свойством функции является наличие у нее экстремумов.
Функция y f x имеет максимум в точке x0 , если найдется число 0 такое, что для всех значений x x0 , x0 , x x0 имеет место неравенство f x0 f x .
125
Функция y f x имеет минимум в точке x0 , если найдется
число 0 такое, что для всех значений x x0 , x0 , x x0 имеет место неравенство f x0 f x .
Точкой экстремума функции y f x называется ее точка максимума или точка минимума x0 .
Экстремумы возможны только в точках (критические точки первого рода), в которых первая производная функции равна нулю, бесконечности или не существует. Если непрерывная функция y f x является гладкой, то критические точки первого рода определяются как корни уравнения f x 0 (точки стацио-
нарности).
Наличие у гладкой функции точек стационарности является необходимым (но не достачным) условием наличия экстремумов.
Теорема Ферма (необходимое условие наличия экстрему-
мов). Если функция y f x имеет на промежутке a, b непрерывную производную и в точке c a, b локальный экстремум, то f c 0.
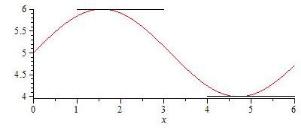
Геометрический смысл теоремы Ферма заключается в том, что в точках экстремума гладкой функции касательная параллельна оси абсцисс (рис. 9.8).
Рис. 9.8. Геометрический смысл теоремы Ферма
Окончательный вывод об экстремумах можно сделать только при выполнении достаточного условия наличия экстремума.
Первое достаточное условие экстремума: если при переходе через критическую точку x0 первая производная:
– меняет знак с положительного на отрицательный, то точка x0 является точкой максимума;
126
–меняет знак с отрицательного на положительный, то точка x0 является точкой минимума;
–не меняет свой знак, то экстремума в точке x0 нет.
При практическом определении экстремумов с помощью первого достаточного условия используют метод интервалов: для этого находится область существования производной y f x ,
затем решается уравнение f x 0. Корни этого уравнения, на-
несенные на область существования, делят ее на интервалы, каждый из которых является интервалом знакопостоянства производной.
Знак производной в интервале знакопостоянства a, b опре-
деляется методом пробных точек. Для этого выбирается коорди-
ната любой точки xпр a, b |
и находится знак производной в |
|||||||
этой точке |
f xпр . |
Этот знак сохраняется во всех внутренних |
||||||
точках интервала a, b . |
|
|
|
|
|
|||
|
|
|
|
|
Второе |
достаточное условие |
||
|
|
|
|
экстремума: в точке стационарности |
||||
|
|
|
|
x0 |
функция |
имеет максимум, |
если |
|
|
|
|
|
f x0 0, |
и |
минимум, |
если |
|
|
|
|
|
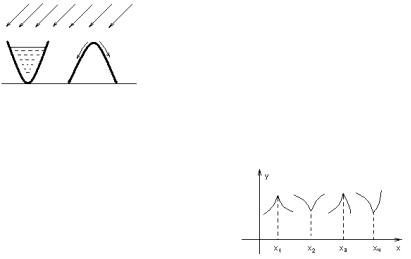
f x0 0. Для лучшего запоминания |
||||
Рис. 9.9. «Правило дождя» |
второго достаточного условия исполь- |
|||||||
|
|
|
|
зуют мнемоническое «правило дождя» |
||||
|
|
|
|
(рис. 9.9). |
|
|
|
|
В общем случае в критических |
|
|
|
|||||
точках первая |
производная |
может |
|
|
|
|||
быть равна бесконечности или не |
|
|
|
|||||
существовать. Эти точки являются |
|
|
|
|||||
особыми |
точками |
непрерывной |
|
|
|
|||
функции (см. раздел 8.1), в них воз- |
|
Рис. 9.10. «Острые» |
|
|||||
можно существование «острых» экс- |
|
|
||||||
тремумов (рис. 9.10). |
|
|
|
экстремумы |
|
|||
Достаточное |
условие |
существо- |
|
|
|
|||
вания «острых» экстремумов основано на использовании одно-
127
сторонних производных: если в критической точке x0 левая про-
изводная положительна, а правая отрицательна, то x0 – точка максимума; если левая производная отрицательна, а правая положительна, то x0 – точка минимума.
Пример. Определить экстремумы функций: а) y 3 x 1,
x 1,
б)y 3
 x 1 2 .
x 1 2 .
Решение.
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а) y 3 |
x 1 |
|
|
|
|
|
. Производная не равна нулю ни |
|||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
3 3 x 1 2 |
|
|
|
|
|
|
|
|||||
при каких значениях |
аргумента, но |
при |
x0 1 производная |
|||||||||||||||||
|
|
|
|
|
|
|
1 возможен «острый» экстремум, ни в ка- |
|||||||||||||
y 1 . В точке x0 |
||||||||||||||||||||
кой другой точке экстремума быть не может. |
|
|
||||||||||||||||||
В точке |
|
x0 1 |
|
и |
левая и |
правая |
производные функции |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
1 |
|
|
|
y 3 x 1 положительны, так как |
|
|
|
0 при любом |
||||||||||||||||
3 3 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 2 |
||||
значении |
аргумента. |
Из достаточного |
условия существования |
|||||||||||||||||
«острых» экстремумов следует, что в точке |
x0 1 экстремума |
|||||||||||||||||||
нет. График функции представлен на рис. 9.11. |
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) y |
|
|
x 1 |
|
|
3 3 x 1. |
Экстремумы функций опреде- |
|||||||||||||
|
|
|||||||||||||||||||
ляются аналогично а. Если экстремум есть, то только в точке x0 1.
При x 1 производная от-
рицательна: |
|
2 |
0, а при |
|
|
|
|
|
|
||
3 3 |
|
x 1 |
|
||
|
|
|
|
||
x 1 – положительна, поэтому |
|
||||
в соответствии с достаточным |
|
||||
условием существования «ост- |
|
||||
рого» экстремума x0 1 – точ- |
|
||||
ка минимума. График функции Рис. 9.11. График функции y 3 |
x 1 |
||||
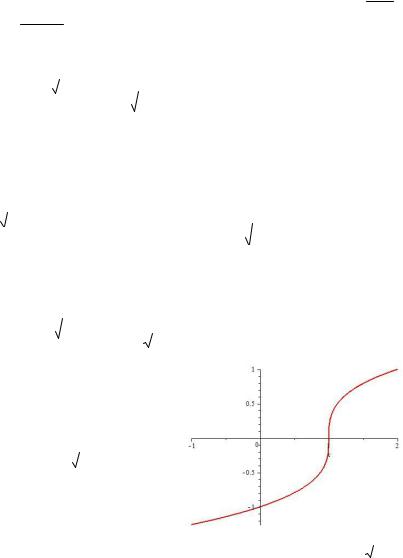
представлен на рис. 9.12.
128

Рис. 9.12. График функции y 3 x 1 2
x 1 2
9.4.3. Перегибы функции
Если точка x0 принадлежит области определения функции y f x и слева от этой точки функция выпукла, а справа вогну-
та (или наоборот: слева вогнута, а справа выпукла), то точка x0
называется точкой перегиба.
В точках перегиба вторая производная функции равна нулю, бесконечности или не существует. В случае гладкой функции необходимое условие перегиба имеет вид: f x 0. Корни этого уравнения являются критическими точками второго рода, в которых возможны перегибы функции. Окончательно вопрос о наличии перегиба функции решают, используя достаточное условие существования точки перегиба: если вторая производная f x в
окрестности критической точки x0 имеет различные знаки справа и слева от x0 , то эта точка является точкой перегиба (рис. 9.13).
Рис. 9.13. Точка перегиба
129
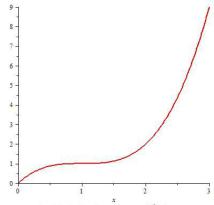
Пример. Найти точку перегиба функции y x 1 3 1,
построить график функции.
Решение.
1.Определяем координаты критических точек. y x 1 3 1 3 x 1 2 , y 6 x 1 x0 1.
2.Проверяем, является ли
точка x0 1 точкой перегиба. |
|
|||||
При |
x 1 |
вторая произ- |
|
|||
водная |
y 6 x 1 0, |
при |
|
|||
x 1 – y 6 x 1 0, значит, |
|
|||||
x0 1 – точка перегиба. |
|
|
||||
3. Строим |
график функ- |
|
||||
ции y x 1 3 |
1. |
Поскольку |
|
|||
y 1 x 1 3, |
то |
графиком |
|
|||
функции является кубическая |
|
|||||
парабола, смещенная на еди- |
Рис. 9.14. График функции |
|||||
ницу вправо |
и на единицу |
|||||
y = (x – 1)3 + 1 |
||||||
вверх (рис. 9.14). |
|
|
||||
|
|
|
||||
|
9.4.4. Наибольшее и наименьшее значения функции |
|||||
Для непрерывных на отрезке a, b функций справедлива |
||||||
теорема Вейерштрасса: |
если функция y f x непрерывна на |
|||||
отрезке a, b , то она достигает на этом отрезке наибольшего и наименьшего значений.
Наибольшее и наименьшее значения функции могут достигаться либо в точках экстремумов, либо на концах отрезка a, b
(рис. 9.15). Алгоритм нахождения наибольшего и наименьшего значений состоит в следующем:
1. Находим первую производную y функции y f x , опре-
деляем критические точки, принадлежащие интервалу a, b .
2. Определяем значения функции в критических точках и на концах отрезка f a , f b .
130
