Физика для бакалавра Часть 2

Мы видим, что чем больше масса частицы, тем меньше неопределенности ее координаты и скорости и, следовательно, с тем большей точностью применимо понятие траектории. Уже для макрочастицы размером всего 1 мкм неопределенности значений х и vx оказываются за пределами точности измерения этих величин, так что практически ее движение будет неотличимо от движения по траектории.

При определенных условиях даже движение микрочастицы может приближенно рассматриваться как происходящее по траектории. Например, движение электрона в электронно-лучевой трубке.

Соотношение неопределенности является одним из фундаментальных положений квантовой механики. Одного этого соотношения достаточно, чтобы получить ряд важных результатов. В частности оно позволяет объяснить тот факт, что электрон не падает на ядро атома, а также оценить размеры простейшего атома и минимальную возможную энергию электрона в таком атоме.

Соотношение неопределенностей неоднократно являлось предметом философских дискуссий, приводивших некоторых философов к его неправильному истолкованию. Например, по их мнению, соотношение неопределенностей, не давая возможности одновременно точно определить координаты и импульсы (скорости) частиц, устанавливает границу познаваемости мира, с одной стороны, и существование микрообъектов вне пространства и времени – с другой. На самом деле соотношение неопределенностей не ставит какого-либо предела познанию микромира, а только указывает, насколько применимы к нему понятия классической механики.

29.5. Волновая функция, ее статистический смысл

Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микрообъектам, диктуемая соотношением неопределенностей, а также противо-

281

речие целого ряда экспериментов с применяемыми в начале XX века теориями привели к новому этапу развития квантовой теории – созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств. Ее создание и развитие охватывает период с 1900 года (формулировка Планком квантовой гипотезы) до 20-х годов XX века. Оно связано прежде всего с работами австрийского физика Э. Шредингера (1887–1961), немецкого физика В. Гейзенберга и английского физика П. Дирака (1902–1984).

На данном этапе развития возникли новые принципиальные проблемы, в частности проблема физической природы волн де Бройля. Для выяснения этой проблемы сравним дифракцию световых волн и микрочастиц.

1. Дифракционная картина, наблюдаемая для световых волн, характеризуется тем, что в результате наложения дифрагирующих волн друг на друга в различных точках пространства происходит усиление или ослабление амплитуды колебаний. Согласно волновым представлениям о природе света, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны. По представлениям фотонной теории, интенсивность определяется числом фотонов, попадающих в данную точку дифракционной картины. Следовательно, число фотонов в данной точке дифракционной картины задается квадратом амплитуды световой волны, в то время как для одного фотона квадрат амплитуды определяет вероятность попадания фотона в ту или иную точку.

2. Дифракционная картина, наблюдаемая для микрочастиц, также характеризуется неодинаковым распределением потоков микрочастиц, рассеянных или отраженных по различным направлениям, – в одних направлениях наблюдается большее число частиц, чем в других. Наличие максимумов в дифракционной картине с точки зрения волновой теории означает, что эти направления соответствуют наибольшей интенсивности волн де Бройля. С другой стороны, интенсивность волн де Бройля ока-

282

зывается больше там, где имеется большее число частиц, т.е. интенсивность волн де Бройля в данной точке пространства определяет число частиц, попавших в эту точку. Таким образом, дифракционная картина для микрочастиц есть проявление статистической (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая.

Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории. Можно ли волны де Бройля истолковывать как волны вероятности, т.е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.

Чтобы устранить эти трудности, немецкий физик М. Борн в 1926 году предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая ψ (х, у, z, t). Эту величину называют также волновой функцией (или ψ-функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:

где ψ2 =ψψ*,ψ* – функция, комплексно сопряженная с ψ.

Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени t в области с координатами х и x + dx, у и y + dy, z и z + dz.

Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому – с помощью волновой функ-

283

ции, которая является основным носителем информации об их корпускулярных и волновых свойствах. В элементе объемом dV вероятность нахождения частицы

(квадрат модуля ψ-функции) имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z.

Таким образом, физический смысл имеет не сама ψ-функ- ция, а квадрат ее модуля ψ 2 , которым задается интенсивность

волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V (согласно теореме сложения вероятностей)

W = dW = ψ 2 dV.

V V

Поскольку ψ 2 dV определяется как вероятность, необхо-

димо волновую функцию ψ нормировать так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятно-

стей

−∞

где данный интеграл (29.12) вычисляется по всему бесконечному пространству, т.е. по координатам х, у, z от −∞ до ∞ . Таким образом, условие (29.12) говорит об объективном существовании частицы во времени и пространстве.

284

Чтобы волновая функция являлась объективной характеристикой состояния микрочастиц, она должна удовлетворять ряду ограничительных условий.

Функция W, характеризуя вероятность обнаружения действия микрочастицы в элементе объема, должна быть:

–конечной (вероятность не может быть больше единицы),

–однозначной (вероятность не может быть неоднозначной величиной),

–непрерывной (вероятность не может изменяться скачком). Волновая функция удовлетворяет принципу суперпозиции:

если система может находиться в различных состояниях, описываемых волновыми функциями Ψ1,Ψ2 ,Ψ3 ,...,Ψn ,..., то она

также может находиться в состоянии Ψ, описываемом линейной комбинацией этих функций:

Ψ = CnΨ n ,

n

где Сп (n = 1,2,...) – произвольные, вообще говоря, комплексные числа. Сложение волновых функций (амплитуд вероятностей), а не вероятностей (определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.

Волновая функция Ψ, являясь основной характеристикой состояния микрообъектов, позволяет в квантовой механике вычислять средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние <r> электрона от ядра вычисляют по формуле

∞

< r >= r Ψ 2 dV ,

−∞

где интегрирование производится, как и в случае (29.12).

285

29.6. Уравнение Шредингера

Статистическое толкование волн де Бройля и соотношение неопределенностей Гейзенберга привели к выводу, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции Ψ(х, у, z, t), так как именно она,

точнее, величина Ψ 2 определяет вероятность пребывания час-

тицы в момент времени t в объеме dV, т.е. в области с координатами х и x+dx, у и y+dy, z и z + dz. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему электромагнитные волны.

Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 году Э. Шредингером. Уравнение Шредингера, как и все основные уравнения физики (например, уравнения Ньютона в классической механике и уравнения Максвелла для электромагнитного поля), не выводится, а постулируется. Правильность этого уравнения подтверждается согласием с опытом получаемых с его помощью результатов, что, в свою очередь, придает ему характер закона природы. Уравнение Шредингера имеет вид

где i – мнимая единица; U (х, у, z, t) – потенциальная функция частицы в силовом поле, в котором она движется; ψ(х, у, z, t) – искомая волновая функция частицы.

Уравнение (29.13) называется уравнением Шредингера в общем виде. И оно справедливо для любой частицы (со спином, равным 0), движущейся с малой (по сравнению со скоростью света) скоростью, т.е. со скоростью v << c. Его также называют уравнением Шредингера, зависящим от времени. Оно дополняетсяусловиями, накладываемыминаволновуюфункцию:

1)волновая функция должна быть конечной, однозначной

инепрерывной;

2)производные ∂ψ∂x , ∂ψ∂y , ∂ψ∂z , ∂ψ∂t должны быть непре-

рывны; 3) функция ψ 2 должна быть интегрируема; это условие

в простейших случаях сводится к условию нормировки вероят-

ностей (29.12).

Для многих физических явлений, происходящих в микромире, уравнение (29.13) можно упростить, исключив зависимость ψ от времени, иными словами, найти уравнение Шредин-

гера для стационарных состояний – состояний с фиксированными значениями энергии. Это возможно, если силовое поле, вкотором частица движется, стационарно, т.е. функция U = U (х, у, z) не зависит явно от времени и имеет смысл потенциальной энергии. В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая – только времени, причем зависимость от времени выражается множителем

e−iωt = e−i E t , так что

где Е – полная энергия частицы, постоянная в случае стационарного поля. Подставляя (29.14) в (29.13), получим

−i E t

откуда после деления на общий множитель e и соответствующих преобразований придем к уравнению, определяющему функцию ψ:

Уравнение (29.15) называется уравнением Шредингера для стационарных состояний. В это уравнение в качестве параметра входит полная энергия Е частицы. В теории дифференциальных уравнений доказывается, что подобные уравнения имеют бесчисленное множество решений, из которых посредством наложения граничных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: волновые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким образом,

реальный физический смысл имеют только такие решения, которые выражаются регулярными функциями ψ. Но регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном, или сплошном, спектре, во втором – о дискретном спектре.

288

29.7. Квантовая частица в одномерной «потенциальной яме»

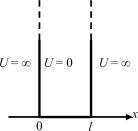
Рассмотрим, в качестве примера, решения уравнения Шредингера, описывающие движения частиц, находящихся в одно-

мерной прямоугольной «потенциальной яме» с бесконечно высо-

где l – ширина «ямы», а энергия отсчитывается от ее дна

(см. рис. 29.3).

Уравнение Шредингера (29.15) для стационарных состояний в случае одномерной задачи запишется в виде

По условию задачи (бесконечно высокие «стенки») частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х = 0 и х = l) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид

289

Общее решение дифференциального уравнения (29.18):

ψ(x) = Asin kx + B cos kx,

так как по (29.17) ψ(0) = 0, то В = 0. Тогда

Условие ψ(l) =A sin kl = 0 (29.17) выполняется только при kl = = nπ, где п – целые числа, т.е. необходимо, чтобы

т.е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Еп, зависящих от целого числа п. Следовательно, энергия En частицы в «потенциальной яме» с бесконечно высокими «стенка-

290