Физика. Ч. II Основы электромагнетизма учебное пособие

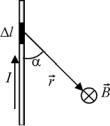
Пусть по проводнику течет ток I . Вычислим магнитное поле, создаваемое

малым элементом тока l (рис. 3.9). Если v средняя скорость упорядоченного движения электронов, тогда согласно уравнению (3.11, а) магнитное поле, создаваемое в точке наблюдения одним электроном из элемента тока:

B1 0 ev sin . 4 r2

Все свободные электроны элемента тока создают поля, направленные за плоскость чертежа (см. рис. 3.9), поэтому по принципу суперпозиции величина суммарного поля элемента тока: B NB1 , где N число свободных элек-

тронов в элементе проводника l . Величину N можно выразить через концентрацию свободных электронов: N nV nS l , где V объем элемента проводника, S сечение проводника. Таким образом:

Уравнение (3.12) определяет магнитное поле, создаваемое элементом тока, и представляет собой закон Био – Савара – Лапласа. Оно было впервые получено французскими физиками Био и Саваром на основании экспериментального материала при содействии математика Лапласа.

131

Закон Био – Савара – Лапласа можно записать в дифференциальной форме (переходя от малого к бесконечно малому элементу тока l dl ):

Рассмотрим примеры расчета магнитных полей при помощи закона Био – Савара – Лапласа.

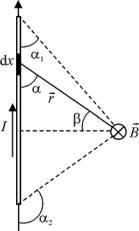
Пример 3.3. Поле прямого тока. Найти магнитное,

создаваемое прямолинейным отрезком провода с током I в произвольной точке пространства.

Решение. Зададим положение точки наблюдения при помощи углов 1 , 2 и расстояния R от точки наблюдения

до проводника (рис. 3.10). Разобьем весь отрезок провода на малые элементы длины dx . Поле одного малого элемента dx с координатой x определяется со-

132

тематики: проинтегрировать уравнение (3.12, а). Для этого в уравнении (3.12) нужно перейти к одной переменной величине (переменной интегрирования). Удобнее всего в качестве переменной интегрирования взять угол (рис. 3.10). Вы-

разим все переменные величины в уравнении (3.12) через .

Во-первых, sin sin 90 cos . Далее, tg x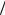R .

Берем дифференциалы от обеих частей этого равенства: d tg R1 dx cosdβ2β R1 dx dx cosRd2 .

Таким образом, для поля элемента dx получим:

Осталось выразить через переменную r : r R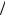cos . Следовательно

dB 0 I cos d . 4 R

Теперь интегрируем, учитывая, что все элементы находятся в пределах углов от 1 (крайний нижний элемент) до 2 (крайний верхний элемент):

133

Частным случаем формулы (3.13) является поле бесконечно длинного прямого провода на расстоянии R от него

( 1 0 , 2 180 ):

Пример 3.4. Магнитное поле в центре кругового то-

ка. Найти магнитную индукцию, создаваемую круговым витком радиуса R с током I в центре витка.

Решение. Разобьем виток на малые элементы dl (рис. 3.11). Длину каждого элемента выразим через радиус витка R и соответствующий центральный угол d :

Пример 3.5. Магнитное поле на оси кругового тока.

Найти магнитную индукцию, создаваемую круговым витком радиуса R с током I в произвольной точке на оси витка.

134

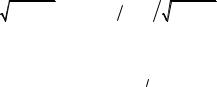
Решение. Разобьем виток на малые элементы dl (рис. 3.11). Длину каждого элемента выражаем через радиус витка R и соответствующий центральный угол d : dl Rd . Согласно уравнению (3.12, а) магнитное по-

ле, создаваемое одним элементом тока в некоторой точке на оси витка, удаленной на расстояние y от центра витка

( 90 ):

суммировать модули векторов dB нельзя.

Поскольку результирующий вектор B будет направлен вдоль оси y , он представляет собой сумму про-

135

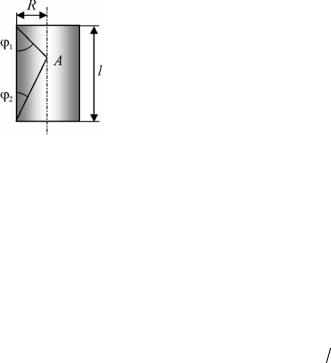
Используя результат примера 3.5, можно определить магнитное поле на оси соленоида – катушки с током. Предлагаем читателям самостоятельно поупражняться с интегрированием и приведем лишь ответ для поля в произвольной

токов, текущих по некоторым поверхностям. Поверхностная плотность тока это сила тока, приходящаяся на единицу длины отрезка, перпендикулярного направлению тока. В нашем случае можно считать, что ток идет по боковой поверхности соленоида. Пусть соленоид имеет длину l , состоит из N витков, и по его обмотке течет ток I . Тогда полный ток, текущий по боковой поверхности соленоида,

В случае, когда длина соленоида намного превосходит его радиус ( 1 0 , 2 0 ),

Формула (3.18) еще будет выведена в дальнейшем с помощью теоремы о циркуляции для магнитного поля. Будет показано, что магнитное поле внутри «длинных» соленоидов однородно и, что формулу (3.18) можно использовать для расчета поля в любой точке внутри соленоида, а не только на его оси.

136

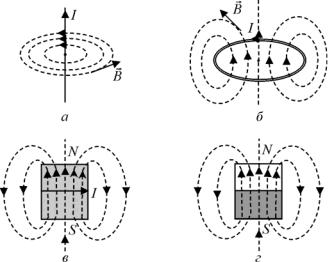
На рис. 3.13 показаны силовые линии магнитных полей прямого провода, витка с током, соленоида и полосового магнита.

Рис. 3.13. Картина силовых линий магнитных полей: а – прямого проводника; б – витка; в – соленоида; г – полосового магнита

Обратим внимание на то, что силовые линии магнитного поля всегда замкнуты. Вектор магнитной индукции направлен по касательной к линиям (рис. 3.13, а, б) в сторону, указываемую направлением стрелки на силовой линии.

В случае прямого тока (рис. 3.13, а) силовые линии представляют собой коаксиальные окружности с центрами на оси тока. Направление магнитной индукции в любой точке можно определить из закона Био – Савара – Лапласа, записанного в векторном виде (формула (3.12, б)). Кроме того, для определения направлений силовых линий существует простое правило, называемое правилом буравчика или правого винта: при вращении буравчика в направлении силовых линий его поступательное движение совпадает с направлением тока.

137

В случае витка с током (рис. 3.13, б) или соленоида (рис. 3.13, в) направление магнитной индукции на оси витка или соленоида тоже можно определить по правилу буравчика. Направление магнитной индукции совпадает с направлением поступательного движения буравчика при его вращении по току.

Отметим, что картина силовых линий магнитного поля соленоида абсолютно идентична картине силовых линий полосового магнита (рис. 3.13, г). Концы соленоида тоже называют северным и южным полюсами. Силовые магнитные линии во внешнем пространстве соленоида или магнита идут от северного полюса к южному, а во внутреннем пространстве – наоборот.

3.7. Циркуляция и поток вектора магнитной индукции

Циркуляция и поток вектора магнитной индукции (как и любого вектора вообще) определяются так же, как и для вектора напряженности электрического поля.

Циркуляцией по отрезку прямой l однородного по-

ля B называется скалярное произведение: B,l Bl cos ,

где угол между векторами B и l .

Рассмотрим участок L произвольной направленной

кривой. Разобьем этот участок на мелкие отрезки l , направленные так же, как и сама кривая. Тогда циркуляцией

вектора B по участку кривой L называется криволинейный интеграл B, dl , который представляет собой предел

L

суммы при делении кривой на бесконечно малые отрезки:

138

Малый участок кривой можно считать прямым отрезком, а поле Bi в пределах этого участка однородным, по-

этому каждое слагаемое в сумме Bi , li представляет со-

бой циркуляцию вектора Bi по отрезку li .

Циркуляцию вектора B по замкнутой кривой будем обозначать как (B,dl ) .

L

Магнитным потоком Ф вектора B в однородном поле через плоскую поверхность площади S называется величина

угол между направлением вектора B и направлением нормали к поверхности. В системе СИ единица измерения магнитного потока – вебер (Вб).

Теперь рассмотрим участок произвольной поверхно-

сти S . Потоком вектора B через участок поверхности S называется поверхностный интеграл, представляющий собой предел суммы при делении поверхности на куски Si

а поле Bi в пределах этого участка – однородным, поэтому каждое слагаемое в сумме Bi ,ni Si представляет собой поток вектора Bi через плоскую поверхность Si .

139

Поток вектора B через замкнутую поверхность будем обозначать как B,n dS .

S

Сформулируем две теоремы о циркуляции и потоке вектора магнитной индукции.

Теорема о циркуляции вектора магнитной индукции

(для поля в вакууме). Циркуляция вектора магнитной индукции по произвольному замкнутому направленному контуру:

произвольную поверхность, натянутую на контур, по которому вычисляется циркуляция. Направление обхода контура и направление нормали к натянутой на него поверхности связаны правилом буравчика. Если ток идет по направлению нормали, то его следует считать положительным, если наоборот – отрицательным.

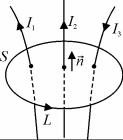
Например, циркуляция вектора магнитной индукции по контуру L , изображенному на рис. 3.14, рав-

на 0 I1 I2 I3 .

140