Физика. Ч. II Основы электромагнетизма учебное пособие

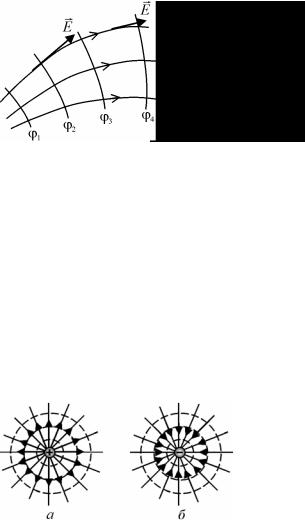
поля (рис. 1.5). Густота силовых линий (число силовых линий, проходящих через единицу площади) пропорциональна напряженности электрического поля.

Эквипотенциальные поверхности (эквипотенциали) –

поверхности равного потенциала. Это поверхности (линии), при движении по которым потенциал не меняется. Иначе, разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю. Силовые линии перпендикулярны эквипотенциальным

поверхностям и направлены в сторону наиболее резкого убывания потенциала. Этот факт следует из уравнения (1.10) и доказывается в курсе математического анализа в разделе «Скалярные и векторные поля».

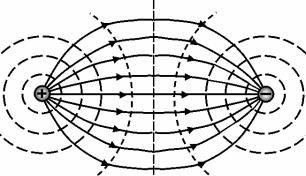
Рассмотрим в качестве примера электрическое поле, создаваемое на расстоянии r от точечного заряда. Согласно (1.11, б) вектор напряженности совпадает с направлением вектора r , если заряд положительный, и противоположен ему, если заряд отрицательный. Следовательно, силовые линии расходятся радиально от заряда (рис. 1.6, а, б).

Рис. 1.6. Электрические поля:

а– положительного заряда;

б– отрицательного заряда

21

Густота силовых линий, как и напряженность, обратно

пропорциональна квадрату расстояния ( r 2 ) до заряда. Эквипотенциальные поверхности электрического поля точечного заряда представляют собой сферы с центром в месте расположения заряда.

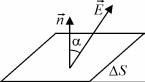
На рис. 1.7 показано электрическое поле системы двух равных по модулю, но противоположных по знаку точечных зарядов. Мы предоставляем рассмотреть этот при-

Рис. 1.7. Электрическое поле двух равных по модулю и противоположных по знаку точечных зарядов

мер читателям самостоятельно. Отметим лишь, что силовые линии всегда начинаются на положительных зарядах и заканчиваются на отрицательных. В случае электрического поля одного точечного заряда (рис. 1.6, а, б) предполагается, что силовые линии обрываются на очень удаленных зарядах противоположного знака. Считается, что Вселенная в целом нейтральна. Поэтому, если имеется заряд одного знака, то где-то обязательно найдется равный ему по модулю заряд другого знака.

22

1.6.Теорема Гаусса для электрического поля

ввакууме

Основной задачей электростатики является задача о нахождении напряженности и потенциала электрического поля в каждой точке пространства. В подраздел 1.4 мы решили задачу о поле точечного заряда, а также рассмотрели поле системы точечных зарядов. В этом подразделе речь пойдет о теореме, позволяющей рассчитывать электрическое поле более сложных заряженных объектов. Например, заряженной длинной нити (прямой), заряженной плоскости, заряженной сферы и др. Рассчитав напряженность электрического поля в каждой точке пространства, используя уравнения (1.12) и (1.13), можно вычислить потенциал в каждой точке или разность потенциалов между двумя любыми точками, т.е. решить основную задачу электростатики.

Для математического описания введем понятие потока вектора напряженности, или потока электрического по-

ля. Потоком вектора Е электрического поля через плоскую поверхность площади S называется величина

где E – напряженность электрического поля, которая предполагается постоянной в пределах площадки S ; – угол

между направлением вектора E и единичного вектора нормали n к площадке S (рис. 1.8).

Формулу (1.16) можно записать, используя понятие скалярного произведения векторов:

Ф E,n S . (1.15, а) Рис. 1.8. Расчетная схема

23

В случае, когда поверхность S не плоская, для вычисления потока ее необходимо разделить на малые части Si ,

которые можно приблизительно считать плоскими, а затем записать выражение (1.16) или (1.16, а) для каждого куска поверхности и сложить их. В пределе, когда поверхность Si очень мала ( Si 0 ), такую сумму называют поверхност-

ным интегралом и обозначают E, n dS . Таким образом,

S

поток вектора напряженности электрического поля через произвольную поверхность S определяется выражением

В качестве примера рассмотрим сферу радиуса r, центром которой служит положительный точечный заряд q ,

иопределим поток электрического поля через поверхность этой сферы. Силовые линии (см., например, рис. 1.6, а) выходящие из заряда, перпендикулярны поверхности сферы,

ив каждой точке сферы модуль напряженности поля один

итот же:

Е k rq2 4 q0r2 .

Площадь сферы S 4 r2 , тогда

Величина ES и представляет собой поток электрического поля через поверхность сферы. Таким образом, получаем Ф q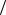 0 . Видно, что поток через поверхность сферы

электрического поля не зависит от радиуса сферы, а зависит только от самого заряда q . Поэтому, если провести ряд

концентрических сфер, то поток электрического поля через

24

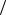
все эти сферы будет одинаковым. Очевидно, что число силовых линий, пересекающих эти сферы, тоже будет одинаковым. Условились число силовых линий, выходящих из заряда, принимать равным потоку электрического поля:

N ES q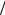 0 .

Если сферу заменить любой другой замкнутой поверхностью, то поток электрического поля и число силовых линий, пересекающих ее, не изменятся. Кроме того, поток электрического поля через замкнутую поверхность, а значит и число силовых линий, пронизывающих эту поверхность, равняется q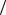 0 не только для поля точечного заряда,

но и для поля, создаваемого любой совокупностью точечных зарядов, в частности – заряженным телом. Тогда величину q следует считать как алгебраическую сумму всех

зарядов, находящихся внутри замкнутой поверхности. В этом и состоит суть теоремы Гаусса, которая формулируется так:

Поток вектора напряженности электрического поля через произвольную замкнутую поверхность равняет-

разуя первый интеграл, мы сначала воспользовались тем, что

25

векторы E и n параллельны, а значит E, n E cos0 E .

Затем вынесли величину E за знак интеграла в силу того, что она постоянна в любой точке сферы S . Применяя теорему Гаусса для решения конкретных задач, специально

вкачестве произвольной замкнутой поверхности стараются выбирать поверхность, для которой выполняются описанные выше условия.

Приведем несколько примеров на применение теоремы Гаусса.

Пример 1.2. Рассчитать напряженность электрического поля равномерно заряженной бесконечной нити. Определить разность потенциалов между двумя точками

втаком поле.

Решение. Предположим для определенности, что нить заряжена положительно. В силу симметрии задачи можно утверждать, что силовые линии будут радиально расходящимися от оси нити прямыми (рис. 1.9), густота которых по мере удаления от нити уменьшается по какому-то закону. По этому же закону будет уменьшаться и величина электрического

поля E . Эквипотенциальными поверхностями будут цилиндрические поверхности с осью, совпадающей с нитью.

Пусть заряд единицы длины нити равен . Эта величина называется линейной плотностью заряда и измеряется в СИ в Кл/м. Для расчета напряженности

поля применим теорему Гаусса. Для этого в качестве произвольной замкнутой поверхности S выберем цилиндр радиуса r и длины l , ось которого совпадает с нитью (см. рис. 1.9). Вычислим поток электрического поля через

26

площадь поверхности цилиндра. Полный поток складывается из потока через боковую поверхность цилиндра и потока через основания

Однако Фосн 0 , поскольку в любой точке на основаниях цилиндра Е n . Это значит, что E,n 0 в этих точках. Поток через боковую поверхность Фбок ESбок .

т.е. напряженность и густота силовых линий электрического поля равномерно заряженной бесконечной нити убывает

обратно пропорционально расстоянию ( r 1 ).

Найдем разность потенциалов между точками, находящимися на расстояниях r1 и r2 от нити (принадлежащими эквипотенциальным цилиндрическим поверхностям с радиусами r1 и r2 ). Для этого воспользуемся связью напряженно-

27

сти электрического поля с потенциалом в виде (1.9, в): Еr d dr . Учитывая выражение (1.19), получим дифференциальное уравнение с разделяющимися переменными:

Пример 1.3. Рассчитать напряженность электрического поля равномерно заряженной плоскости. Определить разность потенциалов между двумя точками в таком поле.

Решение. Электрическое поле равномерно заряженной плоскости показано на рис. 1.10. В силу симметрии силовые линии должны быть перпендикулярны плоскости. Поэтому

сти. Пусть заряд единицы площади плоскости равен . Эта величина называется поверхностной плотностью заряда и измеряется в СИ в Кл/м2.

Применим теорему Гаусса. Для этого в качестве произвольной замкнутой поверхности S выберем цилиндр длиной l , ось которого перпендикулярна плоскости, а основания равноудалены от нее (рис. 1.10). Общий поток электрического поля Ф Фосн Фбок . Поток через

28

боковую поверхность равен нулю. Поток через каждое из оснований равен ESосн , поэтому Фосн 2ESосн . По теореме Гаусса получим

Сумму зарядов, находящихся внутри цилиндра S, найдем через поверхностную плотность заряда :

qi Sосн . Тогда 2ESосн σ Sосн 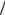ε0 , откуда

i

Из полученной формулы видно, что напряженность поля равномерно заряженной плоскости не зависит от расстояния до заряженной плоскости, т.е. в любой точке пространства (в одной полуплоскости) одинакова и по модулю, и по направлению. Такое поле называется однородным. Силовые линии однородного поля параллельны, их густота не меняется.

Найдем разность потенциалов между двумя точками однородного поля (принадлежащим эквипотенциальным плоскостям 1 и 2 , лежащим в одной полуплоскости от-

носительно заряженной плоскости (см. рис. 1.10)). Направим ось x вертикально вверх, тогда проекция вектора напряженности на эту ось равна модулю вектора напряженности Ex E . Воспользуемся уравнением (1.9):

29

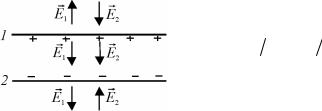
руя, получаем: 1 2 Е х2 х1 . Итак, потенциал одно-

родного поля линейно зависит от координаты.

Разность потенциалов между двумя точками электрического поля есть напряжение между этими точками (U ). Обозначим расстояние между эквипотенциальными плоскостями х1 х2 d . Тогда можно записать, что в однород-

ном электрическом поле

Еще раз подчеркнем, что при использовании формулы (1.21) нужно помнить, что величина d не расстояние между точками 1 и 2, а расстояние между эквипотенциальными плоскостями, которым эти точки принадлежат.

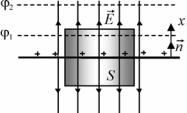
Пример 1.4. Рассчитать напряженность электрического поля двух параллельных плоскостей, однородно заряженных с поверхностными плотностями зарядов и .

Решение. Воспользуемся результатом примера 1.3 и принципом суперпозиции. Согласно этому принципу, результирующее электрическое поле в любой точке про-

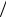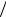странства Е Е1 Е2 , где Е1 и Е2 – напряженности электрических полей первой и второй плоскости. В пространстве между плоскостями вектора Е1 и Е2 направлены в одну сторону, поэтому модуль напряженности результирующего поля Е σ 2ε0 σ 2ε0 σε0 . Во внешнем пространст-

30