
Физика. Ч. II Основы электромагнетизма учебное пособие
.pdfния некоторой физической величины x называются гармоническими, если она изменяется со временем по закону косинуса или синуса, т.е.
x Acos t 0 , |
(4.1) |
где A амплитуда колебаний (максимальное отклонение смещения x от положения равновесия); 2 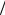 T 2
T 2
циклическая частота колебаний (T период, частота колебаний); t 0 фаза, 0 начальная фаза ко-
лебаний. Первая и вторая производные величины x по времени:
x A sin t 0 , x A 2cos t 0 .
Из последнего уравнения с учетом (4.1) следует |
x 2 x |
или: |
|
x 2 x 0 . |
(4.2) |
Соотношение (4.2) представляет собой дифференциальное уравнение гармонических колебаний.
Мы показали, что если какая-либо физическая величина совершает гармонические колебания, т.е. изменяется по закону (4.1), то для нее справедливо дифференциальное уравнение (4.2). В курсе дифференциальных уравнений доказывается и обратное утверждение: если для какой-либо физической величины удалось (используя законы физики) написать дифференциальное уравнение (4.2), то единственным его решением будет уравнение (4.1), т.е. величина x совершает гармонические колебания. При этом амплитуда A и начальная фаза 0 определяются начальными усло-
виями, т.е. значениями величины x и ее первой производной x в начальный момент времени t 0 . Другими словами, определяются тем, каким образом экспериментатор запустит маятник.
221

Теперь рассмотрим задачу о колебаниях в LC-кон- туре. В контуре действует единственная электродвижущая сила – ЭДС самоиндукции S . Согласно закону Ома для
неоднородного участка цепи, начало которого – положительная обкладка конденсатора, а конец – отрицательная (рис. 4.1, б), можно записать: ( 1 2 ) S IR , где
( 1 2 ) UC разность потенциалов или напряжение ме-
жду обкладками конденсатора. Т.к. сопротивление контура R 0 , то:
UC S 0 Cq L ddIt 0 .
По определению сила тока – это заряд, протекающий через сечение проводника за единицу времени, т.е. производная заряда по времени (см. формулу (2.1)). Если q это заряд
положительной обкладки, то величина тока в контуре I dq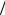 dt q . Знак минус учитывает тот факт, что после
dt q . Знак минус учитывает тот факт, что после
замыкания ключа заряд положительной обкладки убывает ( dq 0 ). Тогда производная тока по времени есть вторая
производная заряда по времени: dI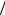 dt I q . В результате получим:
dt I q . В результате получим:
q |
L dI |
0 |
|
q |
Lq 0. |
(4.3) |
|
C |
C |
||||||
dt |
|
|
|
|
Отметим, что в электротехнике величина ЭДС самоиндукции, взятая с обратным знаком, рассматривается как на-
пряжение на катушке (индуктивности): UL S LI Lq . Поэтому уравнение (4.3) можно записать в виде
UC UL 0. |
(4.4) |
Уравнение (4.4) представляет собой, по сути, обобщение второго правила Кирхгофа, сформулированного нами ранее
222

(см. подраздел 2.7) для замкнутых контуров с постоянными токами: сумма падений напряжений в замкнутом контуре равна алгебраической сумме внешних ЭДС, действующих в контуре. Внешние ЭДС в LC-контуре не действуют (ЭДС самоиндукции – это напряжение на индуктивности, внутренняя ЭДС).
Разделив обе части уравнения (4.3) на величину L , получим:
q |
1 |
q 0 . |
(4.5) |
|
LC |
||||
|
|
|
Уравнение (4.5) по форме совпадает с уравнением (4.2), т.е. является дифференциальным уравнением гармонических колебаний. Роль физической величины x играет заряд на обкладках конденсатора q . Можно сделать два вывода:
во-первых, заряд на обкладках конденсатора изменяет по гармоническому закону
q q0cos t 0 ; |
(4.6) |
во-вторых, квадрат циклической частоты колебаний (коэффициент при q в уравнении (4.5)): 2 1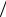 LC , откуда
LC , откуда
|
|
1 |
. |
(4.7) |
|
|
|||
|
|
LC |
|
|
Период колебаний связан |
с циклической |
частотой |
||
Т 2 , тогда |
|
|
|
|
Т 2 |
LC . |
(4.8) |
||
Формула (4.8) для периода колебаний заряда в LC-контуре называется формулой Томсона.
По гармоническому закону будут изменяться и другие физические величины, характеризующие процесс коле-
223
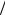
баний в LC-контуре. Зависимость напряжения на обкладках конденсатора от времени:
UC |
q |
|
q0 |
cos t 0 U0cos t 0 , (4.9) |
|
C |
C |
||||
|
|
|
где U0 максимальное напряжение или амплитуда напря-
жения на конденсаторе.
Зависимость от времени силы тока найдется дифференцированием заряда по времени:
I q q0 sin t 0 I0sin t 0 , (4.10)
где I0 q0 максимальный ток в контуре или амплитуда тока. Воспользовавшись известной формулой тригонометрии sin cos 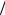 2 (формулой приведения), колебания тока можно записать через функцию косинус:
2 (формулой приведения), колебания тока можно записать через функцию косинус:
I I0cos t 0 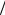 2 .
2 .
Сравнение последнего выражения с уравнением (4.6) показывает, что колебание тока отличается от колебания заряда (и напряжения) конденсатора по фазе на / 2 . Это означает, что в тот момент, когда заряд конденсатора и напряжение на нем максимальны, т.е. cos 1 (напомним,
что t 0 фаза), |
ток в контуре равен нулю |
(если |
cos 1 , то sin cos |
2 0 ). И наоборот, |
когда |
ток максимален, заряд и напряжение на конденсаторе равны нулю. На рис. 4.2 показаны состояния LC-контура в моменты времени t 0, T / 4, T / 2, 3T / 4, T , где T период колебаний. Предполагается, что в начальный момент времени ( t 0 ) заряд конденсатора максимален.
Гармонические колебания будут совершать также величины ЭДС самоиндукции, энергий электрического поля конденсатора и магнитного поля катушки. Предлага-
224
Рис. 4.2. Состояния LC-контура в различные моменты времени
ем читателям вывести соответствующие выражения самостоятельно.
Пример. 4.1. Максимальное значение напряжения на обкладках конденсатора LC-контура U0 10 В. Определить
значение силы тока W0 CU202 в контуре в тот момент, ко-
гда напряжение на конденсаторе станет равным U1 5 В, если C 50 нФ, L 0,01 Гн.
Решение. Задачу можно решить, используя уравнения колебаний напряжения и тока (4.9) и (4.10). Однако проще воспользоваться законом сохранения энергии.
При колебаниях в LC-контуре энергия электрического поля конденсатора переходит в энергию магнитного поля катушки, и наоборот. Суммарная энергия электрического поля конденсатора и магнитного поля катушки в любой мо-
мент времени остается неизменной: CU 2 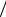 2 LI 2
2 LI 2  2 const .
2 const .
В начальный момент времени напряжение на конденсаторе и его заряд максимальны. При этом сила тока в цепи равна нулю (см. рис. 4.2) и полный запас энергии контура состоит из энергии электрического поля конденсатора:
225

W0 CU02 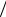 2 . В промежутке времени между t 0 и t T / 4
2 . В промежутке времени между t 0 и t T / 4
по цепи идет ток, но конденсатор еще полностью не разрядился. Поэтому энергия контура в конечный момент вре-
мени W1 CU12 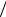 2 LI12
2 LI12 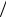 2 . Таким образом,
2 . Таким образом,
|
W W |
|
|
|
CU |
2 |
|
CU |
2 |
LI |
2 |
|
|
|||
|
|
|
|
0 |
|
|
1 |
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 |
1 |
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
I |
|
C U0 |
2 |
U12 |
|
|
50 10 9 100 25 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
L |
|
|
|
|
|
|
0,01 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
19,4 10 3 (А) 19,4 (мА).
4.2.Колебательный контур с затуханием
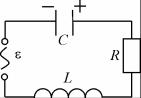
Колебательный контур без сопротивления это идеальная модель. На самом деле LC-контур всегда обладает некоторым сопротивлением R, хотя бы за счет подводящих проводов. Рассмотрим LC-контур
ссопротивлением R (рис. 4.3). Такой контур называется контуром
сзатуханием или LCR-контуром. При замыкании обкладок заряженного конденсатора в контуре
начинаются колебания. Однако теперь при протекании электриче-
ского тока за счет сопротивления R контур нагревается. Энергия электрического поля, первоначально запасенная в конденсаторе, постепенно переходит во внутреннюю энергию провода, амплитуды колебаний всех электрических величин уменьшаются вплоть до полного прекращения колебаний.
Дифференциальное уравнение затухающих колебаний некоторой физической величины x имеет вид:
x 2 x 2 x 0. |
(4.10) |
0 |
|
226
Оно отличается от дифференциального уравнения гармонических колебаний (4.2) слагаемым ( 2 x ), учитываю-
щим силы сопротивления, действующие на маятник. Коэф-
фициент называется коэффициентом затухания. Если величина x смещение, ее производная x скорость, тогда слагаемое (2 x) отражает тот факт, что сила сопро-
тивления пропорциональна скорости.
В случае, когда затухание не слишком велико (выполняется условие 0 ), решение дифференциального уравнения (4.10) имеет вид:
x A0e t cos t 0 , |
(4.11) |
где A0e t A t амплитуда колебаний, уменьшающаяся со временем по экспоненциальному закону; A0 начальная
амплитуда колебаний; |
2 |
2 |
циклическая частота |
|
0 |
|
|
колебаний; 0 собственная циклическая частота колеба-
ний (частота, с которой колебался бы маятник, если бы сил сопротивления не было). Присутствие сил сопротивления уменьшает циклическую частоту колебаний и, соответственно, увеличивает период колебаний:
T |
2 |
|
2 |
. |
|
|
|||
|
|
02 2 |
||
Вернемся к электромагнитным колебаниям в LCR- контуре. Поскольку внешние ЭДС в цепи не действуют, сумма падений напряжений на отдельных элементах контура равна нулю:
UL UR UC 0 LI IR Cq 0 .
Учитывая, что I q , получим:
Lq Rq |
q |
0 |
q |
R |
q |
|
q |
0 . |
(4.12) |
C |
|
LC |
|||||||
|
|
|
L |
|
|
|
|||
227
Уравнение (4.12) по форме совпадает с дифференциальным уравнением (4.10). Отсюда можно сделать два основных вывода.
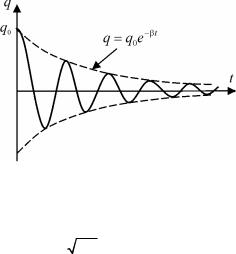
1. Процесс в LCR-контуре представляет собой затухающие колебания, зависимость заряда конденсатора от времени подобна (4.11):
|
|
q q0e t cos t 0 . |
(4.13) |
|||
График |
функции |
|
|
|
||
|
|
|
||||
(4.13) |
изображен |
|
|
|
||
на рис. 4.4. сплош- |
|
|
|
|||
ной линией. От- |
|
|
|
|||
дельно пунктирной |
|
|
|
|||
линией |
показана |
|
|
|
||
зависимость |
ам- |
|
|
|
||
плитуды |
колеба- |
|
|
|
||
ний заряда от вре- |
|
|
|
|||
мени A t q0e t . |
|
|
|
|||
Рис. 4.4. Зависимость заряда конденсато- |
||||||
2) Сравнение |
||||||
ра от времени при затухающих колеба- |
||||||
коэффициентов |
|
ниях в LCR-контуре |
|
|
||
уравнений (4.10) и(4.12) показывает, что собственная циклическая частота колебаний 0 1 LC , а коэффициент затухания R
LC , а коэффициент затухания R 2L .
2L .
Сформулируем несколько определений параметров затухающих колебаний.
Время , в течение которого амплитуда колебаний уменьшается в e 2,72 раз, называется временем затухания
или временем релаксации.
Отметим, что уменьшение амплитуды почти в 3 раза существенно, однако не означает полного прекращения колебаний.
228
Время затухания есть величина, обратная коэффициенту затухания :
1 . |
(4.14) |
Докажем утверждение (4.14). Амплитуда колебаний в не-
который момент |
времени |
t : A q e t . Через время |
|
, |
|||||
|
|
|
|
|
1 |
0 |
|
|
|
т.е. в |
момент |
времени |
t , |
амплитуда колебаний |
|||||
A q e t . По определению величины |
|
|
|||||||
2 |
0 |
|
|
|
|
|
|
|
|
A / A e |
q e t |
e |
e t e 1 |
1 |
. |
||||
0 |
|
|
|||||||
q0e t |
|
||||||||
1 |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
Из формулы (4.14) следует, что 1/ . Таким обра-
зом, коэффициент затухания – это величина, обратная времени затухания, т.е. времени, за которое амплитуда уменьшается в e раз.
Декрементом затухания называется величина,
равная отношению амплитуд следующих друг за другом колебаний:
AN |
AN 1 , |
|
(4.15) |
где AN амплитуда N-го колебания; |
AN 1 |
амплитуда |
|
N 1 -го колебания. |
|
|
|
Декремент затухания связан с коэффициентом затухания и периодом колебаний T :
e T . |
(4.16) |
Докажем формулу (4.16). Пусть N-е колебание происходит
в некоторый момент времени t , тогда A |
q |
e t . По- |
N |
0 |
|
скольку (N + 1)-е и N-е колебания разделены временным отрезком, равным периоду колебаний T , то AN 1 q0e t T .
q e t
Тогда q0e0 t T e T .
229
Логарифмическим декрементом затухания называет-
ся величина ln . Из формулы (4.16) следует:
ln e T T . |
(4.17) |
Пример 4.2. Определить число колебаний маятника за время затухания, если известен логарифмический декремент затухания .
Решение. Число колебаний можно найти, разделив полное время колебаний (в данном случае время затухания ) на время одного колебания, т.е. на период T : N 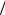 T . Далее, используя формулу (4.14), получим ответ:
T . Далее, используя формулу (4.14), получим ответ:
N 1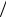 T 1
T 1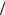 . Следствие: 1
. Следствие: 1 N , т.е. логарифмиче-
N , т.е. логарифмиче-
ский декремент затухания есть величина, обратная числу колебаний за время затухания.
4.3. Вынужденные колебания в LCR-контуре
Для того чтобы поддерживать колебания в LCR- контуре, необходимо пополнять запасы энергии, непрерывно рассеиваемой в виде тепла на сопротивлении R . Это можно с помощью воздействия на контур внешней периодической электродвижущей силы (рис. 4.5).
При этом в контуре возникнут вынужденные колебания. Будем рассматривать синусоидальную ЭДС, т.е. ЭДС, зависящую от времени по закону синуса (или косинуса):
0sin t ,
где циклическая частота колебаний ЭДС.
230
