
Физика. Ч. II Основы электромагнетизма учебное пособие
.pdfПример 1.5. Найти напряженность и потенциал электрического поля равномерно заряженной сферы. Суммарный заряд сферы равен Q , а радиус сферы – R .
Решение. В силу симметрии распределения заряда силовые линии должны быть направлены вдоль радиусов сферы.
Рассмотрим область внутри сферы. В качестве произвольной поверхности S выберем сферу радиуса r R , центр которой совпадает с центром заряженной сферы. Тогда поток электрического поля через сферу S: Ф ESсф .
Сумма зарядов внутри сферы S радиуса r равна нулю, поскольку все заряды располагаются на поверхности сферы радиуса R r . Тогда по теореме Гаусса ЕSсф 0 . Посколь-
ку Sсф 0 , то E 0 . Таким образом, внутри равномерно
заряженной сферы поля нет.
Рассмотрим область вне сферы. В качестве произвольной поверхности S выберем сферу радиуса r R , центр которой совпадает с центром заряженной сферы. Поток электрического поля через сферу S : Ф ESсф . Сумма
зарядов внутри сферы равна полному заряду Q заряженной сферы радиуса R . Тогда по теореме Гаусса ESсф Q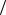 0 . Учитывая, что Sсф 4 r2 , получим:
0 . Учитывая, что Sсф 4 r2 , получим:
E |
Q |
k |
Q |
. |
4 0r2 |
|
|||
|
|
r2 |
||
Рассчитаем потенциал электрического поля. Удобнее начать с внешней области r R , поскольку мы знаем, что на бесконечном расстоянии от центра сферы потенциал принимается равным нулю. Используя уравнение (1.11, а)
31

получаем дифференциальное уравнение с разделяющимися переменными:
|
k |
Q |
d d k |
Q |
dr |
|
|
|||
|
|
|
|
|
||||||
|
|
r2 |
dr |
|
r2 |
|
|
|
||
|
|
|
|
dr |
|
|
Q |
|
|
|
|
d kQ r2 |
k r |
C1 . |
|
|
|||||
|
Константа С1 0 , поскольку 0 |
при |
r . Та- |
|||||||
ким |
образом, |
во |
внешнем |
пространстве, |
где r R, |
|||||
k Q r . |
|
|
|
|
|
|
|
|
|
|
|
Точки на поверхности заряженной сферы ( r R ) бу- |
|||||||||
дут иметь потенциал k Q R . |
|
|
|
|||||||
|
Рассмотрим область r R . В этой области E 0 , по- |
|||||||||
этому |
из уравнения |
(1.11, а) |
получаем: |
0 d dr |
|
|||||
C2 . В силу непрерывности функции (r) константа C2 должна быть равна значению потенциала на поверхности заряженной сферы: С2 k Q R . Таким образом, потенциал во всех точках внутри сферы k Q
R . Таким образом, потенциал во всех точках внутри сферы k Q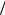 R .
R .
Итак, мы получили, что напряженность и потенциал электрического поля, создаваемого равномерно заряженной сферой, вне сферы равны напряженности и потенциалу поля, создаваемого точечным зарядом той же величины Q ,
что и заряд сферы, помещенным в центр сферы. Во внутреннем пространстве поле отсутствует, а потенциал во всех точках одинаков. Электрическое поле (силовые линии и эквипотенциальные поверхности) заряженной сферы изображены на рис. 1.12. Предполагается, что сфера заряжена положительно. Вне сферы силовые линии распределены в пространстве точно так же, как и силовые линии точечного заряда.
32

На рис. 1.13 изображены графики зависимости Е(r)
и (r) . Функция (r) непрерывна, а функция Е(r) скачко-
образно меняется при переходе через границу заряженной сферы. Величина скачка равна
k Q R2 . Действительно, вблизи
R2 . Действительно, вблизи
заряженной сферы ( r R ) напряженность поля во внешнем пространстве k Q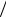 R2 , а внутри равна нулю.
R2 , а внутри равна нулю.
Рис. 1.12. Схема к расчету электрического поля равномерно заряженной сферы
Рис. 1.13. Распределение напряженности и потенциала около равномерно заряженной сферы
Величину скачка можно выразить через поверхностную плотность заряда на сфере:
E k |
Q |
|
Q |
|
|
. |
R2 |
4 0 R2 |
|
||||
|
|
|
0 |
|||
Заметим, что это общее свойство электростатического поля: на заряженной поверхности проекция напряженности на направление нормали всегда испытывает скачок E 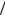 0 , независимо от формы поверхности. Реко-
0 , независимо от формы поверхности. Реко-
мендуем проверить этот принцип для поля равномерно заряженной плоскости и поля двух параллельных заряженных плоскостей (примеры 1.3, 1.4).
33

С точки зрения математики непрерывность потен-
циала |
в точках |
|
заряженной поверхности означает, |
что lim (r) lim |
(r) . С точки зрения физики непрерыв- |
||
r R 0 |
r R 0 |
|
|
ность функции (r) |
можно объяснить следующим обра- |
||
зом. Если бы потенциал на границе некоторой области имел скачок (разрыв), то при бесконечно малом перемещении некоторого заряда q из точки 1, лежащей с одной сто-
роны границы, в точку 2, лежащую на другой ее стороне,
совершалась бы конечная работа А q( 1 2 ) , где |
1 |
и 2 потенциалы точек 1 и 2 соответственно, а величина ( 1 2 ) равна величине скачка потенциала на границе об-
ласти. Конечная работа, совершенная на бесконечно малом перемещении, означает, что на границе раздела бы действовали бесконечно большие силы, что невозможно.
Напряженность электрического поля, в отличие от потенциала, на границе области может меняться очень резко (скачкообразно).
Пример 1.6. Две концентрические сферы радиусов R1 и R2 ( R1 R2 ) равномерно заряжены равными по модулю, но противоположными по знаку зарядами Q и Q (сфе-
рический конденсатор). Определить |
напряженность |
и потенциал электрического поля во всем |
пространстве. |
Решение. Решение этой задачи можно было бы также начать с применения теоремы Гаусса. Однако, используя результаты предыдущего примера и принцип суперпозиции (1.13, 1.14), ответ можно получить быстрее.
Во внешних точках пространства ( r R2 ) электрическое поле создается зарядами обеих сфер. Величина напряженности поля первой сферы E1 k Q
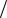 r2 и направлена
r2 и направлена
34

от сфер вдоль радиусов. Величина напряженности поля
второй сферы такая же E2 |
k |
|
Q |
|
r2 , но направлена про- |
|
|
тивоположно. Следовательно, согласно принципу суперпозиции, во всех внешних точках пространства электрическое
поле будет отсутствовать: Е Е1 Е2 0 .
Рассмотрим точки пространства между сферами ( R1 r R2 ). Эти точки являются внутренними для отрица-
тельно заряженной сферы, поэтому в этой области Е2 0 (см. пример 1.5). Для положительно заряженной сферы эти
точки являются внешними, поэтому E k |
|
Q |
|
r2 |
. Таким |
|||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
образом, |
величина |
напряженности |
поля в |
|
этой |
области |
||||||||||||||
Е E k |
|
Q |
|
r2 |
. Здесь поле создают только заряды мень- |
|||||||||||||||
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шей сферы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Наконец, |
во |
|
внутренних |
точках |
|
пространства |
||||||||||||||
( r R1 ) |
Е1 0 |
и Е2 0 , поэтому |
электрического поля |
|||||||||||||||||
в этих точках нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Можно применить принцип суперпозиции и для по- |
||||||||||||||||||||
тенциалов. Получаются следующие результаты: |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
r R2 : 0 ; |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
R r R : k Q k |
Q |
; |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
r |
|
R2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
r R : k |
Q |
k |
Q |
|
const. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
R1 |
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рекомендуем самостоятельно получить эти результаты, а также схематически изобразить электрическое поле и построить графики Е(r) и (r) .
35
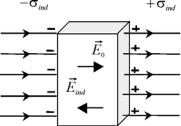
тельно, будет равна нулю и сила, действующая на электроны внутри металла. В результате под действием внешнего электрического поля на поверхности пластины появятся заряды с поверхностной плотностью ind и ind . Эти за-
ряды называются индуцированными. Электрическое поле индуцированных зарядов и компенсирует внешнее электрическое поле.
Пример 1.7. Тонкую металлическую пластину помещают в однородное электрическое поле напряженностью Е0 100 кВ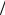 м перпендикулярно силовым линиям. Опре-
м перпендикулярно силовым линиям. Опре-
делить поверхностную плотность индуцированных зарядов на гранях пластины.
Решение: В равновесии напряженность электрического поля внутри металла равна нулю. С другой стороны, она
складывается из напряженности внешнего поля Е0 и напряженности поля, созданного индуцированными зарядами Еind . Т.к. пластина достаточно тонкая, то можно допус-
тить, что электрическое поле индуцированных зарядов однородно, и рассчитать его так же, как поле двух равномерно заряженных плоскостей (см. пример 1.4): Еind ind  0 .
0 .
Таким образом:
0 Е |
Е |
|
ind |
|
Е 8,85 10 12 |
105 |
|
0 |
ind |
|
0 |
0 |
|
|
8,85 10 7 (Кл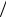 м2 ) .
м2 ) .
Поверхностную плотность индукционных зарядов можно представить в виде еn , где е модуль заряда электрона, а n число электронов, приходящееся на единицу поверхности:
n |
|
|
8,85 10 7 |
12 |
шт./м |
2 |
. |
|
e |
1,6 10 |
19 |
5,5 10 |
|
||||
|
|
|
|
|
|
|
||
37

Для компенсации внешнего поля достаточно ничтожной доли от общего числа электронов 1023 шт./см3
в металле.
Мы рассмотрели пример с металлической пластиной. Естественно, что в равновесии электрическое поле внутри металла будет равно нулю в образцах любой формы. Индуцированные заряды всегда текут в такие участки поверхности проводника, чтобы поле внутри него обратилось в нуль.
Пример 1.8. Доказать, что все точки металла имеют один и тот же потенциал, т.е. металлы – эквипотенциальны.
Решение. В равновесии поле внутри металла отсутствует: Е 0 . Воспользуемся уравнением (1.10):
d |
0, |
|
dx |
|
|
0 grad d |
0, |
const . |
dy |
|
|
d |
0. |
|
dz |
|
|
Поскольку силовые линии перпендикулярны эквипотенциальным поверхностям, электрическое поле вблизи
проводника должно |
быть нормально к его |
поверхности. |
|||
|
|
(Это понятно, т.к. если бы поле |
|||
|
|
имело |
касательную |
составляю- |
|
|
|
щую, то электроны задвигались бы |
|||
|
|
вдоль |
поверхности |
проводника. |
|
|
|
В качестве примера |
на рис. 1.15 |
||
|
|
показано электрическое поле то- |
|||
Рис. 1.15. Электриче- |
|
чечного заряда вблизи поверхно- |
|||
|
сти Земли (Земля – проводник). |
||||
ское поле точечного |
|
Напомним, что тело является |
|||
заряда вблизи поверхно- |
|||||
заряженным, если количество отри- |
|||||
сти Земли |
|
||||
цательных зарядов частиц, из кото-
38
рых оно состоит, не совпадает с количеством положительных. Если же количество отрицательных и положительных зарядов частиц совпадают, то отрицательный суммарный заряд тела компенсируется положительным суммарным зарядом и тело является нейтральным.
Пример 1.9. Доказать, что внутри заряженных металлов (проводников) не может быть свободных нескомпенсированных зарядов. Весь заряд металла располагается на его поверхности.
Решение: Используем теорему Гаусса. Выберем внутри металла произвольную замкнутую поверхность, тогда поток электрического поля через эту поверхность Ф = 0, поскольку в равновесии внутри металла поле отсутствует,
т.е. Е 0. По теореме Гаусса получаем: |
0 qi |
0 , отку- |
|
i |
|
да следует доказываемое утверждение: qi 0 , т.е. об-
i
ласть, ограниченная произвольно выбранной поверхностью внутри металла, оказывается нейтральной. Весь нескомпенсированный заряд металла может располагаться только на его поверхности.
Результат, полученный в примере 1.9, можно объяснить следующим образом. Нескомпенсированные электрические заряды должны располагаться на поверхности проводника потому, что между ними действуют кулоновские силы отталкивания. Эти силы заставляют одноименные заряды разойтись на как можно большее расстояние друг от друга, т.е. расположиться на поверхности проводника. Поверхностная плотность электричества будет максимальна на наиболее удаленных выступающих частях проводника, например на остриях. Поверхностная плотность зарядов на остриях может быть настолько большой, что возникает
39
электрический пробой воздуха. Вблизи острия воздух ионизируется, становится проводником и «снимает» заряды с острия. На этом основано действие молниеотвода. Заряженные тучи нейтрализуются, «снимая» заряды противоположных знаков прежде всего с наиболее выступающих, острых предметов на поверхности Земли.
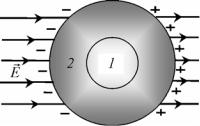
Теперь поместим во внешнее электрическое поле пустотелый проводник, например, металлический шар с полостью (рис. 1.16). Мысленно заполним объем полости 1 металлом. Тогда поле повсюду внутри шара будет равно нулю. При этом на поверхности шара возникнут индуцированные заряды, поле которых компенсирует внешнее поле. Объем 1 в целом электрически нейтрален (см. пример 1.9). Если теперь «вырезать» этот
объем, это никак не скажется на равновесии индуцированных зарядов на поверхности проводника. Следовательно, не изменится и электрическое поле индуцированных зарядов. Оно по-прежнему будет компенсировать внешнее электрическое поле, теперь уже в полости. Таким образом, если полость целиком окружить проводником, то внутри полости электрическое поле будет отсутствовать, как и в толще проводника. На этом основан принцип электростатической защиты различного оборудования, которое помещается внутрь металлической полости.
40
