
- •Ноу «Институт специальной педагогики и психологии» а. П. Бизюк
- •Санкт-Петербург 2009
- •1.1. Определение
- •1.2. Программа подготовки
- •1.2.1. Выбор темы
- •1.2.2. Планирование
- •1.3. Структура дипломной работы
- •1.3.1. Оглавление
- •1.3.2. Введение
- •1.3.2,1. Актуальность
- •1.3.2.3. Объект исследования
- •1.3.2.5. Предмет исследования
- •1.3.2.7. Задачи исследования
- •1.3.2.8. Описание методик
- •1.3.2.9. Практическая значимость
- •1.3.2.10. Научная новизна
- •1.3.3.2. Использование Интернета
- •1.3.3.5. Оптимизация обзора литературы
- •1.3.4» Экспериментальный раздел 1.3.4.1. Структура раздела
- •Пример приведения результатов факторного анализа
- •1 Г— I t |[ ( •
- •1.3.5. Заключение и выводы
- •1.3.6. Практические рекомендации
- •2. Оформление дипломной работы
- •2.1. Общие требования
- •2.2. Заголовки
- •1.1. Хххххх ххххххх хххх ххххххх [Параграф]
- •2.4. Нумерация
- •2.5. Титульный лист
- •2.6. Оглавление (содержание)
- •2.7. Таблицы
- •Продолжение табл. О
- •2.8. Другие иллюстрации
- •2.9. Приложение
- •2.10. Внутритекстовые ссылки
- •2.11. Список литературы
- •3. Процедура зашиты
- •4. Этикет
- •5. Основныеориентиры
- •Кафедра специальной психологии, кафедра психологии развития личности, кафедра основ физиологии
- •Институт специальной педагогики и психологии Кафедра Ххххжххххххх хххххххххх
- •Дипломная работа
Таблица
1
Переменные
Фактор
1
Фактор
2
Фактор
3
А
-0,309
0,891
-0,326
6
-0,661
-0,452
0,355
С
0,813
-0,480
0,037
D
0,077
0,348
0,924
Е
0,774
0,081
-0,413
F
-0,733
-0,378
-0,480
Объяснимая
2,338
1,502
1,489
дисперсия
Пример приведения результатов факторного анализа
гументация содержания, фактически угадываемого в том или ином факторе - самая сложная и противоречивая задача. Например, если с большими положительными весами в один из выделившихся факторов вошли такие переменные, как высокий рост, грубый голос, большая мышечная масса, склонность к риску, широкие плечи, агрессивное поведение, то вероятнее всего подобная комбинация антропологом будет трактоваться как фактор мужского пола, эндокринолог увидит влияние какого-то гормона, а психолог попытается найти некие аналоги в типологии личности. Особо широко в психологии приемы факторного анализа представлены при попытках произвести упорядочение (объединение в шкалы) многочисленных пунктов в объемных личностных опросниках.
Большинство программ факторного анализа построено таким образом, что первый выделившийся фактор обладает самым большим влиянием на разброс показателей в группе (объяснимая дисперсия), а значение остальных факторов последовательно убывает.
Существует несколько основных форм факторного анализа, дающих в итоге различные результаты. Выбор необходимого варианта диктуется конкретными задачами дипломного исследования.
❖ Кластерный анализ
Если вам необходимо разбить множество ваших переменных (объектов) на заданное или неизвестное число классов, то целесообразно использовать кластерный анализ(cluster - гроздь, пучок, скопление, группа элементов, характеризуемых каким-либо общим свойством). Это не слишком часто используемая в дипломных работах форма математической обработки эмпирических материалов, представляющая интерес в тех случаях, когда переменных достаточно мно-
90
70
Рис. 3. Пример одного из вариантов графического представления результатов кластерного анализа шести переменных.
го и хочется наглядно увидеть их упорядоченность - в каких иерархических отношениях находятся переменные более высокого уровня обобщенности к более конкретным, частным (рис. 3).
Весьма любопытные результаты, тяготеющие к сфере психолингвистики, с помощью кластерного анализа можно получить при применении его к пунктам психологических тестов, вопросам опросников и анкет.
Существует точка зрения, что в отличие от многих других статистических процедур, методы кластерного анализа используются в большинстве случаев тогда, когда еще не имеется каких-либо гипотез относительно классов, т. е. когда вы все еще находитесь в описательной стадии исследования.
Пользоваться результатами кластерного анализа нужно осторожно, поскольку он может навязывать экспериментатору гипотезу об отношениях переменных, построенную на внешних, формальных критериях и не учитывать их качественную специфику. Для того, чтобы избежать подобной ошибки, предпочтительно применять несколько разных алгоритмов расчета (их много, техники группировки отличаются) и выбрать из результатов тот, который лучше всего объясняется с позиции здравого смысла. Следует понимать, что кластерный анализ определяет «наиболее возможно значимое решение».
❖ Дискримииантный анализ
Еще один из методов статистической обработки, который может оказаться полезным в дипломной работе, называется дискриминант- ним анализом.Суть его состоит в том, что он позволяет делить обладающие какими-то признаками объекты или состояния, относя их к како- му-либо классу или оценивать близость конкретного состояния к одному из классов. Сама исследовательская процедура дискриминан- тного анализа состоит из нескольких шагов:
определяются группы, которые в дальнейшем нужно различать (например, больных истерическим неврозом от больных неврозом навязчивых состояний) - это так называемая обучающая выборка;
эти группы, каждый член которых уже имеет точный (верифицированный) диагноз, исследуются по максимальному числу признаков (текущая симптоматика, личностная предрасположенность, специфика семейного воспитания, характер психотравмирующих ситуаций и т. п.);
по каждому из исследованных признаков вся обучающая выборка (и тех и других больных) дискриминируется и отслеживается - насколько точно данный признак разделил группу по диагнозам по сравнению с фактическим положением дел;
из всех просмотренных признаков отбираются наиболее информативные (те, которые наиболее точно делят обучающую выборку) и в дальнейшем они начинают использоваться для улучшения точности диагноза у тех, кому он еще не поставлен;
44
- попутно, при необходимости, можно отследить, насколько близко или далеко находится каждый из обследованных индивидов к тому или другому состоянию.
В итоге дискриминантного анализа для каждой переменной вы получите стандартизованный коэффициент (Т - лямбда Уилк- са), интерпретируемый следующим образом: чем он больше, тем меньше вклад соответствующей переменной в различение совокупностей.
Другими словами, основная идея дискриминантного анализа заключается в том, чтобы определить, отличаются ли совокупности по среднему какой-либо переменной (или их комбинации), и затем использовать эту переменную, чтобы предсказать для новых членов их принадлежность к той или иной группе (это задача прогноза). Более простой пример: показатель роста может служить дискриминирующим признаком для отнесения неизвестного нам человека к мужскому или женскому полу, поскольку уже точно известно, что средний рост мужчины выше среднего роста женщины.
Один подобный признак, как можно догадаться из представленного примера, не гарантирует надежности прогноза, но совокупность характеристик может сделать его достаточно уверенным.
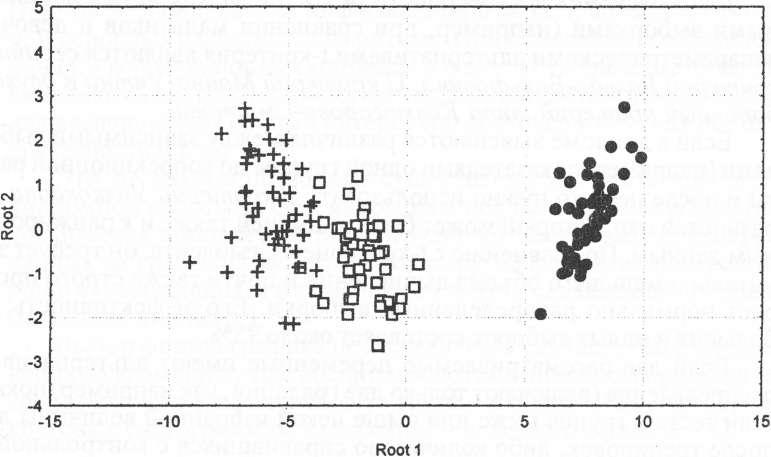
Ниже приводится иллюстрация графического представления дискриминантного анализа (рис. 4).
Root
1 vs. Root2
Рис.
4. Графический пример разделения
носителей признака на три группы,
полученный в результате дискриминантного
анализа.
❖ Непараметрические методы
Еще раз хотелось бы подчеркнуть, что все рассмотренные процедуры статистического анализа могут быть корректно использованы только в том случае, если ваши экспериментальные данные подчиняются т. н. нормальному закону распределения или хотя бы приближаются к нему. Это значит, что в имеющемся у вас распределении крайние значения признака - и наименьшие и наибольшие - появляются редко, а чем ближе значение признака к средней арифметической, тем чаще оно встречается (см. рис. 1).
Если такого соответствия нет, что, как правило, объясняется либо малыми размерами выборки (менее 20—30), либо измерениями в порядковых шкалах (типа «высокий», «средний», «низкий»), либо тем, что переменные объективно распределены «ненормально», то для обработки эмпирических материалов диплома нужно использовать так называемые непараметрические критерии, хотя они и имеют меньшую мощность и обладают меньшей гибкостью (для их расчета не рассматриваются и не учитываются значения среднего и стандартного отклонения). Но у них есть и ряд преимуществ. Они малочувствительны к неточным измерениям и эти методы могут применяться для обработки данных, имеющих полуколичественную природу (ранги, баллы и т. д.). Кроме того, с их помощью можно получить ответы на такие вопросы, которые неразрешимы с использованием методов, основанных на нормальном распределении. Следовательно, они иногда оказываются уместны и для обработки нормально распределенных результатов исследования.
Не вдаваясь в подробности, укажем лишь на названия непараметрических процедур, позволяющих получить показатели, аналогичные нормально распределенным.
Для выяснения достоверности различий между двумя независимыми выборками (например, при сравнении мальчиков и девочек) непараметрическими альтернативами t-критерия являются серийный критерий В альд а-Вольфовичa, U критерий Манна-Уитнии двухвы- бор очный критерий типа Колмогорова-Смирнова.
Если в дипломе выясняются различия между зависимыми выборками (например, показателями одной группы до коррекционной работы и после нее), то нужно использовать Т-критерий Уилкоксонадля разностей пар, который может быть применен также и к ранжированным данным. По сравнению сt-критерием Стъюдента, он требует значительно меньшего объема вычислений и почти также строго проверяет нормально распределенные выборки. Его эффективность для больших и малых выборок составляет около 95%.
Если две рассматриваемые переменные имеют альтернативное распределение (включают только две градации, как например, показатели теста в группе ниже или выше некой избранной величины до и после тренировок, либо количество справившихся с контрольной по математике среди мальчиков и девочек), то подходящими непараметрическими критериями достоверности различий будут %2(хи-квадратен не рекомендован к применению, если число опытов в каждом из сравниваемых распределений меньше 10) и точный критерий Фишерадля четырехпольной таблицы. Внимание: не путайте алгоритм расчета упомянутого непараметрического критерия %2 симеющим много общего алгоритмом расчета критерия согласия х2Пирсона, полезного при сравнении эмпирического и теоретического распределений, как правило используемого для установления соответствия реально полученного распределения нормальному закону.
Для выяснения связей между признаками (корреляции) можно рассчитать уже упоминавшийся тетрахорический показатель(г),ранговые коэффициенты корреляции Спирмена(R или р) и may (т)Кендалла.Последние два могут быть использованы для определения тесноты связей как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака.
❖ Компьютерная обработка и графические иллюстрации
Пускай вас не смущает некоторая перегруженность статистических процедур, рекомендуемых для использования в дипломной работе. В большинстве случаев вам не обязательно (хотя и желательно) быть знакомыми с их математическим аппаратом. К сегодняшнему дню для нужд науки разработаны многочисленные компьютерные программы, позволяющие даже не сведущему в математике человеку довольно легко рассчитывать большинство желаемых показателей. Самыми известными и популярными из них являются пакеты Statistica (табличные и графические примеры с ее использованием приведены выше) иSPSS. Обе программы снабжены справочным материалом в формеHelp-ов и специальным информационным сопровождением с обзором основных расчетных алгоритмов. При выведении показателей различия, в корреляционных матрицах и в других таблицах автоматически выделяются цветом и жирностью числовые значения, представляющие для исследователя особый интерес (по достоверности, важности, приоритетности и т. д.).
Эти же пакеты позволяют существенно улучшить внешний вид дипломной работы за счет внесения в нее большей наглядности. Это достигается заменой некоторых трудно читаемых таблиц и цифровых данных на графики, гистограммы, и другие формы иллюстраций, хорошо вписывающихся в смысловую канву предъявленных результатов (но ничего лишнего!).
Выбор формы графика не должен быть случаен. Например, изменения во времени лучше воспринимаются в линейном представлении, сопоставление показателей двух групп - в столбчатом, пропорции - в круговых гистограммах, а рассеяние - в точечном (рис. 5—8).
