- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко математический анализ
- •Часть 3
- •Учебное пособие
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко
- •Часть 3
- •Введение
- •1. Обыкновенные дифференциальные уравнения
- •1.1. Дифференциальные уравнения первого порядка
- •1. Определение дифференциального уравнения первого порядка.
- •2. Решение уравнения. Задача Коши.
- •5. Уравнение с разделяющимися переменными.
- •6. Однородные уравнения первого порядка.
- •6. Линейные уравнения.
- •Согласно условию
- •Дифференциальные уравнения второго порядка
- •Основные понятия.
- •1.3. Линейные дифференциальные уравнения второго порядка
- •Основные понятия.
- •1.4. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Дифференцируя и подставляя в уравнение, получаем
- •Дифференцируя и подставляя в уравнение, получаем
- •1.5. Применение линейных дифференциальных уравнений к изучению колебательных явлений
- •1.6. Системы дифференциальных уравнений
- •Задачи к п. 1
- •Ответы к п. 1
- •2. Кратные интегралы
- •2.1. Двойные интегралы
- •2.3. Замена переменных в двойном интеграле
- •2.4. Некоторые геометрические и физические приложения двойных интегралов
- •Решение. Имеем
- •2. Вычисление площади. Как было установлено, площадь s области g может быть вычислена с помощью двойного интеграла по формуле
- •Задачи к п. 2.1
- •Ответы к п. 2.1
- •2.2. Тройные интегралы
- •Задачи к п. 2.2
- •Ответы к п. 2.2
- •3. Криволинейные интегралы
- •3.1. Криволинейные интегралы Вычисление криволинейных интегралов
- •Таким образом, окончательно имеем
- •Пример 6. Вычислить интеграл где:
- •3.2. Формула Грина
- •3.3. Условия независимости криволинейного интеграла от пути интегрирования
- •3.4. Интегрирование полных дифференциалов
- •Формула
- •Решение. В данном выражении функции
- •Решение. В данном случае функции
- •3.5. Некоторые приложения криволинейных интегралов второго рода
- •Задачи к п. 3
- •Ответы к п. 3
- •4. Поверхностные интегралы
- •4.1. Поверхностные интегралы. Вычисление поверхностных интегралов
- •4.2. Формула Остроградского
- •4.3. Формула Стокса
- •Задачи к п. 4
- •Ответы к п. 4
- •Библиографический список
- •Главление
- •1. Обыкновенные дифференциальные уравнения............4
- •2. Кратные интегралы ……….……………....…………......63
- •Бырдин Аркадий Петрович
- •Часть 3
- •394026 Воронеж, Московский просп., 14
2.3. Замена переменных в двойном интеграле
Пусть функция непрерывна в некоторой замкнутой ограниченной области G. Тогда для функции существует двойной интеграл
Предположим, далее, что с помощью формул
![]() ,
,
![]() (2.4)
(2.4)
мы переходим к новым переменным и и v. Будем считать, что и и v определяются из (2.4) единственным образом:
![]() ,
,
![]() .
(2.5)
.
(2.5)
С
помощью формул (2.5) каждой точке
![]() из
области G
ставится
в соответствие некоторая точка
из
области G
ставится
в соответствие некоторая точка
![]() на
координатной
плоскости с прямоугольными координатами
и
и
v.
Пусть множество всех точек
на
координатной
плоскости с прямоугольными координатами
и
и
v.
Пусть множество всех точек
![]() образует
ограниченную
замкнутую область G*.
Формулы
(2.4) называют формулами
преобразования координат,
а
формулы (2.5) формулами
обратного преобразования.
образует
ограниченную
замкнутую область G*.
Формулы
(2.4) называют формулами
преобразования координат,
а
формулы (2.5) формулами
обратного преобразования.
При сделанных предположениях можно доказать, что если функции (2.4) имеют в области G* непрерывные частные производные первого порядка и если определитель
 (2.6)
(2.6)
отличен в G* от нуля, то для интеграла (2.2) справедлива формула замены переменных
![]() .
(2.7)
.
(2.7)
Определитель (2.6) называется функциональным определителем или якобианом (по имени немецкого математика Якоби) функций , по переменным и и v. Коротко изложенное можно сформулировать в виде следующей теоремы.
Теорема 4. Если преобразование (2.5) переводит замкнутую ограниченную область G в замкнутую ограниченную область G* и является взаимно однозначным, и если функции (2.4) имеют в области G* непрерывные частные производные первого порядка и отличный от нуля якобиан (2.6), а функция непрерывна в области G, то справедлива формула замены переменных (2.7).
Как в двойном, так и в определенном интеграле замена переменных - важнейший способ приведения интеграла к виду, более удобному для вычисления.
Пример
1.
Вычислить интеграл
![]() ,
где
G
- параллелограмм, отграниченный прямыми
,
где
G
- параллелограмм, отграниченный прямыми
![]() ,
,
![]() ,
,
![]() ,
,
![]() (рис.11,а).
(рис.11,а).

а) б)
Рис. 11
Решение. Непосредственное вычисление этого интеграла достаточно громоздкое, так как для сведения его к повторному (сначала по у, а затем по х) необходимо область G разбить на три области (штриховые линии на рис.11,а) и затем вычислить соответственно три интеграла. Однако простая замена переменных
![]() ,
,
![]() (2.8)
(2.8)
позволяет
значительно упростить решение. Прямые
и
в системен координат Оху
переходят
в прямые
![]() и
и
![]() в
системе координат
в
системе координат
![]() (рис.
11, б), а прямые
и
- в
прямые
(рис.
11, б), а прямые
и
- в
прямые
![]() и
и
![]() .
Параллелограмм G
взаимно
однозначно преобразуется в прямоугольник
G*,
которым является
более простой областью интегрирования.
Осталось вычислить
якобиан. Для этого выразим х
и
у через
и
и
v
из равенств
(2.8):
.
Параллелограмм G
взаимно
однозначно преобразуется в прямоугольник
G*,
которым является
более простой областью интегрирования.
Осталось вычислить
якобиан. Для этого выразим х
и
у через
и
и
v
из равенств
(2.8):
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
 .
.
По формуле (2.7) окончательно получаем

Замечание.
Если подынтегральная функция или
уравнение
границы области интегрирования
содержат
сумму
![]() ,
то во многих случаях упрощение
интеграла достигается
преобразованием его к полярным
координатам, так
как данная сумма в полярных координатах
(
,
то во многих случаях упрощение
интеграла достигается
преобразованием его к полярным
координатам, так
как данная сумма в полярных координатах
(![]() ,
,
![]() )
принимает достаточно простой вид
)
принимает достаточно простой вид
![]() .
.
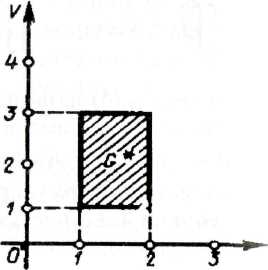
Пример
2. Вычислить
интеграл
![]() ,
где G
- четверть
круга
,
где G
- четверть
круга
![]() ,
расположенная
в первом квадранте (рис. 12).
,
расположенная
в первом квадранте (рис. 12).
Решение. Преобразуем интеграл к полярным координатам
по
формулам
,
.
Тогда
![]() и
и

Наглядно
видно, что в области
![]() изменяется
в пределах от 0 до 1, а
- от 0 до
изменяется
в пределах от 0 до 1, а
- от 0 до
![]() .
Иначе говоря,
область G
преобразуется
в прямоугольник
.
Иначе говоря,
область G
преобразуется
в прямоугольник
![]() (рис.
12).
Таким образом, по формуле
(2.5) получаем
(рис.
12).
Таким образом, по формуле
(2.5) получаем

На практике при замене переменных нет необходимости детально строить область G*. Обычно выясняют пределы изменения новых координат, используя вид области G на плоскости Оху, что и сделано вначале в данном примере.
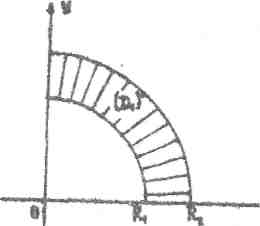
Пример
3.
Вычислить двойной интеграл
![]() по
области D,
ограниченной
линиями
по
области D,
ограниченной
линиями
![]() ,
,
![]() ,
,
и расположенной
в первом квадранте (рис. 13).
,
,
и расположенной
в первом квадранте (рис. 13).
Решение.
Уравнение внутренней окружности
(![]() )
в полярных координатах примет вид
)
в полярных координатах примет вид
![]() ,
а внешней окружности (
,
а внешней окружности (![]() )
-
)
-
![]() .
Поэтому
.
Поэтому
![]()