Ответы к п. 1

1. y = Cx, y = 2x. 2. xy = C, xy = 8. 3. 4. 5.

6. 7. 8.

9. . 10.

11. 12. 13. . 14. . 15. . 16. . 17. . 18. . 19. .

20. . 21. . 22. . 23. . 24. . 25. . 26. . 27. . 28. . 29. . 30. 31. 32. 33. 34. 35. 36. 37. y = 1. 38. 39. 40.

41. 42. 43.

44. 45. 46.

47. 48.

49. 50.

51. 52. 53.

54. 55. 56.

57. 58. 59.

60. 61. 62.

63. 64. 65. . 66. . 67. .

68. . 69. .

70. . 71. .

72. 73. .

74. 75. .

76. 77. .

78. . 79. .

80. 81. .

82. 83. .

84. 85.

86. 87.

88. 89.

90. 91.

92. 93.

94. 95.

96. . 97.

98. 99.

100. 101.

102.

103.

104.

105.

106.

107.

108.

109.

110.

111.

112.

113.

114.

115.

116.

117.

118.

119. 120.

121. 122.

123. 124.

125. 126.

127. 128.

129. 130.

131. 132.

133. 134.

135. 136.

137. 138.

139. 140.

141.

142.

143.

144.

145.

146.

147.

148.

149.

150.

151.

152.

153.

154.

155.

156.

157.

158.

159.

160.

161.

162.

163.

164.

165.

166.

167.

168.

2. Кратные интегралы

2.1. Двойные интегралы

Двойной интеграл представляет собой обобщение понятия опре­деленного интеграла на случай функций двух переменных.

1. Определение и условия существования двойного интеграла. Пусть G  некоторая замкнутая ограниченная область, a  произвольная функция, определенная и ограниченная в этой области.

Рис.

П

Рис. 8

Рис. 5

редполагается, что граница об­ласти G состоит из конечного числа кривых, заданных уравнениями вида или , где f(x) и  непрерывные функции. Такой областью, например, является зам­кнутый многоугольник, граница ко­торого состоит из конечного числа отрезков, представляющих собой графики непрерывных функций вида или . Другой пример  область, ограниченная эллипсом (здесь граница состоит из двух кривых: ) и т. д.

Разобьем область G произвольно на п частей не имеющих общих внутренних точек, с площадями (рис. 5). В каждой части выберем произвольную точку и составим сумму

(2.1)

которую назовем интегральной суммой для функции f(x,у) в области G. Назовем диаметром d(G) области G наибольшее рас­стояние между граничными точками этой области. Обозначим через наибольший из диаметров частичных областей

Определение. Если интегральная сумма (2.1) при имеет предел, равный I, то этот предел называется двойным интегралом от функции по области G и обозначается одним из сле­дующих символов:

В этом случае функция называется интегрируемой в области G, G  областью интегрирования, х и у  переменными интегриро­вания, (или dxdy)  элементом площади.

Давая определение двойного интеграла, мы предполагаем, что функция ограничена. Как и для функции одной переменной, это условие является необходимым условием интегрируемости. Однако оно не является достаточным, т. е. существуют ограничен­ные, но не интегрируемые функции. Примером таких функций является функция, определенная на квадрате следующим образом:

Доказательство неинтегрируемости такой функции непосредственно следует из определения двойного интеграла.

Теорема 1. Функция , непрерывная в замкнутой ограниченной области G, интегрируема в этой области.

Однако не следует считать, что двойной интеграл существует только для непрерывных функций. Имеет место более общая тео­рема.

Теорема 2. Функция , ограниченная в замкнутой ограниченной области G и непрерывная в ней всюду, кроме точек, лежащих на конечном числе кривых, являющихся графиками непре­рывных функций вида или , интегрируема в этой области.

2

Рис. 6

. Геометрический смысл двойного интеграла. Пусть в прост­ранстве дано тело Р (рис. 6), ограниченное сверху графиком непрерывной и неотрицательной функции , которая опре­делена в области G, с боков  цилиндрической повер-хностью, направляющей которой служит граница области G, а образующие параллельны оси Оz, и снизу областью G, лежащей в плоскости Оху. Тело такого вида называют криволиней-ным цилиндром.

Аналогично тому, как задача о вычислении площади криволи­нейной трапеции приводит к установлению геометрического смысла определенного интеграла, так и задача о вычислении объема тела Р приводит к геометрическому толкованию двойного интеграла.

Действительно, в данном случае интегральная сумма (2.1) пред­ставляет собой сумму объемов прямых цилиндров с площадями оснований и высотами , которую можно принять за приближенное значение объема тела Р:

Это приближенное равенство тем точнее, чем мельче разбиение области G на части. При переходе к пределу при это приб­лиженное равенство становится точным:

Так как функция интег­рируема, то предел интегральной суммы существует и равен двой­ному интегралу от этой функции по области G. Следовательно,

Отсюда следует геометрический смысл двойного интеграла: двойной интеграл от непрерывной, неотрицательной функции равен объему криволинейного цилиндра.

Замечание. Если положить =1 всюду в области G то непосредственно из определения двойного интеграла получим выражение площади s области G в виде двойного интеграла:

3. Свойства двойного интеграла. Основные свойства двойного интеграла аналогичны соответствующим свойствам определенного интеграла.

1°. Если - произвольное число и функция интегри­руема в области G, то функция тоже интегрируема в G и , т.е. постоянный множитель можно выносить за знак интеграла.

2°. Если функции и интегрируемы в области G, то их сумма также интегрируема в этой области и

.

3°. Если область G является объединением областей и , не имеющих общих внутренних точек, в каждой из которых функция интегрируема, то в области G эта функция также интегрируема и

.

4°. Теорема о среднем. Если функция непрерывна в области G, то в этой области найдется такая точка , что , где s –площадь G.

Итак, рассмотрены определение и основные свойств; двойного интеграла, условия существования, выяснен en геометрический смысл. Теперь рассмотрим способы вычисления двойных интегралов.

Рис. 7

Рис. 8

2.2. Сведение двойного интеграла к повторному

Теорема 3. Пусть функция определена в области G= , где и непрерывные функции, для (pис.7). Пусть также существует двойной интеграл и для каждого х из отрезка существует определенный интеграл . Тогда существует повторный интеграл 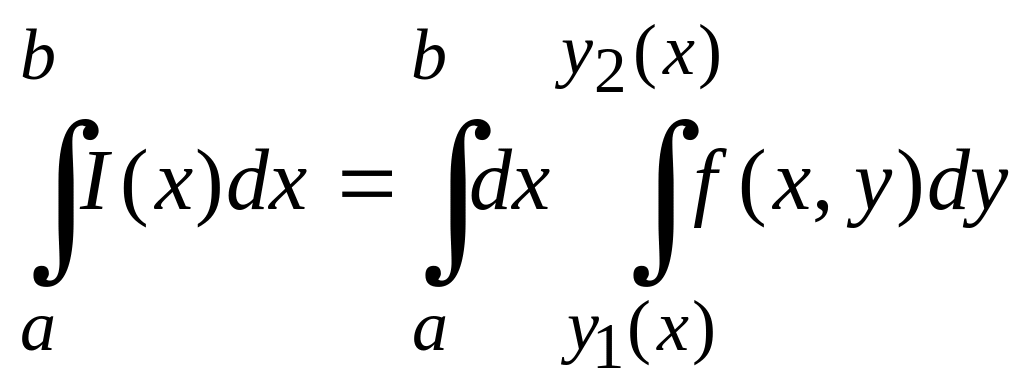и справедливо равенство

. (2.2)

З а м е ч а н и е 1. Если в теореме 3 поменять ролями x и y, то теорема будет утверждать существование повторного интеграла и равенства

. (2.3)

Пример 1. Вычислить интеграл по области G= .

Решение. Область G представляет собой треугольник, ограниченный осями координат и прямой (рис. 8).Следовательно, , . По формуле (2.2) имеем

Данный интеграл можно вычислить и по формуле (2.3), если в G поменять х и у ролями. Тогда треугольник определяется неравенствами , откуда , , и легко проверить, что интеграл:

имеет то же самое значение.

Рис. 9

П ример 2. Вычислить двойной интеграл по области D ограниченной параболой и прямой (рис.9). Решение. Применим формулу (2.2). Переменная изменяется от значения на нижней кривой до значения на верхней кривой . При этом изменяется от абсциссы точки ­ до абсциссы точки пересечений и . Решая систему уравнений

получим координаты точек O(0;0), A(1;1). Таким образом x меняется от 0 до 1 ( ). По формуле (2.2) получим:

Пример 3. Изменить порядок интегрирования в повторном интеграле .

Решение. Область интегрирования ограничена прямыми , , кубической параболой и параболой (рис. 10).

Рис. 10

Определим пределы интегрирования. Решая систему уравнений , получим - нижний предел интегрирования по , - верхний предел. Чтобы найти пределы изменения по во внутреннем интеграле, выразим через из уравнения кривой, которая ограничивает область интегрирования слева ( ) получим , а из уравнения кривой, которая ограничивает область справа, получим . Поэтому справедливо равенство

Замечание 2. Если область G не удовлетворяет условиям теоремы 3 (например, вертикальные или горизонтальные прямые пересекают ее границу более чем в двух точках), то необходимо область G разбить на части каждая из которых удовлетворяла бы условиям теоремы 3, и сводить к повторному каждый из соответствующих двойных интегралов отдельно.