Формула

(3.18)

где  фиксированная точка, а С  произвольная постоян­ная, и дает возможность определить все функции, имеющие подын­тегральное выражение своим полным дифференциалом.

Для отыскания F(x, у) по формуле (3.18) достаточно, выбрав любую точку в области G, вычислить криволинейный инте­грал по любой кривой, соединяющей точки и . Так как в формуле (3.18) интеграл не зависит от выбора пути, то удобно, например, за путь интегрирования взять ломаную, звенья которой параллельны осям координат (рис. 39). Тогда

Так как и на участке от до , a на участке от до то равенство (3.18) принимает вид 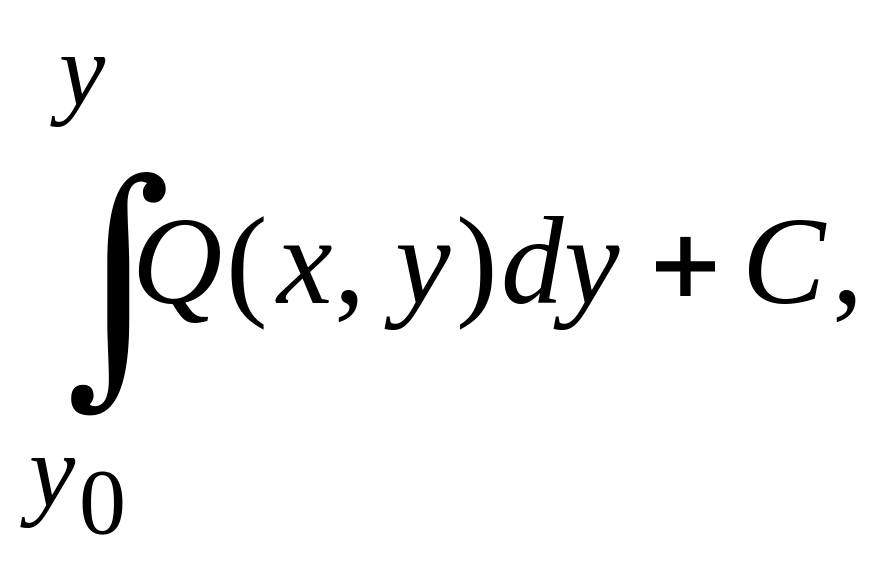где первый определенный интеграл вычисляется при постоянном у, равном , а второй  при постоянном х.

Пример 1. Проверить, является ли выражение полным дифференци-алом некоторой функции , и, если это так, найти .

Решение. В данном выражении функции

Р(х, у) = , Q(х, у) = (3.19)

непрерывны вместе с частными производными которые равны между собой. Следовательно, данное выражение является полным дифференциалом некоторой функции . Для отыскания функции воспользуемся формулой (3.15), где  некоторая фиксированная точка, а В(х; у)  переменная точка.

В данном случае за точку удобно взять точку (0;0). Учитывая, что криволинейный интеграл не зависит от пути интегрирования, выбе­рем путь интегрирования от точки (0;0) до точки (х;у) в виде ло­маной, звенья которой параллельны осям координат. Для этого достаточно взять точку (х;0) [или точку (0;у)] (рис. 40).

Тогда одно звено ломаной будет лежать на оси координат. Имеем

где С  произвольная постоянная.

Практически при отыскании функции по ее полному дифферен­циалу удобно поступать следующим образом. Если

то, интегрируя первое из этих равенств по х, получаем

(3.20)

а интегрируя второе равенство по у, имеем

(3.21)

где и  произвольные функции. Если подобрать функ­ции и так, чтобы правые части равенств (3.20) и (3.21) сов­пали, то полученная таким образом функция и является функцией, полный дифференциал которой совпадает с выражением .

Так, например, пусть Ин­тегрируя коэффициент при dx по х, получаем

(3.22)

интегрируя коэффициент при dy по у, имеем

(3.23)

Правые части равенств (3.22) и (3.23) совпадают, если положить

Таким образом,

Пример 2. Вычислить криволинейный интеграл

Решение. В данном случае функции

непрерывны и частные производные равны между собой. Значит, выражение является полным дифференциалом и данный интеграл не зависит от пути интегрирования. По форму­лам (3.20) и (3.21) находим , и по формуле (3.17) получаем

Заметим, что данный интеграл можно вычислить и непосред­ственно, если, например, взять в качестве пути интегрирования ломаную, соединяющую точки (1;2), (2;2) и (2;3), звенья ко­торой параллельны осям координат.