Задачи к п. 2.1

Вычислить двойные интегралы по областям G, ограниченным указанными линиями:

1.

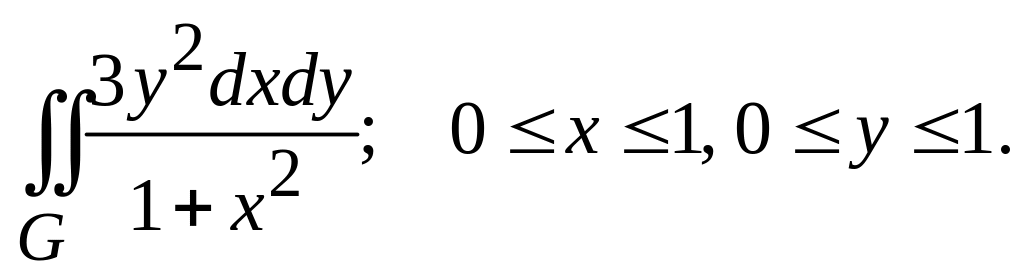
2.

3.

4.

5.

6.

7.

8.

9. 0

10.

11. G – круг радиуса R с центром в начале координат.

12. G – треугольник с вершинами О (0; 0), В(0; 1), А(1; 1).

13. область, ограниченная осью Ox и аркой циклоиды

14. область, ограниченная осями координат и частью астроиды

Вычислить следующие интегралы, перейдя к полярным координатам:

15. половина круга радиуса R с центром в начале координат, лежащая в области

16. четверть круга располо-женная в первом квадранте.

17. круг радиуса R c центром в начале координат.

18. круг

19. кольцо между окружностями радиусов е и 1 с центром в начале координат.

Вычислить объемы тел, ограниченных поверхностями:

20.

21.

22.

23.

24.

25.

26.

27.

Перейдя к полярным координатам, вычислить объемы тел, ограниченных поверхностями:

28.

29.

30.

Вычислить площади областей, ограниченных линиями:

31.

32.

33.

34.

Перейдя к полярным координатам, найти площади фигур, ограниченных линиями:

35. .

36.

37.

38.

39. Вычислить площадь той части плоскости которая заключена в первом октанте.

40. Вычислить площадь боковой поверхности кругового конуса с радиусом основания R и высотой H.

41. Вычислить площадь части плоскости отсекаемой плоскостями

42. Вычислить площадь части плоскости вырезаемой цилиндром

Найти координаты центра масс однородной пластинки, ограниченной линиями:

43. Двумя параболами и

44. y = 0 и одной полуволной синусоиды .

45.

46.

Вычислить момент инерции однородной пластинки, ограниченной линиями:

47. относительно оси Ox.

48. относительно оси Oy.

49. относительно оси Ox.

Ответы к п. 2.1

1. 2. 3. . 4. . 5. . 6. 7. 8. 9. 10. . 11. 0. 12. 13. . 14. . 15. 16. 17. 18. . 19. 2. 20. . 21. . 22. 23. 24. 25. . 26. 27. . 28. 29. 30. 31. . 32. 33. 34. . 35. 36. 37. 38. 39. 14. 40. 41. 42. 43. 44. 45. (3; 4; 8). 46. 47. 48. 49. 4.

2.2. Тройные интегралы

В предыдущем разделе было введено понятие двойного интеграла от функции двух переменных. Определим интеграл от функции трех переменных  так называемый тройной интеграл. Тройные интегралы, как и двойные, имеют широкое применение в различных физических и геометрических задачах.

1. Определение тройного интеграла. Тройной интеграл явля­ется аналогом двойного интеграла и вводится для функции трех переменных.

Пусть в некоторой замкнутой ограниченной области V трех­мерного пространства задана ограниченная функция . Разобьем область V на п произвольных областей, не имеющих общих внутренних точек, с объемами . В каждой области возьмем произвольную точку и составим сумму

(2.14)

которая называется интегральной суммой для функции f(x, у, z) по области V. Обозначим через наибольший из диаметров частич­ных областей.

Определение. Если интегральная сумма (2.14) при имеет предел, равный I, то этот предел называется тройным интегра­лом от функции f(x, у, z) по области V и обозначается одним из следующих символов:

В этом случае функция называется интегрируемой в об­ласти V; V  областью интегрирования; х, у и z  переменными интегрирования; (или dx dy dz)  элементом объема.

В дальнейшем, поскольку результаты, полученные для двой­ных интегралов, вместе с их доказательствами могут быть пере­несены на тройные интегралы, ограничимся только формулиров­ками утверждений и краткими пояснениями.

Тройные интегралы являются непосредственным обобщением двойных интегралов на случай трехмерного пространства. Они обладают аналогичными двойным интегралам необходимыми и до­статочными условиями существования и свойствами. Если поло­жить всюду в области V то из определения тройного интеграла следует формула для вычисления объема тела V:

2. Вычисление тройных интегралов. Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычисле­нию интегралов меньшей кратности.

Рассмотрим область V, ограниченную снизу и сверху поверх­ностями и а с боковых сторон цилин­дрической поверхностью, и пусть область G  проекция области V на плоскость Оху (рис. 21), в которой определены и непрерывны функции и Предположим, далее, что каждая прямая, параллельная оси пересекает границу области V не более чем в двух точках. Тогда для любой функции , непрерывной в области V, имеет место формула

позволяющая свести вычисление тройного интеграла к последова­тельному вычислению внутреннего определенного интеграла по переменной z (при постоянных х и у) и внешнего двойного инте­грала по области G. Выражение

представляет собой функцию двух переменных. Если для этой функ­ции и области G, по которой она интегрируется, выполнены ус­ловия теоремы 2, то, переходя от двойного интеграла к повторному, получаем формулу

(2.15)

сводящую вычисление тройного интеграла к последовательному вычислению трех определенных интегралов. Порядок интегриро­вания может быть и другим, т.е. переменные х, у и z в формуле (2.15) можно менять ролями.

В частности, если V  параллелепипед с гранями , , , ( ), , ( ), то фор­мула (2.15) принимает вид

(2.16)

Пример 1. Вычислить интеграл где V  параллелепипед, ограниченный плоскостями (рис. 22).

Решение. По формуле (2.16) имеем

П ример 2. Вычислить интеграл где V  пирамида, ограниченная плоскостью и координат­ными плоскостями (рис. 23).

Решение. Область V проектируется на плоскость Оху в тре­угольник G, ограниченный прямыми По формуле (2.16) имеем

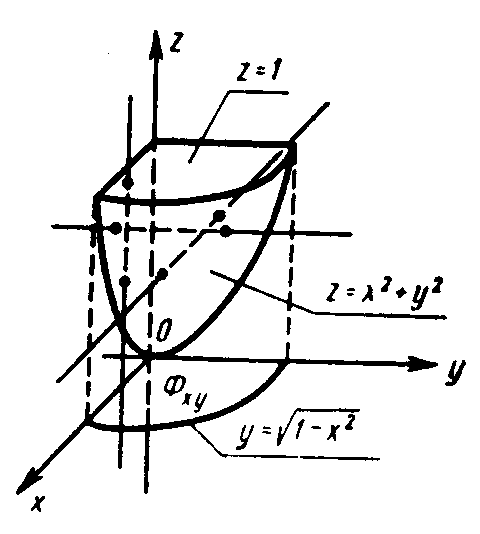
Пример 3. Вычислить где область ограничена поверхностями , , , (рис. 24).

Решение. По формуле (2.16) получим

=

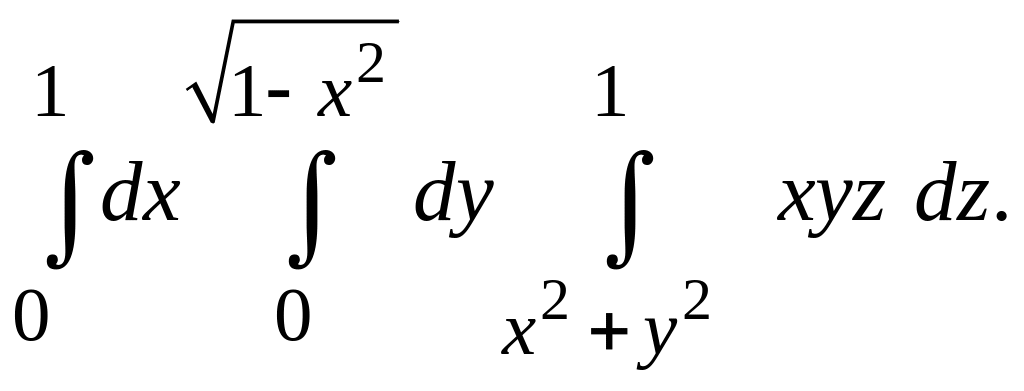
Вычислим кратный интеграл последовательно:

1) ;

2. ;

3. .

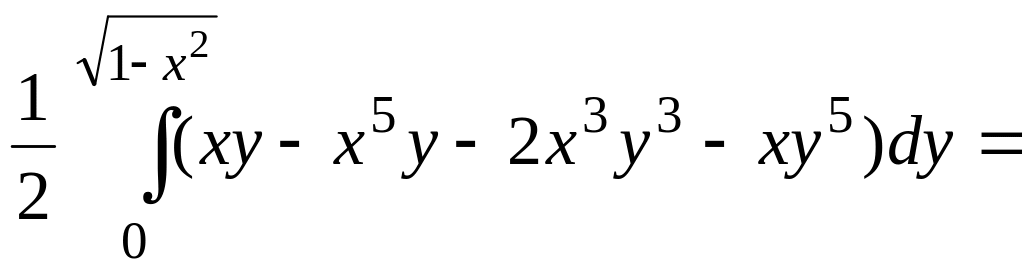
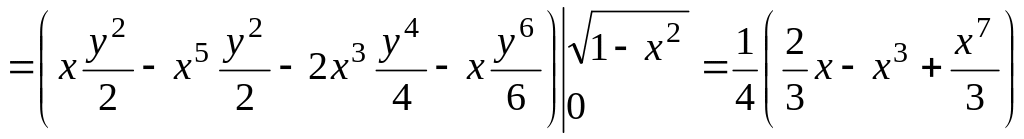Рис. 24

3. Замена переменных в тройном интеграле. Как для двойных интегралов, так и для тройных имеют место формулы перехода от прямоугольных координат к новым системам координат, наиболее употребительными из которых являются цилиндрические и сфери­ческие координаты.

Замену переменных в тройном интеграле производят по сле­дующему правилу. Если ограниченная замкнутая область V пространства взаимно однозначно отображается на область V* пространства с помощью непрерывно дифференцируемых функций , , и якобиан J в области V* не обращается в нуль:

то справедлива формула

В частности, при переходе от прямоугольных координат х, у, z к цилиндрическим координатам (рис. 25), связанным с х, у, z формулами якобиан преобразования , поэтому

(2.17)

Название “цилиндрические координаты” связано с тем, что коор­динатная поверхность (т. е. поверхность, все точки которой имеют одну и ту же координату ) является цилиндром, прямолинейные образующие которого параллельны оси Оz.

При переходе от прямоугольных координат х, у, z к сфериче­ским координатам (рис. 26), связанным с х, у, z формулами

якобиан преобразования поэтому

(2.18)

Название «сферические координаты» связано с тем, что коор­динатная поверхность является сферой. Сфе­рические координаты иначе называют полярными координатами в пространстве.

П ри вычислении тройного интеграла путем перехода к цилин­дрическим или сферическим координатам область V* обычно не изображают, а пределы интегрирования расставляют непосред­ственно по виду области V, используя геометрический смысл но­вых координат.

Пример 4. Вычислить интеграл перехо­дом к цилиндрическим координатам , где V  область, ограниченная поверхностями и z = 1 (рис. 27).

Решение. Так как область V на плоскость Оху проектиру­ется в круг , то координата изменяется в пределах от 0 до , координата  от = 0 до = 1. Постоянному зна­чению в пространстве Охуz

соответствует цилиндр . Рассматривая пересечение этого цилиндра с об­ластью V, получаем изменение координаты z от значений для то­чек, лежащих на параболоиде , до значений для точек, лежащих на плоскости , т. е. от до . Применяя формулу (2.17), имеем

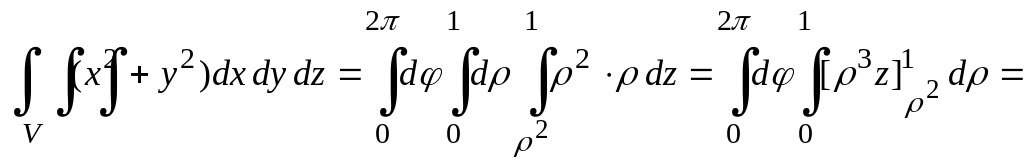
Трудно дать какую-либо общую рекомендацию, когда следует применять ту или иную систему координат. Это зависит и от обла­сти интегрирования, и от вида подынтегральной функции. Однако, например, формулой (2.18) удобнее пользоваться, когда имеет вид , а также когда областью V является шар или его часть.

Пример 5. Вычислить интеграл

где V  шар (рис. 28).

Решение. В данном случае удобно перейти к сферическим координатам:

.

Из вида области V следует, что координаты , и меняются в следующих пределах:  от 0 до R,  от 0 до ,  от 0 до . Так как подынтегральная функция

то по формуле (2.18) получаем

П

Рис. 29

ример 6. Вычислить тройной интеграл где область интегрирования V есть восьмая часть шара , расположенная в первом октанте (рис. 29).

Решение. Перейдем к сферическим координатам. Новые переменные будут изменяться в области V в пределах , , . Применяя формулу (2.18), получим

=

4. Некоторые приложения тройных интегралов. Кратко рас­смотрим типичные задачи применения тройных интегралов, огра­ничившись приведением необходимых формул, так как их вывод аналогичен выводу соответствующих формул в случае двойных интегралов.

Если дано некоторое тело V с плотностью представляющей собой непрерывную функцию, то тройной интеграл представляет собой массу т данного тела.

Моменты инерции тела V с плот­ностью относительно осей координат определяются следую­щими формулами:

Момент инерции относительно начала координат

Координаты центра масс определяются следующими форму­лами:

где  координаты центра масс, а т  масса данного тела. В частности, если рассматриваемое тело однородно, т. е. то выражения для координат центра масс упрощаются и принимают вид

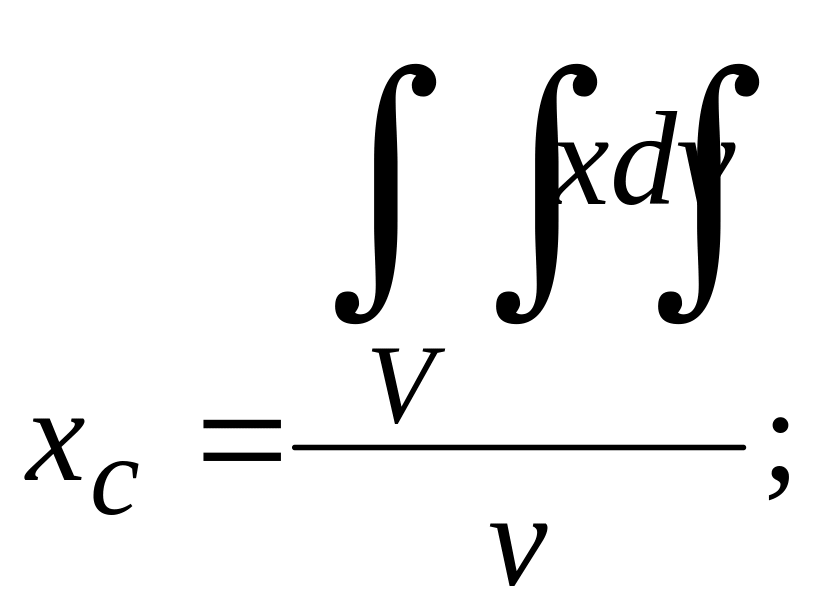
где v  объем данного тела.

Как уже было отмечено, тройной интеграл равен объему тела V. Тройные интегралы в некоторых случаях более удобны для вычисления объемов, чем двойные, так как с их по­мощью можно вычислить объем не только криволинейного цилин­дра, но и других тел.

Пример 7. Определить координаты центра масс верхней поло­вины однородного шара V радиуса R с центром в начале коорди­нат.

Решение. Данный полушар ограничен поверхностями и . В силу симметрии полушара Координата определяется по формуле

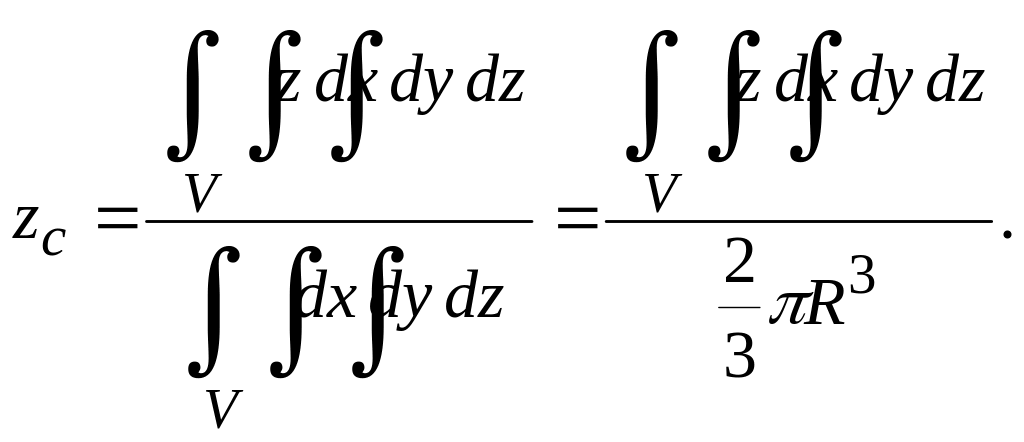
Переходя к сферическим координатам, получаем

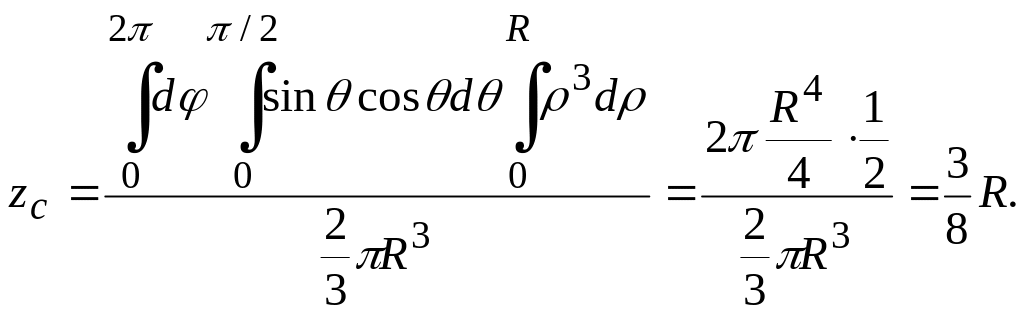
Пример 8. Определить момент инерции относительно оси OZ однородной пирамиды с плотностью равной 3, ограниченной плоскостями , , , (рис. 30).

Решение. Имеем

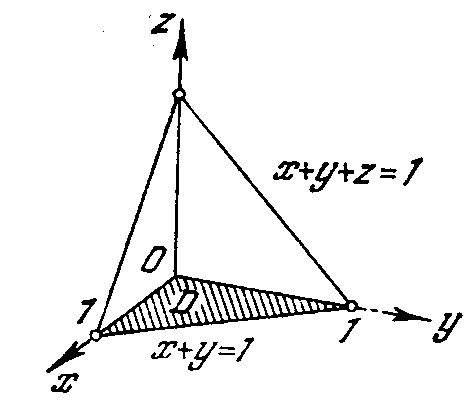
Рис. 30