Задачи к п. 2.2

Вычислить тройные интегралы по областям V, ограниченным указанными поверхностями:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

С помощью замены переменных вычислить тройные интегралы:

15. шар.

16.

17.

18.

19. часть шара , находя-щаяся в первом октанте.

20.

21.

22.

Вычислить объемы тел, ограниченных указанными поверхностями:

23.

24.

25.

26.

27.

28.

29.

30.

Ответы к п. 2.2

1. 2. 2. . 3. . 4. . 5. 6. 54. 7. 54. 8. . 9. . 10. 0. 11. . 12. . 13. 14. 15. 16. 17. 18. 8. 19. . 20. . 21. . 22. 24. 23. 12. 24. 25. 26. 4

27. 28. . 29. . 30. .

3. Криволинейные интегралы

3.1. Криволинейные интегралы Вычисление криволинейных интегралов

Обобщим понятие определенного интеграла на случай, когда областью интегрирования является отрезок некоторой кривой, лежащей в плоскости.

Интегралы такого рода называются криволинейными. Они имеют широкое применение в различных разделах математики.

Различают два типа криволинейных интегралов: криволинейные интегралы первого и второго рода.

1. Определение криволинейного интеграла первого рода. Рас­смотрим на плоскости Оху некоторую кривую АВ, гладкую или кусочно-гладкую, и предположим, что функция опре­делена и ограничена на кривой АВ.

Разобьем кривую АВ произвольно на п частей точками , выберем на каж­дой из частичных дуг произвольную точку (рис. 31) и составим сумму

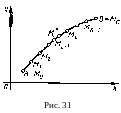(3.1)

где  длина дуги . Сумма (3.1) называется интеграль­ной суммой для функции , по кривой АВ. Обо­значим через наибольшую из длин частичных дуг

Определение. Если интегральная сумма (3.1) при имеет предел, равный I, то этот предел называется криволинейным интегралом первого рода от функции по кривой АВ и обозначается одним из сле­дующих символов

В этом случае функция называется интегрируемой вдоль кривой АВ, сама кривая АВ  контуром интегрирования, А  начальной, а В  конечной точками интегрирования.

Криволинейный интеграл первого рода легко сводится к опре­деленному интегралу. Действительно, приняв на кривой АВ за параметр длину дуги l, отсчитываемую от точки A, получим пара­метрическое представление кривой , . При этом функция , заданная вдоль АВ, становится сложной функцией параметра l:f[x(l), y(l)]. Обозначив через значение параметра l, отвечающее точке , а через  отвечаю­щее точке , перепишем интегральную сумму (1.1) в виде

(3.2)

где и Сумма (3.2) является интеграль­ной для определенного интеграла от функции f[x(l), y(l)] на от­резке [0, L]. Поскольку интегральные суммы (3.1) и (3.2) равны между собой, равны и соответствующие им интегралы, т. е.

(3.3)

Заметим, что формула (3.3) не только выражает криволинейный ин­теграл через определенный, но и доказывает существование кри­волинейного интеграла от функции , непрерывной вдоль рассматриваемой кривой АВ.

Как было показано, криволинейный интеграл первого рода не­посредственно сводится к определенному, однако между этими понятиями имеется следующее различие. В интегральной сумме (3.1) величины обязательно положительны, независимо от того, какую точку кривой АВ считать начальной, а какую  конеч­ной, т. е.

в то время как определенный интеграл при перестановке пределов интегрирования меняет знак. В остальном криволиней­ный интеграл первого рода обладает теми же свойствами, что и оп­ределенный интеграл. Это непосредственно вытекает из формулы (3.3).

К риволинейный интеграл первого рода, так же как и определен­ный, имеет геометрический смысл. Если определенный интеграл при представляет собой площадь криволинейной трапеции, то криволинейный интеграл при численно равен площади куска цилиндрической поверхности, ко­торая составлена из перпендикуляров к плоскости Оху, восстанов­ленных в точках кривой АВ и имеющих переменную длину (рис. 32).

В частности, если АВ  не кривая, а отрезок прямой [а, b], расположенный на оси Ох, то , и криволи­нейный интеграл будет обычным определенным интегралом.

Если положить , то получим криволиней­ный интеграл значение которого есть длина дуги кривой АВ.

Таким образом, с помощью криволинейного интеграла первого рода можно вычислять площадь цилиндрических поверхностей и длины дуг. Кроме этого, криволинейный интеграл первого рода имеет широкое применение в физике. С его помощью можно, как это делали в случае двойных интегралов, находить массу материальной кривой по ее плотности, моменты инерции относительно координатных осей, координаты центра масс такой кривой и т. д.

2. Вычисление криволинейных интегралов первого рода. Вы­числение криволинейных интегралов первого рода сводится к вы­числению определенных интегралов.

Пусть кривая АВ задана параметрически уравнениями где и  непрерывные вместе со своими производными и функции, a f(x,у)  функция, непрерывная вдоль этой кривой, причем для определен­ности будем считать, что точке A соответствует значение точке В  значение . Тогда для любой точки М ( ; ) кривой АВ длину l дуги AM можно рассматривать как функцию параметра t: , и вычислять ее по формуле откуда, согласно правилу дифферен­цирования интеграла по верхнему пределу,

(3.4)

Заменяя переменную в определенном интеграле в пра­вой части равенства (3.3) и учитывая (3.4), получаем

(3.5)

Пример 1. Вычислить криволинейный интеграл где АВ  часть окружности .

Решение. Так как

то по формуле (3.5) получаем

В частности, если кривая АВ задана уравнением , , где  непрерывно дифференцируемая функция, то, принимая х за параметр ( ), из формулы (3.5) имеем

(3.6)

Пример 2. Вычислить криволинейный интеграл где AB  дуга параболы от точки (0; 0) до точки (2; 2).

Решение. Имеем

По формуле (3.6) получаем

З а м е ч а н и е. Формула (3.4) представляет самостоятельный интерес. Возводя в квадрат, получаем: . Это равенство дает простое геометри­ческое истолкование дифференциала дуги dl. Учитывая, что диф­ференциал функции равен при­ращению ординаты касательной, получаем, что дифференциал дуги dl (см. рис. 39) равен длине от­резка касательной к кривой АВ от точки касания с абсциссой х до точки ( ), т.е. гипотенузе прямоугольного треугольника с катетами и , а равенство пред­ставляет собой теорему Пифагора.

Рассмотрим теперь случай пространственной кривой АВ. Пусть параметрические уравнения пространственной гладкой кривой АВ имеют вид , , , причем существуют непрерывные производные , , .

предположим, что параметр t изменяется в пределах

  t   ( < ). Тогда справедлива формула

. (3.7)

Пример 3. Вычислить x + y + z) dl по дуге витка винтовой линии, заданной параметрически уравнениями , , при .

Решение. По формуле (3.7) находим

3. Определение криволинейного ин­теграла второго рода. Пусть на кривой АВ определены две ограниченные фун­кции Р(х, у) и Q(x, у). Разобьем кривую АВ на п частей точками . Обозначим через и проекции вектора на оси координат (рис. 33). На каж­дой частичной дуге возьмем произвольную точку и сос­тавим интегральную сумму для функции Р(х, у) [Q(х,у)]:

(3.8)

Определение. Если интегральная сумма (3.8) при ( ,  длина дуги ) имеет предел, равный I, то этот предел называется криволинейным интегралом вто­рого рода от функции Р(х, y)[Q (х, у)] по кривой АВ и обозначается символом

Сумму

называют общим криволинейным интегралом второго рода и обоз­начают символом

.

К риволинейные интегралы второго рода, как и интегралы пер­вого рода, легко сводятся к определенным интегралам.

Действительно, пусть кривая АВ задана параметрически урав­нениями где и непре­рывные вместе со своими производными и функции, причем точке А кривой соответствует значение , точке В — значение Пусть функции и непрерывны вдоль кривой АВ. Тогда справедливы следую­щие формулы:

(3.9)

сводящие криволинейные интегралы к определенным интегралам. Криволинейный интеграл второго рода обладает свойствами, аналогичными свойствам определенного интеграла, что непосред­ственно вытекает из формул (3.9).

В отличие от криволинейного интеграла первого рода криволи­нейный интеграл второго рода зависит от того, в каком направле­нии (от А к В или от В к A) проходится кривая AB, и меняет знак при изменении направления обхода кривой, т. е.

Действительно, изменив направление обхода кривой, мы со­ответственно изменим знаки проекций и в суммах (3.8), и, следовательно, сами суммы и их пределы изменят знак.

Таким образом, при вычислении криволинейных интегралов второго рода необходимо учитывать направление интегрирования.

В случае, когда L замкнутая кривая, т. е. когда точка В сов­падает с точкой A, из двух возможных направлений обхода зам­кнутого контура L условимся называть положительным то направ­ление, при котором область, лежащая внутри этого контура, оста­ется слева по отношению к точке, совершающей обход. Противо­положное направление обхода контура L условимся называть отрицательным.

Криволинейный интеграл по замкнутому контуру L, пробегае­мому в положительном направлении, часто обозначают символом

4. Вычисление криволинейных интегралов второго рода. Кри­волинейные интегралы второго рода вычисляют сведением их к оп­ределенным интегралам по формулам (3.9). В частности, если кривая АВ задана уравнением вида , , где у(х)  непрерывно дифференцируемая функция, то, принимая х за параметр (t=x), из формул (3.9) полу­чаем

(3.10)

Аналогичные формулы имеют место, если кривая АВ задана урав­нением вида .

Пример 4. Вычислить интеграл , где АВ  четверть окружности , А соответствует , В соответствует .

Решение. Имеем . По третьей из формул (3.9) получаем

Пример 5. Вычислить интеграл где L  контур прямоугольника, образованного прямыми , , и (рис. 34).

Решение. На рис. 34 положительное направление обхода контура L обозначено стрелками. Разбивая весь контур интегри­рования на части, запишем:

Легко заметить, что интегралы вдоль участков АВ и CD равны нулю, так как на них у является постоянным и, следовательно, . Поэтому остается вычислить интегралы по участкам ВС и DA. По формуле, аналогичной первой из формул (3.10) [заменяя х на у и у(х) на х(у)], получаем