Ответы к п. 3

1. 2. 3. 4.

5. . 6. 7. 8. 1) 4; 2) 10/3; 3) 2. 9. 1) 8; 2) 4. 10. 8. 11. 2. 12. 2. 13. . 14. 8. 15. 4/3. 16. 2/3. 17. 18. 19. 221/15. 20. . 21. 22. 23. 24. 25. 26. 27. 28. 29. 2/3. 30. 0. 31. , где - коэффициент пропорциональности. 32. . 33.

4. Поверхностные интегралы

4.1. Поверхностные интегралы. Вычисление поверхностных интегралов

В этом параграфе будут рассмотрены интегралы от функций, задан­ных на поверхности, так называемые поверхностные интегралы.

Теория поверхностных интегралов во многом аналогична тео­рии криволинейных интегралов. Различают поверхностные инте­гралы первого и второго рода.

1. Определение поверхностного интеграла первого рода. Пусть в точках некоторой поверхности S гладкой или кусочно-гладкой определена ограниченная функция . Разобьем поверхность S произвольно на п частей с площадями (рис. 42). Выбрав на каждой частичной поверхности произвольную точку составим сумму

(4.1)

Сумма (4.1) называется интегральной суммой для функции f (М) по поверхности S. Обозначим через наибольший из диаметров частей поверхности.

Определение. Если интегральная сумма (4.1) при имеет предел, равный I, то этот предел называется поверхностным инте­гралом первого рода от функции по поверхности S и обо­значается одним из следующих символов: В этом случае функция называется интегрируемой по поверхности S, а S  областью интегрирования.

Рис.31

Рис. 32

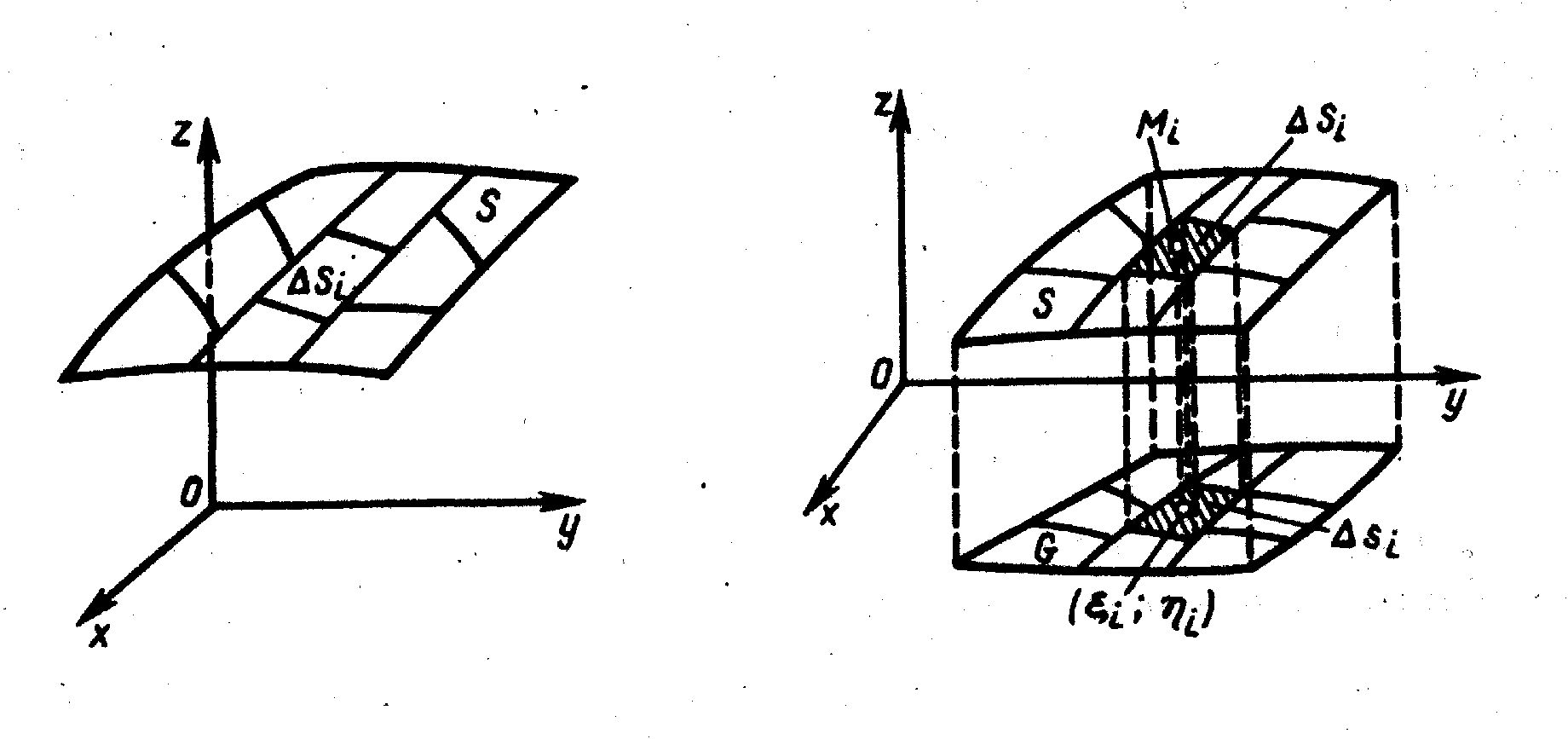Рис. 42 Рис. 43

Данное определение по сути аналогично определению двой­ного интеграла. Поэтому свойства двойных интегралов и условия их существования без особых изменений переносятся на поверх­ностные интегралы.

В частности, если на поверхности S, то где s  площадь поверхности S, т.е. с помощью поверхностного интеграла первого рода можно вычислять площади поверхностей.

Кроме того, с их помощью можно определять массы, статиче­ские моменты, моменты инерции, координаты центра масс и по­добные величины для материальных поверхностей с известной поверхностной плотностью распределения масс. Эти задачи ре­шаются аналогично соответствующим задачам для случая матери­альной кривой, материальной плоской и пространственной обла­сти.

2. Вычисление поверхностных интегралов первого рода. Вы­числение поверхностного интеграла первого рода производится сведением поверхностного интеграла к двойному.

Пусть поверхность S задана уравнением , где функ­ция вместе с производными и непрерывна в замкнутой области G — проекции S на плоскость Оху (рис. 43), и пусть функция непрерывна на поверхности S и, следо­вательно, интегрируема по этой поверхности. В этом случае справедлива формула

выражающая поверхностный интеграл первого рода через двойной по проекции поверхности S на плоскость Оху.

Аналогично получаются формулы, выражающие интеграл по поверхности S через двойные по ее проекциям на плоскости Оуz и Охz.

П ример 1. Вычислить интеграл где S  часть параболоида вращения отсеченного плоскостью (рис. 44).

Решение. Поверхность S, заданная уравнением проектируется на плоскость Оху в область G, ограничен­ную окружностью (уравнение окружности получается из уравнения параболоида при ). Следовательно, областью G является круг В этом круге функции непре­рывны. По формуле (4.2) получаем

Переходя в полученном двойном интеграле к полярным координа­там , находим

3. Определение поверхностного интеграла второго рода. Введем предварительно понятие стороны поверхности.

Возьмем на гладкой поверхности S произвольную точку М и проведем через нее нормаль к поверхности (вектор ). Рассмо­трим теперь на поверхности S какой-либо замкнутый контур, про­ходящий через точку М и не имеющий общих точек с границей поверхности S. Будем перемещать точку М по замкнутому кон­туру вместе с вектором так, чтобы вектор все время оставался нормальным к S и чтобы его направление менялось при этом пе­ремещении непрерывно (рис. 45). В начальное положение точка М вернется либо с тем же направлением нормали, либо с противопо­ложным.

Если обход по любому замкнутому контуру, лежащему на по­верхности S и не пересекающему ее границы, при возвращении в исходную точку не меняет направления нормали к поверхности, то поверхность называется двусторонней.

Примерами двусторонних поверхностей служат плоскость, сфе­ра, любая поверхность, заданная уравнением где и  функции, непрерывные в некоторой области G плоскости Оху.

Если же на поверхности S существует замкнутый контур, при обходе которого направление нормали меняется после возвращения в исходную точку на противоположное, то поверхность называется односторонней.

Простейшим примером односторонней поверхности служит лист Мёбиуса, изображенный на рис. 46. Его можно получить, взяв полоску бумаги ABCD и склеив ее так, чтобы точка А совпала с точкой С, а точка В  с точкой D, т. е. повернув перед склеива­нием один из ее краев на 180°. При обходе листа Мёбиуса по его средней линии и возвращении в исходную точку направление нор­мали меняется на противоположное.

В дальнейшем рассматриваются только двусторонние поверх­ности. Для двусторонней поверхности совокупность всех ее точек с выбранным в них направлением нормали, изменяющимся непре­рывно при переходе от точки к точке, называется стороной поверх­ности, а выбор определенной ее стороны  ориентацией поверх­ности. Двустороннюю поверхность называют также ориентируе­мой, а одностороннюю  неориентируемой.

С понятием стороны поверхности тесно связано понятие ориен­тации ее границы.

Пусть S  ориентированная (сторона уже выбрана) поверх­ность, ограниченная контуром L, не имеющим точек самопересе­чения. Будем считать положительным направлением обхода кон­тура L то, при движении по которому наблюдатель, расположен­ный так, что направление нормали совпадает с направлением от ног к голове, оставляет поверхность слева от себя (рис.47). Противоположное направление обхода называется отрицатель­ным. Если изменить ориентацию поверхности, т. е. изменить направление нормали на противоположное, то положительное и отрицательное направления обхода контура L поменяются ролями.

Перейдем теперь к определению поверхностного интеграла вто­рого рода. Пусть S  гладкая поверхность, заданная уравнением , и ограниченная функция, определенная в точках поверхности S. Выберем одну из двух сторон поверхно­сти, т. е. одно из двух возможных направлений нормали в точках поверхности (тем самым мы ориентировали поверхность). Если нормали составляют острые углы с осью Оz, то будем говорить, что выбрана верхняя сторона поверхности , если тупые углы, то нижняя сторона поверхности. Разобьем поверхность S произвольно на п частей и обозначим через проекцию i-й части поверхности на плоскость Оху. Выбрав на каждой частичной по­верхности произвольную точку , составим сумму

(4.3)

где ,  площадь взятая со знаком плюс, если выбрана верх­няя сторона поверхности S, и со знаком минус, если выбрана ниж­няя сторона поверхности S (рис. 48). Сумма (4.3) называется интегральной суммой для функции . Обозначим через наи­больший из диаметров частей поверхности S.

Определение. Если интегральная сумма (4.3) при имеет предел, равный I, то этот предел называется поверхностным инте­гралом второго рода от функции по выбранной стороне поверхности S и обозначается одним из следующих символов:

В этом случае функция называется интегрируемой по поверхности S по переменным х и у.

Аналогично определяется поверхностный интеграл второго рода по выбранной стороне поверхности S по переменным у и z (z и х) от функции ( ), которая определена на поверх­ности S:

Сумму

называют общим поверхностным интегралом второго рода и обоз­начают символом

(4.4)

Поверхностный интеграл второго рода обладает такими же свойствами, как и поверхностный интеграл первого рода, но в от­личие от последнего при изменении стороны поверхности (пере­ориентации) он меняет знак.

К понятию поверхностного интеграла второго рода приводит, например, задача о потоке векторного поля, которая будет рас­смотрена в дальнейшем.

Для односторонней поверхности понятие поверхностного инте­грала второго рода не вводится.

4. Вычисление поверхностных интегралов второго рода. По­верхностные интегралы второго рода вычисляют сведением их к двойным интегралам. Пусть ориентированная (выберем верхнюю сторону) гладкая поверхность S задана уравнением где функция определена в замкнутой области G  проекции поверхности S на плоскость Оху, а  непрерывная функция на по­верхности S .

Формула, выражающая поверхностный интеграл второго рода по перемен­ным х и у через двойной, имеет вид

(4.5)

Кроме того, формула (4.5) доказывает су­ществование поверхностного интеграла от функции , непрерывной на рассматриваемой поверхности S. Если выбрать нижнюю сторону поверхности, то перед интегралом в правой ча­сти (4.5) появится знак минус. Аналогично устанавливается справедливость следующих фор­мул:

(4.6)

(4.7)

где поверхность S задана соответственно уравнением и а и  проекции поверхности S соответственно на плоскости Оуz и Охz.

Для вычисления интеграла общего вида (4.4) используют те же формулы (4.5)  (4.7), если поверхность S однозначно проектиру­ется на все три координатные плоскости. В более сложных слу­чаях поверхность S разбивают на части, обладающие указанными свойствами, а интеграл (4.4)  на сумму интегралов по этим частям.

П ример 2. Вычислить интеграл где S  верхняя сторона поверхности отсеченная плоско­стями (рис. 49).

Решение. Проекцией G данной поверхности на плоскость Оху является прямоугольник, определяемый неравенствами . По формуле (4.5) находим

Пример 3. Вычислить интеграл где S  верхняя сторона части плоскости , отсе­ченная плоскостями и лежащая в первом октанте (рис. 50).

Решение. По определению,

З десь и  проекции поверхности S на плоскости Оуz и Оху, а так как плоскость S параллельна оси Оу. По формулам (4.5) и (4.6) соответственно находим

Следовательно,

5. Связь между поверхностными интегралами первого и второго рода. Поверхностные интегралы второго рода можно ввести и дру­гим способом, а именно как поверхностные интегралы первого рода, в которых под знаком интег­рала стоят некоторые специальные выражения. Обозначим через направляющие косинусы нормали ориентированной поверх­ности в произвольной ее точке. По­верхностные интегралы второго рода различаются своим отношением к координатным плоскостям:

1) поверхностный интеграл вто­рого рода для плоскости Оху от функции выражается через поверхностный интеграл первого рода с помощью следующей формулы:

(4.8)

2) поверхностный интеграл второго рода для плоскости Охz от функции выражается через поверхностный интеграл первого рода с помощью следующей формулы:

(4.9)

3) поверхностный интеграл второго рода для плоскости Оуz от функции выражается через поверхностный интеграл первого рода с помощью следующей формулы:

(4.10)

Суммируя формулы (4.8)  (4.10), получаем формулу, выражаю­щую поверхностный интеграл второго рода общего вида по выбран­ной стороне поверхности через поверхностный интеграл первого рода:

Если выбрать другую сторону поверхности, то направляющие ко­синусы нормали и изменят знак и, следовательно, изменит знак поверхностный интеграл второго рода.

Пример 4. Вычислить интеграл , где S  внешняя сторона полусферы расположенной над плоско­стью Оху, а  острый угол между нормалью к поверхности S с осью Оz (рис. 51).

Р ешение. По формуле (4.8), свя­зывающей поверхностные интегралы обоих типов, имеем

Проекцией G данной поверхности S на плоскость Оху является круг По формуле (4.5) получаем

Переходя к полярным координатам, находим