2.4. Некоторые геометрические и физические приложения двойных интегралов

1. Вычисление объема. Как известно, объем v криволинейного цилиндра, ограниченного сверху поверхностью , снизу плоскостью и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси , а направляющей служит контур области G, вычисляется по формуле , т.е. с помощью двойных интегралов можно вычислять объемы тел.

Пример 1. Вычислить объем тела, ограниченного поверхностями , , и (рис. 14).

Решение. Имеем где G  треугольная область интегрирования, ограниченная пря­мыми . Расставляя пределы интегрирова­ния в двойном интеграле, получаем

Рис. 14 Рис. 15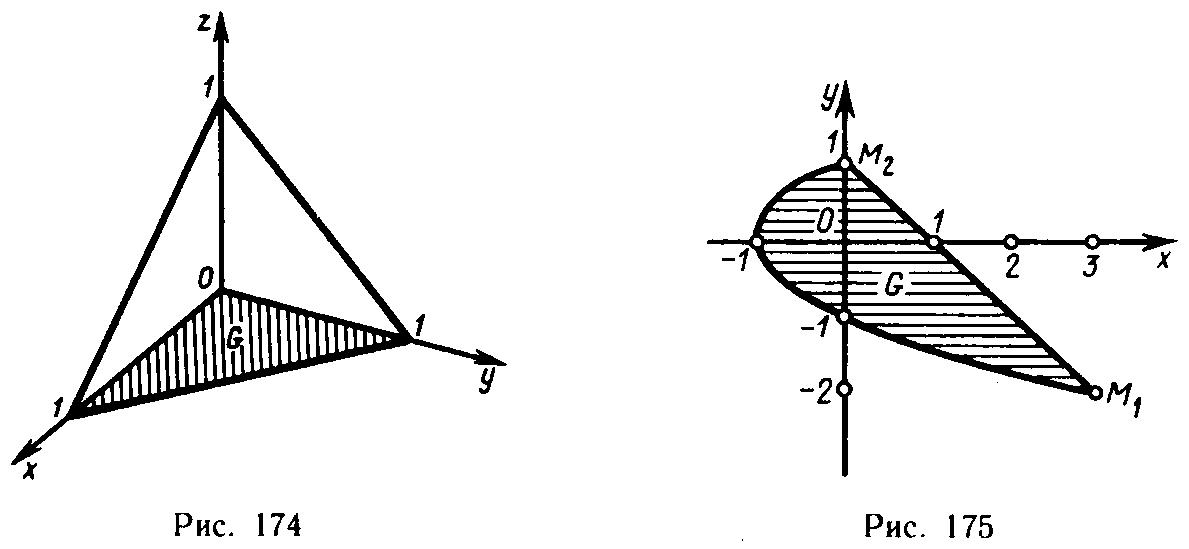

Пример 2. Найти объем v тела, ограниченного параболоидом , цилиндром и плоскостями и (рис. 16).

Рис. 16

Решение. Имеем

2. Вычисление площади. Как было установлено, площадь s области g может быть вычислена с помощью двойного интеграла по формуле

Эта формула более универсальна, чем соответствующая формула, выражающая площадь криволинейной трапеции с помощью опреде­ленного интеграла, так как данная формула применима не только к криволинейным трапециям, но и к фигурам, расположенным произвольно по отношению к координатным осям.

Пример 3. Вычислить площадь области G, ограниченной ли­ниями (рис. 15).

Решение. Область G представляет собой фигуру, ограни­ченную слева параболой справа прямой . Решая совместно уравнения параболы и прямой, находим точки их пересечения: . Следовательно, искомая площадь

При вычислении двойных интегралов с помощью повторного интегрирования одним из главных моментов является расстановка пределов интегрирования. Если в данном примере выбрать другой порядок повторного интегрирования (сначала по у, а затем по х), то область G предварительно пришлось бы разбить на две части (осью Оу), так как она ограничена сверху линией, заданной на отрезках и двумя различными уравнени­ями. Разумеется, был бы получен тот же результат, однако вычис­ления оказались бы более громоздкими.

Поэтому полезно запомнить следующее правило: если все пря­мые, параллельные оси Оу, входят в область интегрирования G на линии, заданной одним уравнением, и выходят из области на линии, заданной одним уравнением, то внутренний интеграл целе­сообразно брать по переменной у, а внешний  по х; аналогично, если все прямые, параллельные оси Ох, входят в область интегриро­вания на линии, заданной одним уравнением (в данном случае на параболе), и выходят на линии, заданной одним уравнением (в дан­ном случае на прямой), то внутренний интеграл следует брать по переменной х, а внешний  по у: в этом случае область интегриро­вания не нужно разбивать на части.

3. Вычисление площади поверхности. С помощью двойных ин­тегралов можно вычислять площади не только плоских фигур, но и кривых поверхностей.

П усть поверхность S задана уравнением , проек­цией S на плоскость Оху является область G (рис. 17) и в этой области функция непрерывна и имеет непрерывные част­ные производные и .

Формула, с помощью которой вычисляется площадь поверхности, имеет вид

(2.9)

Пример 4. Вычислить площадь той части плоскости , которая заключена в первом октанте (рис. 18).

Решение. Так как функция и область G, являющаяся проекцией данной части поверхности на плоскость Оху, удовлетворяют сформулированным выше условиям, то иско­мую площадь можно вычислить по формуле (2.9). Имеем

;

Областью G является треугольник, ограниченный осями Ox, Оу и прямой , получаемой из уравнения данной плоскости при . Расставляя пределы интегрирования в двой­ном интеграле, получаем

4. Вычисление массы пластинки. Рассмотрим на плоскости Оху материальную пластинку, т. е. некоторую область G, по которой распределена масса m с плотностью (х, у). Вычислим по задан­ной плотности массу т этой пластинки, считая, что  непрерывная функция. Разобьем G произвольно на п частей и обозначим через массы этих частей. В каждой части произвольно возьмем точку . Массу каждой такой части можно считать приближенно равной , где  площадь , а масса т всей пластинки приближенно равна сумме которая является интегральной суммой для непрерывной функ­ции области G. В пределе при очевидно, получим точное значение массы пластинки, равное двойному интегралу от функции (х, у) по области G, т. е.

(2.10)

Пример 5. Определить массу квадратной пластинки со сторо­ной 2а, если плотность (х, у) в каждой точке М(х; у) пропор­циональна квадрату расстояния от точки М до точки пересечения диагоналей, и коэффициент пропорциональности равен k.

Решение. Выберем систему координат так, как показано на рис. 19. После этого можно найти функцию (х, у) исходя из условия задачи. Пусть  произвольная точка квадрат­ной пластинки. Тогда квадрат расстояния от точки М до точки пересечения диагоналей равен Следовательно, плотность в точке М

По формуле (2.10) имеем

Учитывая, что подынтегральная функция четна относительно х и у, а область интегрирования симметрична относительно осей координат, можно ограничиться вычислением интеграла по той части области G, которая расположена в первой четверти, т. е.

5. Вычисление координат центра масс пластинки. Найдем коор­динаты центра масс пластинки, занимающей в плоскости Оху не­которую область G. Пусть - плотность этой пластинки в точке , причем -непрерывная функция. Раз­бив область G на части , выберем в каждой из этих частей некоторую точку и будем приближенно считать массу каждой из частей пластинки равной ( - площадь ). Если считать, что каждая из этих масс сосредоточена в одной точке, а именно в точке , то для координат и центра масс такой системы материальных точек получим следую­щие выражения:

(2.11)

которые представляют собой приближенные значения координат центра масс пластинки. Чтобы получить точные значения этих ко­ординат, необходимо в (2.11) перейти к пределу при При этом интегральные суммы перейдут в соответствующие интегралы и мы получим, что координаты центра масс пластинки определяются формулами

(2.11а)

где  масса пластинки.

Если пластинка однородна, т. е. то формулы коор­динат центра масс упрощаются:

(2.12)

Величины и

в формулах (2.11а) называются статическими моментами пластинки отно­сительно осей Оу и Ох.

Т аким образом, вычисление координат центра масс пластинки сводится к вычислению трех двойных интегралов.

Пример 6. Найти координаты центра масс однородной пла­стинки, ограниченной двумя параболами и (рис. 20).

Решение. Координаты центра масс данной пластинки найдем по фор­мулам (2.12). Сначала вычислим массу пластинки

Далее вычислим ее статические моменты относительно осей коор­динат:

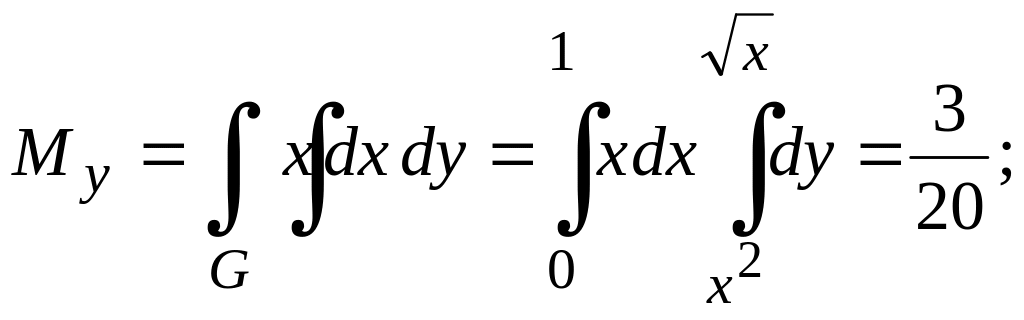
Затем по формулам (2.12) найдем

Итак,

6. Вычисление момента инерции пластинки. Как известно, мо­мент инерции материальной точки относительно некоторой оси равен произведению массы точки на квадрат ее расстояния до этой оси, а момент инерции системы материальных точек равен сумме моментов инерции этих точек.

Пусть область G плоскости Оху занята пластинкой, имеющей непрерывную плотность . Разбив область G на части , площади которых равны , и выбрав в каждой из них некоторую точку , заменим пластинку системой материальных точек с массами и координатами . Момент инерции такой системы точечных масс, например, относительно оси Оу равен . Примем это выра­жение за приближенное значение момента инерции пластинки. Но оно же представляет собой интегральную сумму для непрерыв­ной функции Переходя к пределу при получаем для момента инерции пластинки относительно оси Оу следующую формулу:

Аналогично, момент инерции пластинки относительно оси Ох равен

Найдем момент инерции пластинки относительно начала ко­ординат. Принимая во внимание, что момент инерции материаль­ной точки с массой т относительно начала координат равен , рассуждая, как и выше, получаем, что

(2.13)

Пример 7. Найти момент инерции круга радиуса R с постоян­ной плотностью относительно начала координат.

Решение. По формуле (2.13) имеем

Перейдем к полярным координатам. Уравнение окружности (гра­ницы круга) в полярных координатах имеет вид . Поэтому