1.6. Системы дифференциальных уравнений
Метод исключения. Для нахождения решения системы двух дифференциальных уравнений вида
(1.58)
разрешенной относительно производных от искомых функций y и z, дифференцируем по x одно из них. Имеем, например:
(1.59)
Определяя z из первого уравнения системы (1.58) и подставляя найденное выражение
(1.60)
в уравнение (1.59), получим уравнение второго порядка с одной неизвестной функцией y. Решая его, находим:
(1.61)
где
и
произвольные
постоянные. Подставляя функцию (1.61) в
формулу (1.60), определяем функцию z.
Совокупность формул (1.60) и (1.61), где y
заменено на ,
дает общее решение системы (1.58).
Задача
Коши для системы (1.58) состоит в том, чтобы
найти такое решение системы (1.58), которое
при
принимало бы заданные значения:
Пример. Решить задачу Коши для системы
Решение.
Выразим из первого уравнения z
через y и x:
После подстановки этого выражения во
второе уравнение будем иметь
Следовательно, для нахождения неизвестной
функции y получено
дифференциальное уравнение
второго порядка с постоянными
коэффициентами. Решая его, найдем
Тогда
В
результате получено общее решение
данной системы. Используя начальные
условия, получим для определения
постоянных
и
уравнения
откуда
Таким образом, решением данной задачи
Коши являются функции
Задачи к п. 1
В
следующих уравнениях: 1) найти общие
решения уравнений; 2) найти частные
решения по начальному условию
при
1.
2.
3.
4.
Найти общие решения уравнений:
5.
6.
7.
8.
9.
10.
11.
12.
Найти общие решения уравнений
13.
.
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
21.
.
22.
.
23.
.
24.
.
25.
.
26.
.
27.
.
28.
. 29.
.
Найти частные решения уравнений, удовлетворяющие указанным начальным условиям:
30.
при
31.
при
32.
при
33.
при
34.
при
35.
при
36.
при
37.
при
38.
при
39.
при
40.
при
Найти общие решения уравнений:
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
Решить уравнения Бернулли:
57.
58.
59.
60.
61.
62.
63.
64.
Найти общее решение дифференциального уравнения:
65.
. 66.
.
67.
. 68.
.
69.
.
70.
.
71.
. 72.
.
73.
. 74.
.
75.
. 76.
.
77.
.
78.
.
79.
. 80.
.
81.
. 82.
.
83.
. 84.
.
Решить уравнения:
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
.104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
146.
147.
148.
149.
150.
151.
152.
153.
154.
155.
156.
157.
158.
Решить системы уравнений:
159.
160.
161.
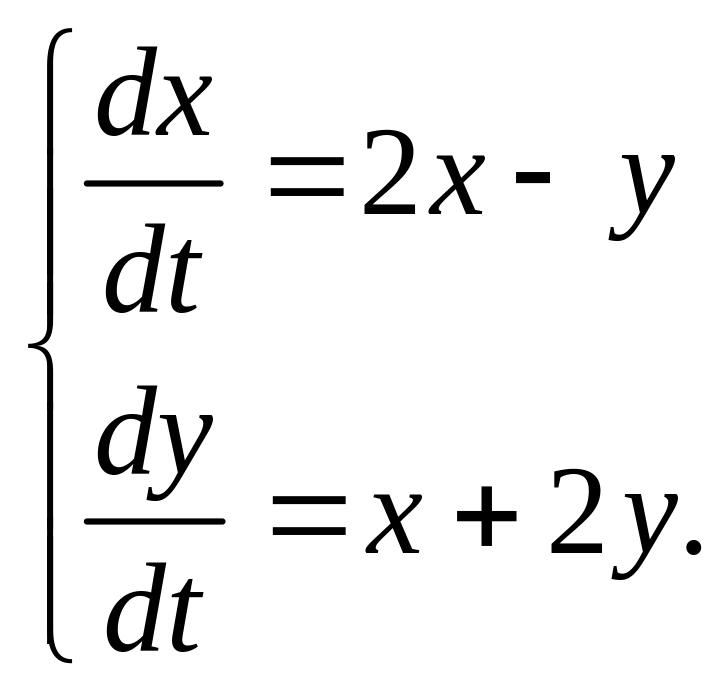
162.
163.
164.
165.
166.
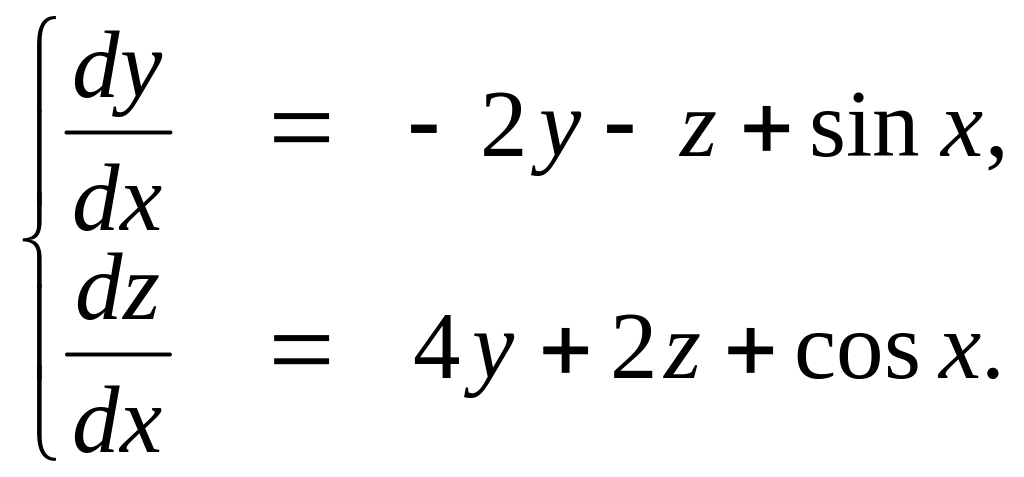
167.
168.
