4.4. Электромагнитные волны

Электромагнитной волной называется распространение возмущений электромагнитного поля в вакууме или в среде в отсутствие источников.

Существование электромагнитных волн следует из теории Максвелла, в которой утверждается, что переменное электрическое поле порождает переменное магнитное поле, а переменное магнитное поле порождает переменное электрическое поле.

Фарадей установил, что любое изменение индукции В магнитного поля вызывает появление в окружающем пространстве индукционного электрического поля, напряженность которого пропорциональна скорости изменения индукции магнитного поля:

Е ≈ .

Линии напряженности этого поля замкнуты, поэтому его называют вихревым полем. Касательная к линии напряженности индукционного электрического поля перпендикулярна вектору магнитной индукции в данной точке пространства, следовательно, вектор В и вектор Е взаимно перпендикулярны (рис. 54).

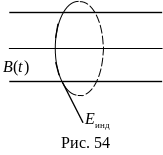
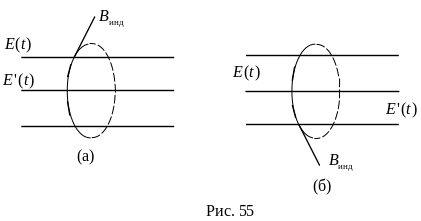
Максвелл предположил, что любое изменение напряженности Е электрического поля сопровождается возникновением вихревого магнитного поля, индукция которого пропорциональна скорости изменения напряженности электрического поля:

В ≈ .

Линии магнитной индукции этого поля замкнуты, они расположены вокруг линий напряженности переменного электрического поля точно так же, как вокруг проводников с электрическим током (рис. 55, а, б).

Согласно гипотизе Максвелла однажды начавшийся в некоторой точке пространства процесс изменения электромагнитного поля будет далее непрерывно захватывать все новые и новые области окружающего пространства. Распространяющееся переменное электромагнитное поле и есть электромагнитная волна.

В случае однородной изотропной среды уравнения Максвелла имеют вид:

rot E = - ∂B/∂t,

rot Н = ∂D/∂t,

div D = 0,

div B = 0,

где D = ε₀∙ε∙E, B = μ₀∙μ∙H и откуда получается, что ∂D/∂t = ε₀∙ε∙∂Е/∂t, а ∂В/∂t = μ₀∙μ∙∂Н/∂t. Из уравнений максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа:

∆Е = ,

∆H = ,

где ∆ = ∂²/∂x² + ∂²/∂y² + ∂²/∂z² – оператор Лапласа, v = – скорость распространения электромагнитных волн, конечная величина, определяемая электрическими и магнитными свойствами среды, в которой распространяется электромагнитная волна. Если электромагнитная волна распространяется в вакууме, то ε = 1, μ = 1 и получается, что ее скорость v равна скорости света в вакууме:

с = = = 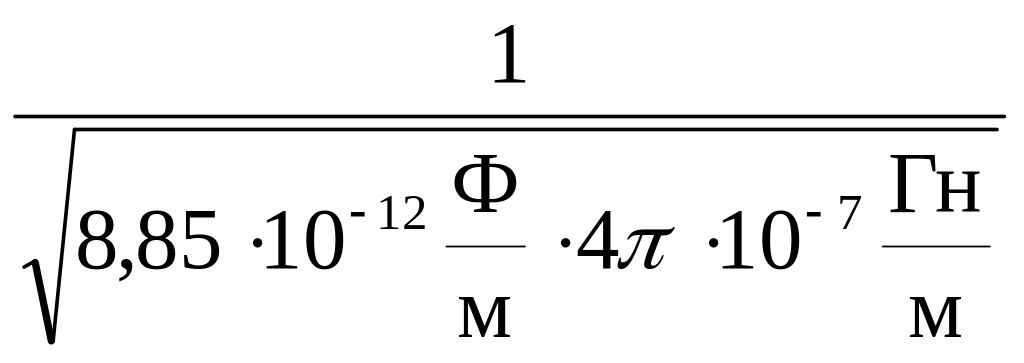3 ∙ 10⁸ .

Таким образом, электромагнитное возмущение в среде распространяется со скоростью:

v = ,

где n = – показатель преломления среды.

Решениями волновых уравнений для Е и Н являются плоские (волновые поверхности равных фаз - плоскости) монохроматические (распространяющиеся с определенной частотой, например, вдоль оси x) электромагнитные волны (Е_x = Е_z = 0, Н_x = Н_z = 0), описываемые уравнениями:

E_y = E₀sin(ωt + φ₀),

H_y = H₀sin (ωt + φ₀),

где E₀, H₀ – амплитуды векторов Е и Н, а φ₀ - начальные фазы одинаковые, так как колебания электрического и магнитного векторов напряженности в электромагнитной волне происходят с одинаковой фазой.

Плоская бегущая электромагнитная волна обладает следующими свойствами:

1. Электромагнитная волна поперечна: векторы Е и Н взаимно перпендикулярны, то есть (Е, Н) = 0, и лежат в плоскости, перпендикулярной вектору v – скорости распространения волны (рис. 56).

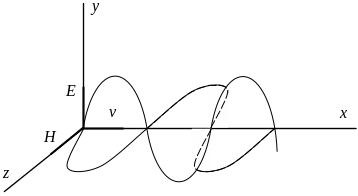
Рис. 56

Векторы Е, Н, v образуют правовинтовую систему, то есть направление векторного произведения [Е, Н] совпадает с направлением распространения волны.

2. Величины векторов Е и Н в каждый момент времени (мгновенные значения) связаны соотношением:

E∙ = H∙ (или Е = v∙В).

Под энергией электромагнитного поля подразумевается сумма энергий электрического и магнитного полей: W = W_э + W_м, а под объемной плотностью энергии соответственно сумма объемных плотностей энергий электрического и магнитных полей:

w = w_э + w_м = + = 2 w_э = ε₀∙ε∙Е²,

где учитывается, что электрическая и магнитная составляющие электромагнитного поля равноправны и в каждый момент времени w_э = w_м. После преобразования получается следующее выражение для объемной плотности энергии электромагнитного поля:

w = ε₀∙ε∙Е² = Е∙Н∙ = ∙Е∙Н.

Так как Е  Н, то вектор плотности потока электромагнитной энергии можно представить как векторное произведение Е и Н, обозначив вектором

S = [Е, Н],

называемым вектором Умова – Пойнтинга, который направлен в сторону распространения электромагнитной волны, а модуль его S = w∙v равен энергии, переносимой электромагнитной волной за единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны.

Различные виды электромагнитных волн (радиоволны, инфракрасное излучение, видимый свет, ультрафиолетовое, рентгеновское и гамма - излучение) имеют общую электромагнитную природу. Электромагнитные волны имеют очень широкий диапазон частот (от 3∙10⁵ Гц до 5∙10¹⁹ Гц ) или длин (от 10³ м до 6 ∙ 10^-12 м) волн. Скорость различных видов электромагнитных волн в пространстве одинакова и равна скорости света с в данной среде, а отличаются они друг от друга только длиной волны  = , где  - частота излучения, а с – скорость света.