3.5. Поток и циркуляция вектора магнитной индукции

Теорема Остроградского – Гаусса для магнитного поля свидетельствует о непрерывности и замкнутости магнитных силовых линий, и об отсутствии в природе магнитных зарядов.

Магнитный поток. Поток dФ_м вектора магнитной индукции В через малую поверхность с вектором элементарной площади dS = n·dS, в пределах которой вектор В можно считать неизменным, выражается, по определению (см. разд. 1.7), произведением величины площади поверхности dS и проекции В_n вектора индукции на нормаль n к этой поверхности (рис. 31):

dФ_м = (В, dS) = В·dS·cosα = В_n·dS,

где α – угол между векторами В и n. Магнитный поток Ф_м через конечную поверхность S определяется интегрированием по всей поверхности:

Ф_м = dФ_м = В_n·dS.

Магнитный поток Ф_м – скалярная величина, определяющая число силовых линий вектора В, пересекающих данную поверхность. При этом, в месте выхода силовых линий из объема V, ограниченного замкнутой поверхностью S, нормальная составляющая вектора В_n к данному участку поверхности dS считается положительной, то есть В_n>0, и элементарный поток вектора индукции через поверхность dS также положительный dФ_м>0, а в месте входа магнитных силовых линий в объем, соответственно, В_n<0 и dФ_м<0.

Интегральная форма теоремы Остроградского - Гауссадля магнитного поля показывает, что поток Ф_м вектора магнитной индукции В через любую замкнутую поверхность S, охватывающую объем V, всегда равен нулю:

Ф_м = В_n·dS = 0.

Равенство нулю интеграла по замкнутой поверхности означает (по аналогии со случаем в электростатике, когда замкнутая поверхность не охватывает электрический заряд), что число магнитных силовых линий, выходящих из ограниченного этой поверхностью объема, равно числу магнитных силовых линий, входящих в этот объем.

Из вышесказанного можно сделать вывод, что силовые линии магнитного поля (линии вектора В) всюду непрерывны и замкнуты.

Магнитный поток в СИ измеряется в веберах (Вб).

Теперь устремим объем V к нулю, стягивая ограничивающую его поверхность S к интересующей нас точке магнитного поля. По аналогии с электростатикой дифференциальная форма теоремы Остроградского – Гаусса для магнитного поля имеет вид:

div B = lim 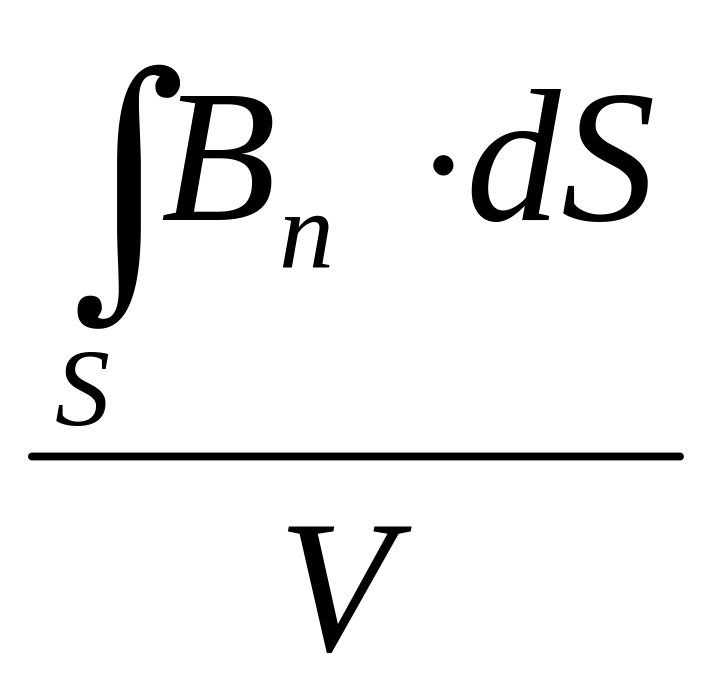= 0.

Таким образом, дивергенция В магнитного поля всюду равна нулю. Это означает, что магнитное поле не имеет магнитных источников и магнитных зарядов в природе не существует.

Теорема о циркуляции. Из закона Био-Савара-Лапласа можно вывести утверждение, что циркуляция вектора индукции В магнитного поля в вакууме, создаваемого проводниками любой формы с токами _i, вдоль любого замкнутого контура L, охватывающего эти проводники с токами, определяется алгебраической суммой токов ∑_i, охватываемых этим контуром (то есть суммарным током  = ∑_i, проходящим через натянутую на контур поверхность S):

(В, dL) = В·dL·cosα = В_L·dL = μ₀∑_i,

где α – угол между векторами В и dL, dL – вектор элементарной длины контура, направленный по току, который считается положительным, если его направление связано с направлением обхода контура правилом правого буравчика, а ток противоположного направления считается отрицательным.

Если ток непрерывно распределен по поверхности проводников, охватываемых контуром, с некоторой плотностью j, то:

В_L·dL = μ₀ d = μ₀ j_n·dS.

В векторном виде интегральная форма теоремы о циркуляции вектора В записывается выражением:

(В, dL) = μ₀ (j, dS),

где положительное направление нормали n к поверхности S определяется движением правого буравчика при его вращении в направлении обхода контура L, dS = n·dS - вектор элементарной площади dS.

Тот факт, что циркуляция вектора В не равна нулю, означает, что магнитное поле не потенциально. Ему нельзя приписать скалярный потенциал, поскольку он был бы неоднозначным.

Представим данную теорему в дифференциальной форме. Рассмотрим отношение циркуляции вектора В к площади ∆S, ограниченной плоским контуром L. При стягивании контура в точку, площадь плоской поверхности стремится к нулю ∆S→0, а искомое отношение стремится к пределу, величина которого равна вектору, называемому ротором поля вектора В и обозначаемому rot В, на направление нормали к плоскости контура в данной точке. Направление нормали n согласуется с направлением обхода контура по правилу буравчика:

lim 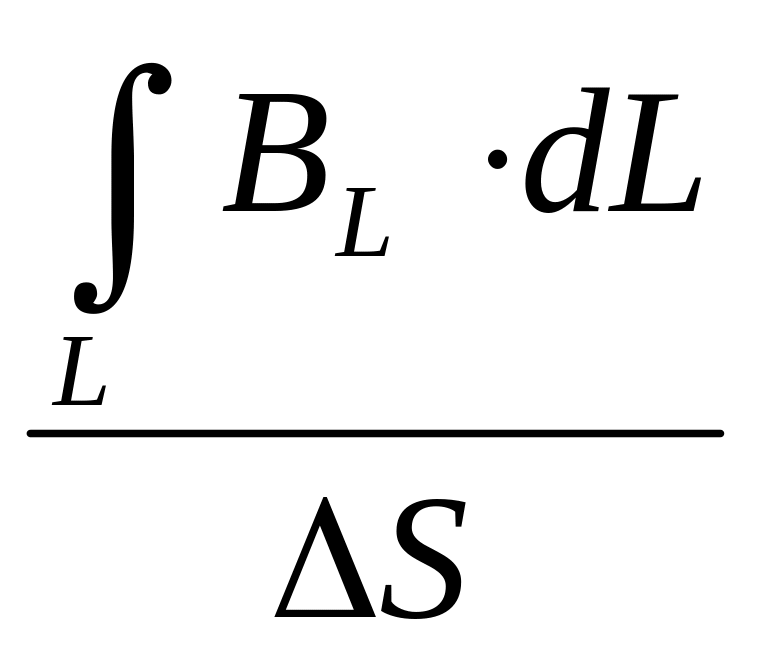= (rot В)_n

Дифференциальная форма теоремы о циркуляции вектора В в векторном виде записывается соотношением:

rot В = μ₀ ·j,

где j – плотность тока в данной точке. Таким образом, векторное поле, ротор которого равен нулю, является потенциальным (электростатическое поле), в противном случае – вихревым (магнитное поле).