После изучения главы необходимо знать следующее:

• Периодические процессы, протекающие в колебательном контуре.

• Собственные незатухающие колебания. Дифференциальное уравнение, его решение.

• Затухающие колебания. Дифференциальное уравнение, его решение.

• Вынужденные колебания. Дифференциальное уравнение, его решение.

• Переменный электрический ток.

• Ток смещения. Уравнения Максвелла.

• Электромагнитные волны. Их свойства и закономерности распространения.

4.1. Электрический колебательный контур

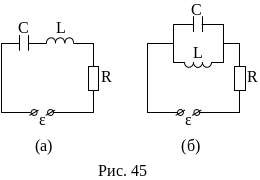
Колебательным контуром называется замкнутая электрическая цепь, в которой могут возбуждаться электромагнитные колебания (то есть происходит переход электрической энергии в магнитную и обратно), состоящая из последовательно (рис. 45, а) или параллельно (рис. 45, б) соединенных конденсатора с емкостью С и катушки с индуктивностью L, электрического активного сопротивления R и источника тока с периодически изменяющейся, например синусоидальной (гармонической), электродвижущей силой (ЭДС) Е = Е_msin(ωt), где Е_m – амплитуда ЭДС, ω – ее циклическая частота.

Процессы в колебательном контуре исследуются в области циклических частот ω << , где с – скорость света, L – характерные размеры системы, для которой выполняется условие квазистационарности, то есть токи и поля меняются не очень быстро и можно пренебречь запаздыванием процессов по времени.

Свободные незатухающие электромагнитные колебания. В идеализированном колебательном контуре, не обладающем активным сопротивлением (R = 0) и без источника тока Е, в условиях небольших частот колебаний (процесс квазистационарный) и «закрытости» контура (контур не является антенной и нет потерь энергии на излучение электромагнитных волн), происходят свободные незатухающие электромагнитные колебания, то есть энергия контура переходит из электрической в магнитную и обратно без потерь.

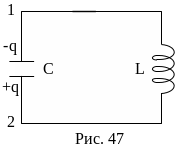
Колебания в контуре можно вызвать, либо зарядив конденсатор с емкостью С, сообщив обкладкам конденсатора начальные разноименные заряды (+q) и (–q), либо возбудив в катушке с индуктивностью L ток , например, путем выключения внешнего магнитного поля, пронизывающего витки катушки.

Полная энергия W контура, равна сумме энергий W_э = электрического поля, возникающего между обкладками заряженного конденсатора, и энергии W_м = магнитного поля, обусловленного током, текущим через индуктивность при, например, разрядке конденсатора, замкнутого на индуктивность, не расходуется на нагревание проводов и будет оставаться постоянной.

Из сопоставления электромагнитных колебаний в контуре и механических колебаний пружинного маятника (рис. 46) следует, что энергия электрического поля W_э аналогична потенциальной энергии упругой деформации , а энергия магнитного поля W_м аналогична кинетической энергии .

Индуктивность L играет роль массы m, величина, обратная емкости , роль жесткости пружины выполняет k, заряду q соответствует смещение маятника из положения равновесия x, а силе тока  = – скорость v = dx/dt. Аналогия распространяется и на описывающие эти колебания математические уравнения.

Условимся считать положительным ток, заряжающий конденсатор, тогда имеем:  = (при ином выборе  = - ) (рис. 47).

Закон Ома для участка цепи, содержащего индуктивность, при выбранном правиле знаков для обхода контура и для заряда конденсатора имеет вид:

∙R = (φ₁ – φ₂) + ε₁₂,

где R – сопротивление проводов и катушки (в случае свободных колебаний R равно нулю), (φ₁ – φ₂) = - , ε₁₂ = ε_с = - L – ЭДС самоиндукции, которая поддерживает наибольшее значение _m силы тока в витках катушки (W = W_м) при полной разрядке конденсатора (W_э = 0). С учетом данных соотношений в общем случае закон Ома принимает вид:

∙R = - - L ,

откуда получается уравнение:

+ + q = 0.

Если сопротивление контура пренебрежимо мало и можно считать R = 0 (что соответствует условию R << , уравнение принимаеи вид:

+ q = 0,

решением которого является функция q = q_m∙cos(ω₀t + φ₀), то есть заряд конденсатора изменяется по гармоническому закону с циклической частотой свободных незатухающих электромагнитных колебаний (собственной частотой контура) ω₀ = и периодом свободных незатухающих колебаний в контуре Т = = (формула Томсона).

Напряжение на конденсаторе отличается от заряда множителем (1/С):

U = cos(ω₀t + φ₀) = U_mcos(ω₀t + φ₀).

Сила тока опережает по фазе напряжение на конденсаторе на :

 = _mcos(ω₀t + φ₀ + ).

Энергия контура W = + в момент максимальной зарядки q_m конденсатора равна W = , а когда заряд конденсатора равен нулю, то W = . Для зависимости магнитной и электрической энергии от времени верны такие же соотношения, как для кинетической и потенциальной энергии при механических колебаниях.

Затухающие электромагнитные колебания. Если в колебательной системе происходят потери энергии, то амплитуда колебаний уменьшается со временем. Энергия, запасенная в реальном колебательном контуре, обладающем активным сопротивлением (R ≠ 0), постепенно расходуется в этом сопротивлении на его нагревание, вследствие чего свободные электромагнитные колебания затухают, если потери энергии на джоулево тепло не восстанавливаются. Введя обозначение β = , которое называется коэффициентом затухания, уравнению затухающих электромагнитных колебаний можно придать вид:

+ ∙ + ∙ q = + 2 β ∙ + ω₀²q = 0.

При условии затухания β² < ω₀², то есть при < , решение уравнения имеет вид:

q = q_m0∙exp(-βt)∙cos(ωt + φ₀),

где ω = = , q_m0 – амплитудное значение заряда при t = 0. Таким образом, частота затухающих колебаний ω меньше собственной частоты ω₀. При R = 0 частота ω становится равной ω₀. На рис. 48 изображен график функции q = q(t).

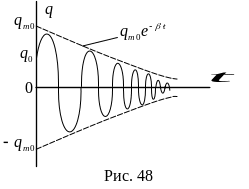
Графики для напряжения и силы тока имеют аналогичный вид. Логарифмический декремент затухания электромагнитных колебаний является характеристикой контура и обратен числу колебаний N, совершаемых за время, в течение которого амплитуда уменьшается в е раз:

λ = = β∙T = = .

Если затухание невелико, можно положить, что ω ≈ ω₀ = и тогда:

λ ≈ π∙R∙ = π∙R∙ .

Колебательный контур часто характеризуют его добротностью Q, которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания:

Q = = π∙N,

то есть добротность контура тем выше, чем большее число колебаний успеет совершиться прежде, чем амплитуда уменьшится в е раз. В случае слабого затухания

Q = ,

где – волновое сопротивление контура.

Вынужденные электромагнитные колебания. В реальном колебательном контуре (рис. 45), сопротивление R которого отлично от нуля, для получения незатухающих электромагнитных колебаний к контуру постоянно подводится энергия источника тока Е, которая восстанавливает потери на джоулево тепло. Электромагнитные колебания, возникающие в контуре под действием непрерывной электродвижущей силы Е(t) источника тока, называются вынужденными колебаниями и описываются дифференциальным уравнение, как и для механической колебательной системы:

+ 2β + ω₀²q = ,

Где q – заряд на конденсаторе, β = – коэффициент затухания, а величина ω₀ = – циклическая частота собственных колебаний контура. Рассмотрим установившиеся колебания под действием гармонического воздействия Е(t) = Е_msin(ωt). Колебания заряда происходят по закону q = q_mcos(ωt + φ), где амплитуда q_m и сдвиг по фазе φ определяются по формулам:

q_m = = ,

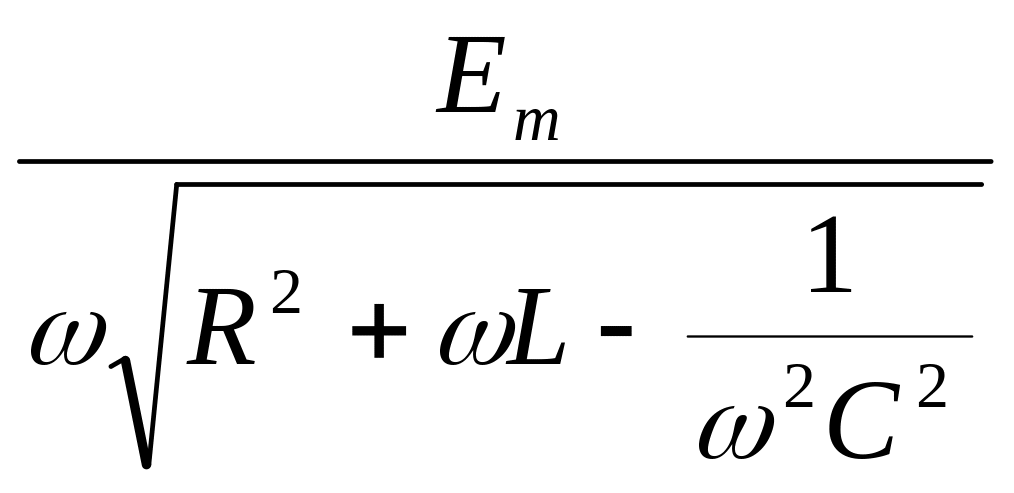tgφ = = .

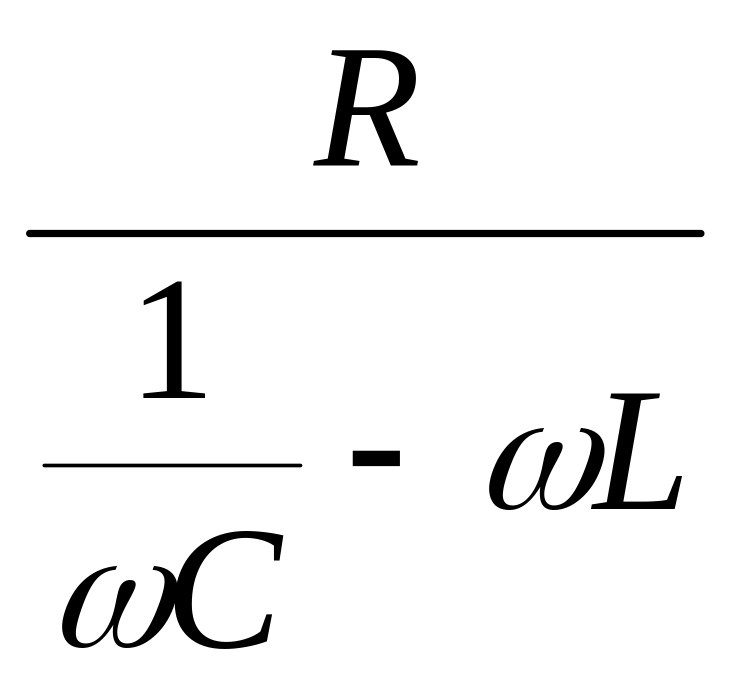Однако в электрической цепи интерес представляют не колебания заряда, а колебания тока  = , которые также происходят по гармоническому закону  = _mcos(ωt - φ₁), с амплитудой и сдвигом по фазе, равными соответственно:

_m = ω∙q_m = ,

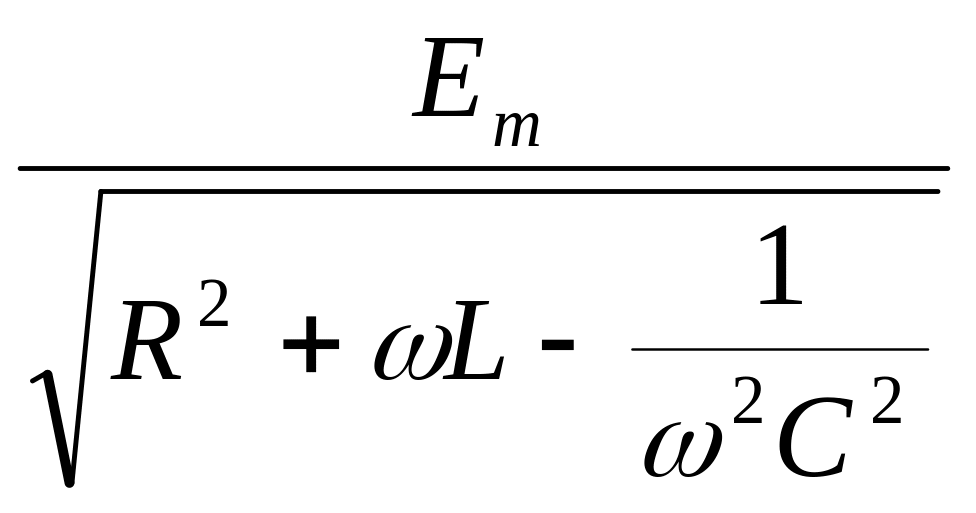tgφ₁ = .

Максимум амплитуды колебаний тока (резонанс) достигается при частоте ω_р = ω₀ = , а его значение на резонансной частоте ω_р равно _m = . Таким образом, при резонансе колебания тока происходят в фазе с колебаниями ЭДС.

Вынужденные электромагнитные колебания можно осуществить также, если вместо переменной ЭДС подать на образовавшиеся контакты разорванного контура переменное напряжение U = U_mcos(ωt), которое прибавляется к ЭДС самоиндукции. Тогда уравнение вынужденных электромагнитных колебаний в контуре примет вид:

∙R = (φ₁ – φ₂) + (ε_с + U) = - - L ∙ + U,

откуда получается выражение:

∙R + + L ∙ = U_R + U_C + U_L = U = U_mcos(ωt),

где колебания напряжения на сопротивлении U_R, конденсаторе U_C и катушке индуктивности U_L описываются следующими формулами:

U_R = ∙R = _m∙R∙cos(ωt - φ₁) = U_Rmcos(ωt - φ₁),

U_C = = _m∙ ∙cos(ωt - φ₁ – ) = U_Cmcos(ωt - φ₁ – ),

U_L = L∙ = _m∙ω∙L∙cos(ωt - φ₁ + ) = U_Lmcos(ωt - φ₁ + ).

Получается, что сумма напряжений на отдельных элементах контура равна в каждый момент времени напряжению U, приложенному извне.

Коэффициенты пропорциональности между амплитудами тока и напряжения называют: X_C = - емкостным сопротивлением, X_L = ω∙L - индуктивным сопротивлением. Величину X = X_L - X_C называют реактивным сопротивлением цепи, сопротивление R – активным сопротивлением в том смысле, что только на нем рассеивается энергия, величину Z = – полным сопротивлением. Можно написать, что _m = , а tgφ₁ = . Все фазовые соотношения становятся наглядными при использовании векторных диаграмм (рис. 49), где U изображается вектором, равным сумме векторов U_R, U_C, U_L.

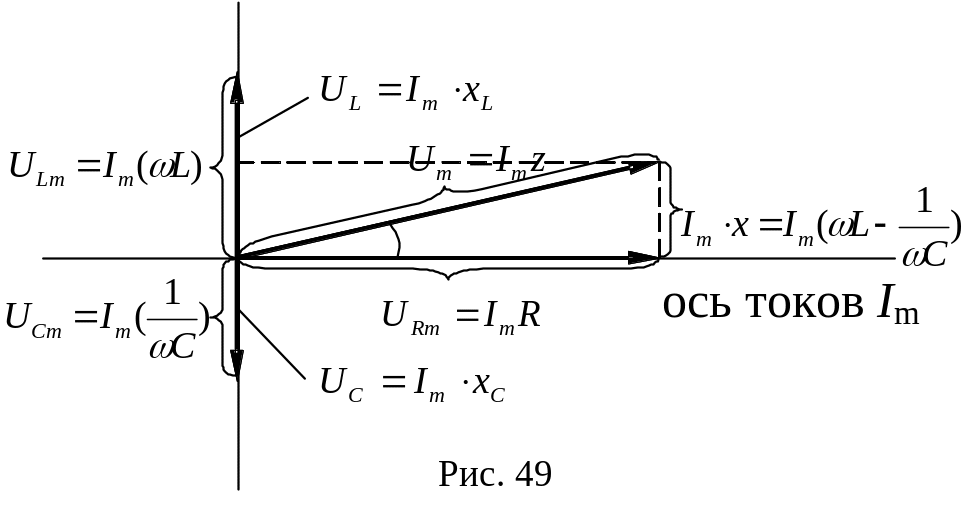
В последовательном колебательном контуре (рис. 45, а) на резонансной частоте при X_L = X_C противофазные колебания напряжений (резонанс напряжений) на емкости U_C и на индуктивности U_L компенсируют друг друга и сопротивление цепи превращается в активное сопротивление Z = R. Это соответствует минимальной величине полного сопротивления Z, поэтому на резонансной частоте электрический ток в такой цепи достигает своего максимального значения, что иллюстрирует амплитудно – частотная характеристика (АЧХ) последовательного колебательного контура (рис. 50).

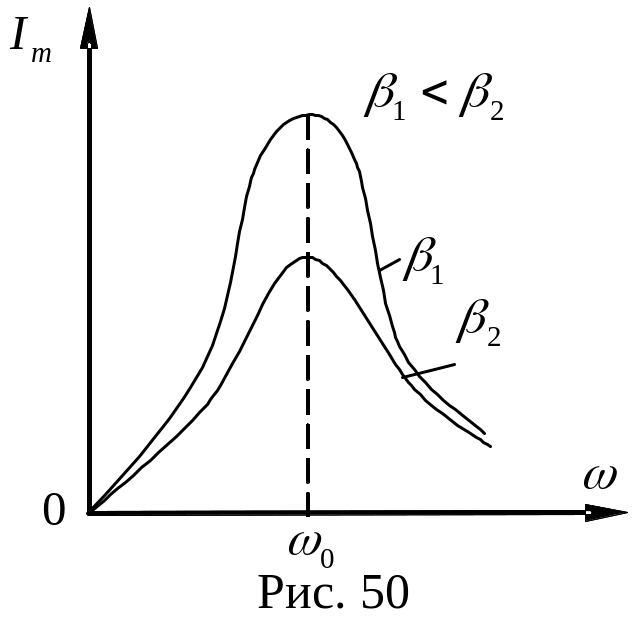
Максимум амплитуды _m колебаний тока при резонансе получается тем выше и острее, чем меньше коэффициент затухания β = , то есть чем меньше активное сопротивление R и больше индуктивность L контура.

В параллельном колебательном контуре (рис. 45, б) полное сопротивление Z цепи на резонансной частоте ω₀ достигает своего максимального значения (рис. 51), тем самым, подтверждая резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные индуктивное и емкостное сопротивления (резонанс токов). При этом падение напряжения в цепи достигает своего максимального значения.

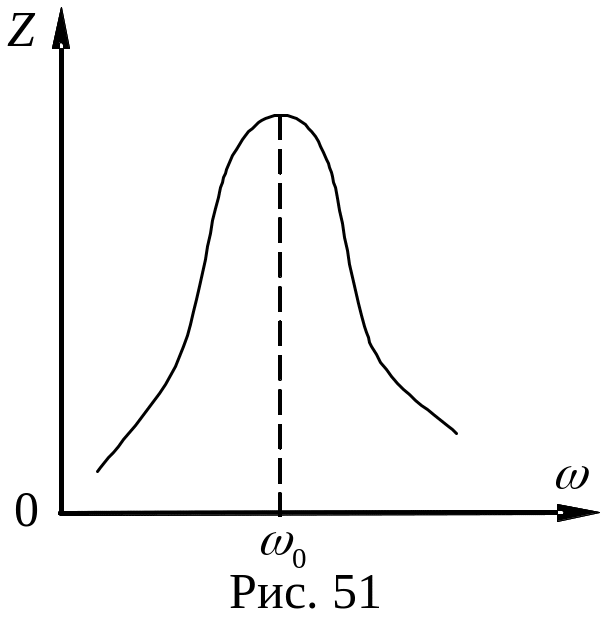
Заметим, что резонансная частота не зависит от сопротивления резистора R (активного сопротивления).