3.12. Энергия магнитного поля

Энергия магнитного поля электрического тока – собственная энергия тока  в контуре (электрической цепи) с индуктивностью L, численно равная работе внешних сил и источников, затрачиваемой на приодоление ЭДС самоиндукции при создании тока (или работе вихревого электрического поля при его уничтожении).

Предположим, что в неферромагнитной среде, так что L не зависит от , находится электрическая цепь с внешним источником ЭДС Е, катушкой индуктивности L, резистором R, ключом К (сопротивлением проводов пренебрегаем) (рис. 43). Полное сопротивление цепи равно R.

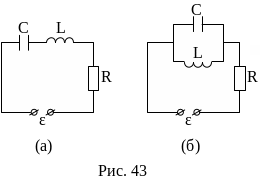
По правилу Ленца дополнительные токи, возникающие вследствие самоиндукции, всегда направлены так, чтобы противодействовать изменениям тока в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при размыкании цепи происходит не мгновенно, а постепенно.

Для данной электрической цепи можно рассмотреть три различных состояния.

а) Равновесное состояние, которое наступает через определенный промежуток времени t после замыкания ключа К (кривая 1, рис. 44).

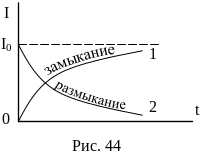
В цепи устанавливается постоянный ток  и постоянное магнитное поле в катушке L. При этом работа источника ЭДС Е идет на выделение ленц - джоулева тепла:

dA = dQ =  ·R·dt.

б) Неравновесное состояние в момент замыкания ключа. Процесс нарастания тока в цепи от 0 до  сопровождается увеличением тока в катушке индуктивности, что приводит к появлению изменяющегося (увеличивающегося) магнитного поля. Создаваемая этим током магнитная индукция В (и собственный магнитный поток Ф_с) будет меняться со скоростью, пропорциональной d/dt. Следовательно, возникающее в каждой точке пространства вихревое электрическое поле тоже пропорционально скорости изменения тока d/dt. Это вихревое поле создает в контуре ЭДС самоиндукции

ε_с = - = - L ,

направленную против Е, и замедляющую нарастание тока в цепи. Таким образом, увеличение энергии магнитного поля равно отрицательной работе электрического тока:

dA = (-ε_с)··dt,

где 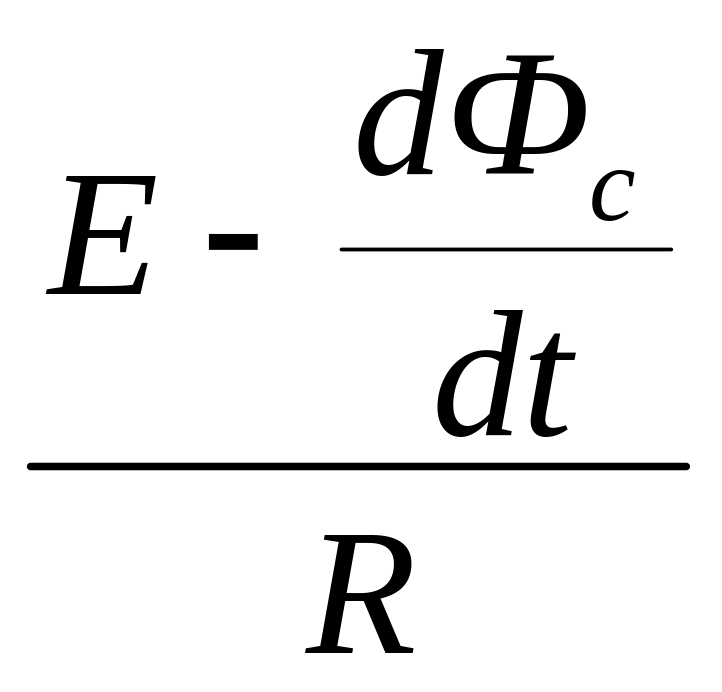 = =  ·[1 – exp(- )] – сила тока в цепи изменяется не мгновенно, а по экспоненциальному закону;  = . Энергия магнитного поля определяется интегрированием:

W = = = = L = .

в) Неравновесное состояние в момент размыкания ключа (кривая 2, рис. 44). Процесс убывания тока в цепи от  до 0 сопровождается уменьшением тока в катушке индуктивности, что приводит к появлению изменяющегося (уменьшающегося) магнитного поля. Создаваемая этим током магнитная индукция В (и собственный магнитный поток Ф_с) будет меняться со скоростью, пропорциональной d/dt. Следовательно, возникающее в каждой точке пространства вихревое электрическое поле тоже пропорционально скорости изменения тока d/dt. Это вихревое поле создает в контуре ЭДС самоиндукции

ε_с = - = - L ,

направленную по Е, и замедляющую процесс спада тока в цепи. При размыкании цепи ток уменьшается не мгновенно, а по экспоненциальному закону:

 =  ·exp(- ).

Таким образом, уменьшение энергии магнитного поля равно положительной работе электрического тока, идущей на выделение ленц – джоулева тепла:

W = = - L = .

Из вышесказанного следует, что выражение для энергии магнитного поля (собственную энергию катушки индуктивности) можно уподобить выражению для кинетической энергии в механике . Получается, что индуктивность L можно рассматривать как меру «инертности» контура по отношению к изменению в нем электрического тока, то есть для магнитного поля индуктивность L подобна массе тела m.

Такую же аналогию можно провести и для энергии электрического поля (собственной энергии плоского конденсатора емкостью С, заряд обкладок которого равен q) , которая подобна потенциальной энергии . Для электрического поля величина подобна упругости пружины k.

Плотность энергии магнитного поля. Энергию магнитного поля в любом объеме V неферромагнитной среды можно определить по формуле:

W = ,

если известна величина = , называемая плотностью энергии магнитного поля. Если в качестве магнитного поля рассматривать однородное магнитное поле соленоида достаточно большой длины l с сечением S, то выражение для плотности энергии принимает вид:

= = = ,

где H = - напряженность магнитного поля соленоида; n – количество витков на единицу длины l соленоида; V = S∙l – объем соленоида; L = - индуктивность соленоида; B - индукция магнитного поля соленоида.

4 ГЛАВА
	ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
		4.1. ЭЛЕКТРИЧЕСКИЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР
		4.2. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
		4.3. ТОК СМЕЩЕНИЯ. УРАВНЕНИЯ МАКСВЕЛЛА
		4.4. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Среди различных электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей.

Электромагнитные колебания рассмотрены на примере колебательного контура: собственные незатухающие колебания (в отсутствии активного сопротивления), затухающие колебания (при наличии активного сопротивления) и вынужденные (при наличии внешней периодически изменяющейся ЭДС). Частным случаем вынужденных колебаний является переменный электрический ток.

Электрическое и магнитное поля являются проявлением единого электромагнитного поля, теория которого была разработана Максвеллом. Эта теория позволила не только объяснить уже известные факты, но и предсказать ряд новых явлений, и в первую очередь, существование электромагнитных волн, описать их свойства.

Цель главы – изучить процессы, протекающие в колебательном контуре в зависимости от наличия в цепи активного сопротивления и периодически изменяющейся внешней ЭДС а также в цепях переменного электрического тока, изучить основы теории Максвелла для электромагнитного поля, свойства электромагнитных волн и особенности их распространения.