2.4. Закон Джоуля - Ленца
Электрический ток, протекающий в цепи, может совершать тепловое, магнитное и химическое действия.
Закон Джоуля – Ленца в интегральной форме. Предположим, что силы электростатического поля совершают работу dA, перемещая заряд dq через поперечное сечение изотропного проводника за время dt, которая затрачивается на нагревание проводника с выделением количества теплоты
dQ = dA = U∙dq = U∙∙dt = 2∙R∙dt,
где U – падение напряжения на проводнике, - сила тока в проводнике, R – сопротивление проводника.
Если сила тока изменяется со временем (t), то количество теплоты, выделяющееся за время t во всем проводнике, вычисляется по формуле:
Q
=
2∙R∙dt.
Для участка цепи постоянного тока ( = const) количество теплоты, выделившейся во всем проводнике, равно Q = 2∙R∙t.
Закон Джоуля – Ленца в дифференциальной форме. Выделим в проводнике элементарный объем dV в виде цилиндра (см. рис. 20) и перейдем к выражению, характеризующему выделение теплоты в различных местах проводника. Согласно закону Джоуля – Ленца за время dt в этом объеме выделится теплота
dQ
= 2∙R∙dt
= ρ∙
∙(j∙dS)2∙dt,
где dS – сечение цилиндра, dL – длина цилиндра, R = ρ∙dL/dS – сопротивление цилиндра, j – плотность тока в данном месте проводника, сила тока в цилиндре равна = j∙dS.
Разделив выражение для dQ на dV и dt, найдем количество теплоты, выделяющееся в единице объема в единицу времени, то есть удельную тепловую мощность тока
wтепл
=
= ρ∙j2
= σ∙E2
=
.
В векторном виде закон Джоуля – Ленца в дифференциальной форме записывается как wтепл = j∙E. Полученные формулы справедливы и для неоднородного участка при условии, что действующие в нем сторонние силы имеют нехимическое происхождение.
2.5. Расчет разветвленной цепи. Законы Кирхгофа
Законы Кирхгофа позволяют рассчитывать сложные электрические цепи, то есть определять силу и направление постоянного или квазистационарного тока в любой части разветвленной (многоконтурной) системы проводников, если известны сопротивления Ri и ЭДС εi всех его участков.
Первый закон (правило) Кирхгофа вытекает из закона сохранения заряда и состоит в том, что алгебраическая сумма токов i, сходящихся в точке разветвления проводников – узле, равна нулю:
∑i = 0;
Узел это точка соединения не менее чем трех проводников,
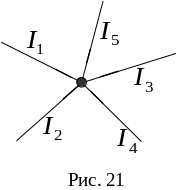
Токи, притекающие к узлу, считаются положительными, вытекающие из него – отрицательными. Например, исходя из уравнения непрерывности для узла, изображенном на рис.21, через который протекают постоянные токи, имеем:
j∙ds
=
= 0 =>
1
+ 2
- 3
+ 4
- 5
= 0.
Второй закон (правило) Кирхгофа: в любом замкнутом контуре, выделенном в сложной цепи проводников, алгебраическая сумма падений напряжений i∙Ri на отдельных участках контура (Ri – сопротивление i – го участка) равна алгебраической сумме ЭДС εi в этом контуре:
∑(i∙Ri) = ∑ εi.
При этом следует произвольно выбрать положительное направление токов и ЭДС. Например, следует считать их положительными, если направление токов совпадает с направлением обхода контура по часовой стрелке, а ЭДС повышает потенциал в направлении этого обхода, отрицательными – при противоположном направлении. Второй закон Кирхгофа получается в результате применения закона Ома к различным участкам замкнутой цепи.
Для сложной многоконтурной электрической цепи из n проводников, образующих m узлов, составляют n уравнений:
- (m - 1) уравнение для узлов на основе первого закона Кирхгофа;
- (n - m + 1) уравнений для независимых замкнутых контуров на основе второго закона Кирхгофа. Решение этой системы уравнений и дает значения искомых токов. Если при решении для какого-либо тока получается отрицательное значение, то это означает, что его направление противоположно выбранному.