1.9. Электроемкость проводников

Рассмотрим уединенный проводник — проводник, удаленный от других тел и зарядов. Из опыта следует, что разные проводники, будучи одинаково заряженными, имеют разные потенциалы.

Физическая величина С, равная отношению заряда проводника q к его потенциалу φ, называется электрической емкостью этого проводника.

Электроемкость уединенного проводника численно равна заряду, который нужно сообщить этому проводнику для того, чтобы изменить его потенциал на единицу.

Она зависит от формы и размеров проводника и от диэлектрических свойств окружающей среды. Емкости геометрически подобных проводников пропорциональны их линейным размерам.

В СИ единицей электроемкости является фарад (Ф) – это емкость проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1Кл. На практике используются дольные единицы: 1мкФ = 10^-6 Ф; 1нФ = 10^-9 Ф; 1пф = 10^-12 Ф.

В качестве примера, рассчитаем электроемкость С уединенного проводника в форме шара радиуса R, который равномерно заряжается с объемной плотностью ρ при сообщении ему заряда q.

С помощью теоремы Остроградского – Гаусса можно найти, что напряженность поля проводящего шара равна:

Е = , а потенциал равен: φ = ,

где ρ = 3q/4πR³. После подстановки получаем С = 4πε₀εR.

Взаимная электроемкость двух проводников – величина С, численно равная заряду q, который нужно перенести с одного проводника на другой для того, чтобы изменить разность потенциалов между ними φ₁ – φ₂ на единицу:

С = .

Взаимная емкость зависит от формы, размеров и взаимного расположения проводников, а также от относительной диэлектрической проницаемости среды, в которой они находятся.

Конденсатор – система двух разноименно заряженных равными по абсолютной величине зарядами проводников (обкладок), имеющих такую форму и расположение друг относительно друга, что поле, создаваемое такой системой, сосредоточено (локализовано) в ограниченной области пространства между его обкладками. Все силовые линии начинаются на положительной обкладке и заканчиваются на отрицательной. Все пространство, в котором сосредоточено поле, заполнено однородным диэлектриком. Конденсатор является прибором для накопления электрических зарядов и электрической энергии. По форме обкладок выделяют плоские, цилиндрические, сферические конденсаторы. Электроемкость конденсатора является взаимной емкостью его обкладок

С = = ,

где U – напряжение между обкладками (напряжение на конденсаторе).

Рассчитаем емкость плоского конденсатора С, у которого площадь обкладок S, заряд обкладок q, расстояние между обкладками d, относительная диэлектрическая проницаемость среды между обкладками ε.

По теореме Остроградского – Гаусса напряженность поля двух параллельных разноименно заряженных с поверхностной плотностью σ = q/S бесконечных плоскостей равна:

Е = .

При расстоянии d намного меньшем линейных размеров обкладок их можно считать бесконечными поверхностями. Учитывая, что Е = - grad φ приходим к соотношению Е∙d = U, откуда подстановкой получается, что напряжение на конденсаторе равно

U = ,

откуда емкость плоского конденсатора определяется выражением:

С = .

Для всех типов конденсаторов существует пробивное напряжение – разность потенциалов между обкладками, при которой происходит электрический разряд через слой диэлектрика. Пробивное напряжение зависит от толщины диэлектрика, его свойств и формы обкладок.

Соединение конденсаторов. Для получения необходимой емкости используют составные конденсаторы, которые получают соединением обкладок простых конденсаторов. Емкость составного конденсатора определяется по такой же формуле, что и для простого конденсатора и выражается через емкости его компонентов.

Параллельное соединение. Для увеличения емкости применяется параллельное соединение конденсаторов одноименно заряженными обкладками (рис. 12). Соединенные между собой обкладки образуют обкладки составного конденсатора.

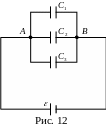
Суммарный заряд составного конденсатора q определяется из соотношения

q = q₁ + q₂ + q₃ = U_AB∙C₁ + U_AB∙C₂ + U_AB∙C₃ = U_AB (C₁ + C₂ + C₃) = U_AB∙C,

где U_AB = U₁ = U₂ = U₃ – напряжение, одинаковое на всех компонентах составного конденсатора, а С = C₁ + C₂ + C₃ – емкость составного конденсатора при параллельном соединении его компонентов (С = ∑С_i).

Последовательное соединение. Обкладками составного конденсатора служат обкладки крайних конденсаторов (рис. 13), полный заряд на каждой паре внутренних обкладок равен нулю.

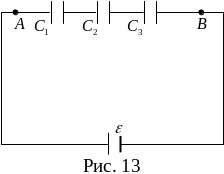
Получается, что заряд q всех компонентов составного конденсатора одинаковый, то есть q = q₁ = q₂ = q₃. Суммарное падение напряжения U_AB на составном конденсаторе равно сумме падений напряжений на каждом из его компонентов, то есть

U_AB = U₁ + U₂ + U₃ = + + = q ( + + ),

откуда следует, что емкость С составного конденсатора при последовательном соединении его компонентов может быть определена из соотношения:

= ∑ ,

то есть в нашем случае имеем:

= + + .