2.3. Деформации стержня и перемещения сечений. Условие жесткости
Под действием
растягивающих и сжимающих продольных
сил стержень длинной
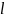соответственно удлиняется или
укорачивается на некоторую величину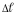
,
которая
называется
абсолютным
удлинением (абсолютной продольной
деформацией).
Отношение абсолютного удлинения к первоначальной длине стержня называется относительной продольной деформацией:
.
(2.6)
При растяжении деформации и ε являются положительными, а при сжатии – отрицательными.
Наряду с изменением длины стержня при растяжении и сжатии происходит изменение размеров его поперечного сечения. При сжатии стержня поперечные размеры его увеличиваются, а при растяжении уменьшаются. Это изменение характеризуют относительной поперечной деформацией '.
Экспериментально доказано, что при упругом деформировании стержня из изотропного материала относительная поперечная деформация ' постоянна для всех направлений в плоскости поперечного сечения и связана с относительной продольной деформацией ε линейной зависимостью
'
=
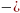
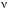ε.
Здесь – коэффициент Пуассона. Это механическая постоянная материала, определяемая экспериментально. Её величина для изотропных материалов колеблется в пределах
0 ≤ ≤ 0,5.
При упругом деформировании (когда напряжения не превышают предела пропорциональности материала) между нормальным напряжением и относительной продольной деформацией ε при растяжении (сжатии) существует линейная зависимость, называемая законом Гука:
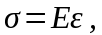(2.7)
где Е – модуль упругости первого рода или модуль Юнга. Это механическая постоянная материала, определяемая экспериментально.
В общем
случае абсолютное удлинение
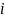–го
участка стержня определяется по формуле
|
(2.8) |
,
где
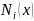– аналитическое выражение нормальной
силы на
-ом
участке стержня;
– длина этого участка;
– площадь поперечного сечения
-го
участка стержня;
– модуль упругости первого рода или
модуль Юнга для материала
-го
участка стержня.
Если
нормальная сила
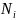постоянна (т.е.
)
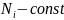по длине участка
,
то формула (2.8) преобразуется к виду:
|
(2.9) |
Произведение
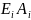называют жесткостью
-го
участка стержня при растяжении и сжатии,
а формулы (2.8) и (2.9)
развернутым
законом Гука при растяжении и сжатии.
Вследствие
изменения длины отдельных участков
нагруженного стержня его поперечные
сечения получают линейные перемещения
вдоль продольной оси стержня
.
Понятия деформации и перемещения нельзя отождествлять, так как перемещающаяся часть стержня может быть недеформированной.
Взаимное перемещение двух поперечных сечений численно равно изменению длины участка стержня, заключенного между этими сечениями.
Абсолютное
перемещение любого j-го
сечения стержня
при растяжении и сжатии определяется
как сумма абсолютных удлинений
участков стержня, заключенных между
рассматриваемым и неподвижным
(закрепленным) сечениями, т.е.
|
(2.10) |
где
–
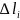абсолютное удлинение
- го участка стержня.
В некоторых случаях работоспособность конструкции определяется не только её прочностью, но и жесткостью, т.е. способностью воспринимать нагрузки без недопустимых упругих деформаций.
При расчетах на жесткость определяют перемещения сечений стержней или определенных точек (или узлов) конструкции, основными элементами которой являются стержни, и сопоставляют их с допускаемыми перемещениями, т.е. условие жесткости записывают в виде
|
(2.11) |
,
где
–значение перемещения сечения или
точки (узла) конструкции, взятое по
абсолютной величине;
– допускаемое значение перемещения
сечения или точки (узла) конструкции,
устанавливаемое из норм проектирования
или из конструктивных соображений.
Перемещение точки (узла) конструкции, основными элементами которой являются стержни, определяется по абсолютным удлинениям стержней , рассчитанным по формуле (2.8) (или (2.9)), с учетом геометрических особенностей этой конструкции.
Из условия жесткости (2.11) выполняют такие же виды расчетов, что и из условия прочности (2.3).
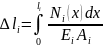