Вариант 14.8

А1. Отношение стороны треугольника к синусу противолежащего угла равно 4, тогда радиус окружности, описанной около этого треугольника, равен

1) 6 2) 1 3) 4 4) 2

А2. В треугольнике АВС проведены высоты AD и СМ. Если 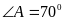, , 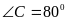то угол АМС ( в градусах ) равен

1) 120 2) 135 3) 170 4) 150

А3. В треугольнике АВС медиана АМ продолжена за точку М на расстояние MD=АМ. Если АС=2, то BD равно

1) 1 2) 2 3) 4 4) 2

А4. Периметр треугольника равен 8, тогда периметр треугольника, стороны которого параллельны сторонам данного треугольника и проходят через его вершины, равен

1) 16 2) 24 3) 32 4) 40

А5. Дан куб 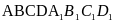с ребром, равным , тогда расстояние между прямыми 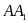и ВС равно

1) 2) 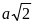3) 4)

В1. В параллелограмме ABCD биссектриса тупого угла ВМ делит противолежащую сторону на отрезки АМ=7, MD=14. Тогда периметр параллелограмма равен

В2. В прямоугольный треугольник АВС вписан квадрат так, что две его вершины лежат на гипотенузе АВ, а две другие − на катетах. Радиус круга, описанного около треугольника АВС, относится к стороне квадратов как 13:6. Тангенс большего из острых углов треугольника равен

В3. Вычислите площадь боковой поверхности правильной треугольной пирамиды, если радиус описанной около основания окружности равен √3, а высота пирамиды равна 1.

В4. Вычислите объем правильной треугольной пирамиды, сторона основания которой равна 6, а апофема равна √15.

В5. Через две образующие конуса, угол между которыми равен , проведена

плоскость, составляющая с основанием . Найти объем конуса, если его высота равна .

Вариант 14.9

А1. Сторона правильного треугольника равна , тогда его высота равна

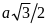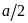1) 2) 3) 4)

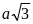
А2. В треугольнике АВС медиана BD перпендикулярна АС и равна ее половине. Тогда угол АВС ( в градусах ) равен

1) 90 2) 75 3) 60 4) 45

А3. Один из углов прямоугольного треугольника равен , а его гипотенуза равна 16. Тогда меньший из отрезков, на которые делит гипотенузу высота, проведенная из прямого угла, равен

1) 2 2) 3 3) 4 4) 6

А4. В треугольнике АВС . Биссектриса AD, медиана ВМ и высота СК пересекаются в точке О, тогда 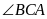( в градусах ) равен

1) 45 2) 60 3) 90 4) 120

А5. Диагональ единичного куба равна

1) 3 2) 3) 4)

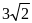
В1. Около круга описана трапеция, периметр которой равен 12, тогда средняя линия трапеции равна

В2. В прямоугольном треугольнике АВС с прямым углом А биссектриса угла В пересекает сторону АС в точке D. Если известно, что АВ-6, ВС=10, то площадь треугольника DBC равна

В3. Найдите площадь боковой поверхности правильной че­тырехугольной пирамиды, если высота равна 2, а пло­ские углы при вершине прямые.

В4. Вычислите объем правильной треугольной пирамиды, высота которой равна 3√3, а радиус окружности, впи­санной в основание, равен 2.

В5. Найти угол между образующей и основанием усеченного конуса, полная поверхность которого вдвое больше поверхности вписанного в него шара.