
- •Тематические тесты по математике
- •М.Ю. Глазкова, в.Н. Колпачев, т.Г. Святская, в.А. Попова, е.И.Ханкин
- •1. Степени с рациональными показателями. Корни. Вариант 1.1.
- •Вариант 1.2.
- •Вариант 1.3.
- •Вариант 1.4.
- •Вариант 1.5.
- •Вариант 1.6.
- •Вариант 1.7.
- •Вариант 1.8.
- •Вариант 1.9.
- •Вариант 1.10.
- •2. Рациональные уравнения Вариант 2.1.
- •Вариант 2.2.
- •Вариант 2.3.
- •Вариант 2.4.
- •Вариант 2.5.
- •Вариант 2.6.
- •Вариант 2.7.
- •Вариант 2.8.
- •Вариант 2.9.
- •Вариант 2.10.
- •3. Уравнения, содержащие неизвестное под знаком модуля. Вариант 3.1
- •Вариант 3.2
- •Вариант 3.3
- •Вариант 3.4
- •Вариант 3.5
- •Вариант 3.6
- •Вариант 3.7
- •Вариант 3.8
- •Вариант 3.9
- •Вариант 3.10
- •4. Иррациональные уравнения Вариант 4.1
- •Вариант 4.2
- •Вариант 4.3
- •Вариант 4.4
- •Вариант 4.5
- •Вариант 4.6
- •Вариант 4.7
- •Вариант 4.8
- •Вариант 4.9
- •Вариант 4.10
- •5. Неравенства, содержащие неизвестные под знаком модуля. Иррациональные неравенства. Вариант 5.1.
- •Вариант 5.2.
- •Вариант 5.3.
- •Вариант 5.4.
- •Вариант 5.5.
- •Вариант 5.6.
- •Вариант 5.7.
- •Вариант 5.8.
- •Вариант 5.9.
- •Вариант 5.10.
- •6. Системы алгебраических уравнений. Рациональные неравенства Вариант 6.1
- •Вариант 6.2
- •Вариант 6.3
- •Вариант 6.4
- •Вариант 6.5
- •Вариант 6.6
- •Вариант 6.7
- •Вариант 6.8
- •Вариант 6.9
- •Вариант 6.10
- •7. Преобразование тригонометрических выражений. Вариант 7.1
- •Вариант 7.2
- •Вариант 7.3
- •Вариант 7.4
- •Вариант 7.5
- •Вариант 7.6
- •Вариант 7.7
- •Вариант 7.8
- •Вариант 7.9
- •Вариант 7.10
- •8. Тригонометрические уравнения Вариант 8.1
- •Вариант 8.2
- •Вариант 8.3
- •Вариант № 8.4
- •Вариант № 8.5
- •Вариант № 8.6
- •Вариант № 8.7
- •Вариант № 8.8
- •Вариант № 8.9
- •Вариант № 8.10
- •9. Показательные уравнения. Показательные неравенства. Вариант 9.1.
- •Вариант 9.2.
- •Вариант 9.3.
- •Вариант 9.4.
- •Вариант 9.5.
- •Вариант 9.6.
- •Вариант 9.7.
- •Вариант 9.8.
- •Вариант 9.9.
- •Вариант 9.10.
- •10. Логарифмические уравнения и неравенства Вариант № 10.1
- •Вариант № 10.2
- •Вариант №10.3
- •Вариант №10.4
- •Вариант №10.5
- •Вариант №10.6
- •Вариант № 10.7
- •Вариант 10.8
- •Вариант 10.9
- •Вариант 10.10
- •11. Логарифмические неравенства и системы показательных и логарифмических уравнений и неравенств. Вариант 11.1
- •Вариант 11.2
- •Вариант 11.3
- •Вариант 11.4
- •Вариант 11.5
- •Вариант 11.6
- •Вариант 11.7
- •Вариант 11.8
- •Вариант 11.9
- •Вариант 11.10
- •12. Текстовые задачи Вариант 12.1
- •Вариант 12.2
- •Вариант 12.3
- •Вариант 12.4
- •Вариант 12.5
- •Вариант 12.6
- •Вариант 12.7
- •Вариант 12.8
- •Вариант 12.9
- •Вариант 12.10
- •13. Начала анализа Вариант 13 .1
- •Вариант 13 .2
- •Вариант 13.3
- •Вариант 13 .4
- •Вариант 13 .5
- •Вариант 13 .6
- •Вариант 13.7
- •Вариант 13 .8
- •Вариант 13 .9
- •Вариант 13 .10
- •14. Геометрия Вариант 14.1
- •Вариант 14.2
- •Вариант 14.3
- •Вариант 14.4
- •Вариант 14.5
- •Вариант 14.6
- •Вариант 14.7
- •Вариант 14.8
- •Вариант 14.9
- •Вариант 14.10
- •15. Задачи с параметрами Вариант 15.1
- •Вариант 15 .2
- •Вариант 15.3
- •Вариант 15.4
- •Вариант 15.5
- •Вариант `15.6
- •Вариант 15.7
- •Вариант 15.8
- •Вариант 15.9
- •Вариант 15.10
- •Литература
- •Тематические тесты по математике
- •394006 Воронеж, ул. 20-летия Октября, 84
Вариант 14.6
А1.
Длина окружности, вписанной в квадрат,
равна
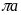 ,
тогда площадь квадрата равна
,
тогда площадь квадрата равна
1)
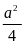 2)
2)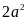 3)
3)
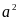 4)
4)
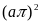
А2. Биссектрисы двух углов треугольника пересекаются под углом , тогда
Третий угол треугольника ( в градусах ) равен
1) 30 2) 45 3) 50 4) 40
А3. В прямоугольном треугольнике АВС на гипотенузе АВ взяты точки К и М, причем АК=АС, а ВМ=ВС, тогда угол МСК ( в градусах ) равен
1) 30 2) 60 3) 90 4) 45
А4. Периметр треугольника равен 14, тогда периметр фигуры, получившейся в результате соединения середин сторон исходного треугольника, равен
1) 5 2) 7 3) 9 4) 11
А5.
Объем правильной шестиугольной пирамиды
со стороной основания, равной а,
и боковым ребром, равным
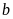 ,
равен
,
равен
1)
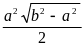 2)
2)
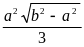 3)
3)
 4)
4)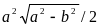
В1. Диагонали четырехугольника равны 2 и 6. Периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника, равен
В2. В прямоугольном треугольнике АВС с равными катетами АС и ВС на стороне АС, как на диаметре, построена окружность, пересекающая сторону АВ в точке М. Если ВМ= , то квадрат расстояния от вершины В до центра этой окружности равен
В3. Вычислите объем правильной треугольной пирамиды, если радиус описанной вокруг основания окружности равен √3 , а высота пирамиды равна 4√3.
В4. Вычислите объем правильной треугольной пирамиды, если радиус вписанной в основание окружности равен √З, а боковые ребра пирамиды равны 6.
В5. Треугольник со сторонами 10, 17, и 21 см вращается вокруг большей стороны. Вычислить объем полученной фигуры вращения.
Вариант 14.7
А1.
Радиус окружности, вписанной в правильный
треугольник, равен

 ,
тогда сторона треугольника равна
,
тогда сторона треугольника равна
1)
2)
3)
4)
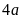
А2.
в равнобедренном треугольнике АВС
АС=20,
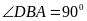 ,
тогда расстояние от вершины В до Ас
равно
,
тогда расстояние от вершины В до Ас
равно
1) 8 2) 7 3) 10 4) 9
А3. Медиана АМ треугольника АВС перпендикулярна его биссектрисе ВК. Если ВС=14, то АВ равно
1) 7 2) 11 3) 9 4) 5
А4.
Если один из углов параллелограмма на
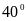 больше другого, то тупой угол параллелограмма
( в градусах ) равен
больше другого, то тупой угол параллелограмма
( в градусах ) равен
1) 75 2) 100 3) 110 4) 50
А5. Объем правильной четырехугольной пирамиды со стороной основания, равной , и углом боковой грани с плоскостью основания , равным , равен
1)
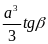 2)
2)
 3)
3)
 4)
4)
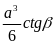
В1.
В треугольнике АВС сторона АВ=2,
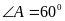 ,
,
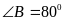 .
На стороне АС взята точка D,
так что AD=2,
тогда
.
На стороне АС взята точка D,
так что AD=2,
тогда
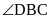 ( в градусах ) равен
( в градусах ) равен
В2. Средняя линия равнобедренной трапеции равна 10. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит ее на две части, отношение площадей которых равно 7:13, тогда высота трапеции равна
В3. Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если ее ребра равны 5, а радиус окружности, описанной вокруг основания равен 3√2.
В4. Вычислите объем правильной шестиугольной пирамиды, если сторона основания равна 4, а боковые ребра пирамиды равны 5.
В5. Около шара описан усеченный конус, площадь одного основания которого в 4 раза больше другого основания. Найти угол между образующей усеченного конуса и плоскостью основания.
