
- •Тематические тесты по математике
- •М.Ю. Глазкова, в.Н. Колпачев, т.Г. Святская, в.А. Попова, е.И.Ханкин
- •1. Степени с рациональными показателями. Корни. Вариант 1.1.
- •Вариант 1.2.
- •Вариант 1.3.
- •Вариант 1.4.
- •Вариант 1.5.
- •Вариант 1.6.
- •Вариант 1.7.
- •Вариант 1.8.
- •Вариант 1.9.
- •Вариант 1.10.
- •2. Рациональные уравнения Вариант 2.1.
- •Вариант 2.2.
- •Вариант 2.3.
- •Вариант 2.4.
- •Вариант 2.5.
- •Вариант 2.6.
- •Вариант 2.7.
- •Вариант 2.8.
- •Вариант 2.9.
- •Вариант 2.10.
- •3. Уравнения, содержащие неизвестное под знаком модуля. Вариант 3.1
- •Вариант 3.2
- •Вариант 3.3
- •Вариант 3.4
- •Вариант 3.5
- •Вариант 3.6
- •Вариант 3.7
- •Вариант 3.8
- •Вариант 3.9
- •Вариант 3.10
- •4. Иррациональные уравнения Вариант 4.1
- •Вариант 4.2
- •Вариант 4.3
- •Вариант 4.4
- •Вариант 4.5
- •Вариант 4.6
- •Вариант 4.7
- •Вариант 4.8
- •Вариант 4.9
- •Вариант 4.10
- •5. Неравенства, содержащие неизвестные под знаком модуля. Иррациональные неравенства. Вариант 5.1.
- •Вариант 5.2.
- •Вариант 5.3.
- •Вариант 5.4.
- •Вариант 5.5.
- •Вариант 5.6.
- •Вариант 5.7.
- •Вариант 5.8.
- •Вариант 5.9.
- •Вариант 5.10.
- •6. Системы алгебраических уравнений. Рациональные неравенства Вариант 6.1
- •Вариант 6.2
- •Вариант 6.3
- •Вариант 6.4
- •Вариант 6.5
- •Вариант 6.6
- •Вариант 6.7
- •Вариант 6.8
- •Вариант 6.9
- •Вариант 6.10
- •7. Преобразование тригонометрических выражений. Вариант 7.1
- •Вариант 7.2
- •Вариант 7.3
- •Вариант 7.4
- •Вариант 7.5
- •Вариант 7.6
- •Вариант 7.7
- •Вариант 7.8
- •Вариант 7.9
- •Вариант 7.10
- •8. Тригонометрические уравнения Вариант 8.1
- •Вариант 8.2
- •Вариант 8.3
- •Вариант № 8.4
- •Вариант № 8.5
- •Вариант № 8.6
- •Вариант № 8.7
- •Вариант № 8.8
- •Вариант № 8.9
- •Вариант № 8.10
- •9. Показательные уравнения. Показательные неравенства. Вариант 9.1.
- •Вариант 9.2.
- •Вариант 9.3.
- •Вариант 9.4.
- •Вариант 9.5.
- •Вариант 9.6.
- •Вариант 9.7.
- •Вариант 9.8.
- •Вариант 9.9.
- •Вариант 9.10.
- •10. Логарифмические уравнения и неравенства Вариант № 10.1
- •Вариант № 10.2
- •Вариант №10.3
- •Вариант №10.4
- •Вариант №10.5
- •Вариант №10.6
- •Вариант № 10.7
- •Вариант 10.8
- •Вариант 10.9
- •Вариант 10.10
- •11. Логарифмические неравенства и системы показательных и логарифмических уравнений и неравенств. Вариант 11.1
- •Вариант 11.2
- •Вариант 11.3
- •Вариант 11.4
- •Вариант 11.5
- •Вариант 11.6
- •Вариант 11.7
- •Вариант 11.8
- •Вариант 11.9
- •Вариант 11.10
- •12. Текстовые задачи Вариант 12.1
- •Вариант 12.2
- •Вариант 12.3
- •Вариант 12.4
- •Вариант 12.5
- •Вариант 12.6
- •Вариант 12.7
- •Вариант 12.8
- •Вариант 12.9
- •Вариант 12.10
- •13. Начала анализа Вариант 13 .1
- •Вариант 13 .2
- •Вариант 13.3
- •Вариант 13 .4
- •Вариант 13 .5
- •Вариант 13 .6
- •Вариант 13.7
- •Вариант 13 .8
- •Вариант 13 .9
- •Вариант 13 .10
- •14. Геометрия Вариант 14.1
- •Вариант 14.2
- •Вариант 14.3
- •Вариант 14.4
- •Вариант 14.5
- •Вариант 14.6
- •Вариант 14.7
- •Вариант 14.8
- •Вариант 14.9
- •Вариант 14.10
- •15. Задачи с параметрами Вариант 15.1
- •Вариант 15 .2
- •Вариант 15.3
- •Вариант 15.4
- •Вариант 15.5
- •Вариант `15.6
- •Вариант 15.7
- •Вариант 15.8
- •Вариант 15.9
- •Вариант 15.10
- •Литература
- •Тематические тесты по математике
- •394006 Воронеж, ул. 20-летия Октября, 84
Вариант 14.4
А1.
В прямоугольном треугольнике гипотенуза
равна
 а один из катетов −
а один из катетов −
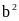 ,
тогда радиус описанной окружности равен
,
тогда радиус описанной окружности равен
1)
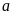 2)
2)
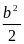 3)
4)
3)
4)
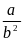
А2. Углы
треугольника относятся как 2:3:4, а внешние
углы треугольника относятся как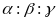 соответственно, тогда число
соответственно, тогда число
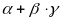 равно
равно
1) 14 2) 47 3) 17 4) 53
А3. Прямая АВ пересекает две другие параллельные прямые в точках А и В соответственно. Биссектриса ВС пересекает одну из параллельных прямых в точке С. Если АВ=5, то длина АС равна
1) 5 2) 2 3) 8 4) 22
А4. В
прямоугольном треугольнике АВС из
вершины прямого угла А опущена высота
АН на гипотенузу ВС. Если СН=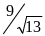 ,
а ВН=
,
а ВН=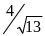 ,
то площадь треугольника АВС равна
,
то площадь треугольника АВС равна
1) 3 2) 7 3) 11 4) 12
А5. Высота прямоугольного треугольника АВС, опущенная на гипотенузу, равна 9,6. Из вершины прямого угла С восстановлен перпендикуляр СМ к плоскости треугольника АВС, причем См=28, тогда расстояние от точки М до гипотенузы АВ равно
1) 29,6 2) 29,2 3) 29,1 4) 29,7
В1. К окружности, вписанной в квадрат со стороной, равной 7, проведена касательная, пересекающая две его стороны. Тогда периметр отсеченного треугольника равен
В2. Около трапеции ABCD с основанием AD и ВС описана окружность радиусом 5. Центр описанной окружности лежит на основании AD. Если
Основание ВС равно 6, тогда диагональ АС равна
В3. Прямой круговой цилиндр пересечен плоскостью так, что в сечении получился квадрат. Найдите площадь боковой поверхности цилиндра, если известно, что радиус основания равен 10 см, а расстояние от сечения до оси цилиндра 6 см.
В4. Прямой круговой конус пересечен плоскостью параллельной основанию на расстоянии 3 см от вершины. Найдите объем конуса, если известно, что радиус сечения равен 4 см, а образующая конуса равна 10 см.
В5. В основании прямого параллелепипеда лежит параллелограмм со сторонами 1 и 4 см и острым углом . Большая диагональ параллелепипеда
равна 5 см. Определить его объем.
Вариант 14.5
А1. Площадь
правильного треугольника равна
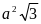 ,
тогда сторона треугольника равна
,
тогда сторона треугольника равна
1)
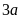 2)
3)
4)
2)
3)
4)

А2. Две параллельные прямые пересечены третьей, тогда угол ( в градусах ) между биссектрисами внутренних углов равен
1) 45 2) 90 3) 30 4) 60
А3. Один из углов прямоугольного треугольника равен , а его гипотенуза
Равна 8. Тогда больший из отрезков, на которые делит гипотенузу высота, проведенная из прямого угла, равен
1) 6 2) 12 3) 3 4) 4
А4.
Высота прямоугольного треугольника,
опущенная из вершины прямого угла, равна
1. Если один из острых углов треугольника
равен
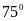 ,
то гипотенуза этого треугольника равна
,
то гипотенуза этого треугольника равна
1) 1 2) 3 3) 5 4) 4
А5.
Все боковые ребра пирамиды равны
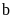 ,
а высота равна
,
а высота равна
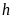 .
Тогда радиус описанной около основания
окружности равен
.
Тогда радиус описанной около основания
окружности равен
1)
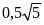 2)
3)
4)
2)
3)
4)
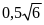
В1. Одна из сторон параллелограмма втрое больше другой. Если периметр параллелограмма равен 24, то сумма квадратов диагоналей равна
В2.
Наибольший угол прямоугольной трапеции
равен
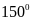 ,
а большая боковая сторона равна 10, тогда
разность большего и меньшего оснований
равна
,
а большая боковая сторона равна 10, тогда
разность большего и меньшего оснований
равна
В3. Тело ограничено двумя концентрическими шаровыми поверхностями. Удвоенное сечение плоскостью, проходящей через центр, равно 25 см2. Найдите площадь сечения, касательного к внутренней шаровой поверхности.
В4. В прямой круговой конус вписана сфера. Длина окружности, по которой сфера касается конуса, равна 3, расстояние от вершины конуса, до центра этой окружности равно 2/π, радиус основания конуса равен √3. Найдите боковую поверхность конуса.
В5.
Основание пирамиды служит ромб с острым
углом
.
Боковые грани наклонены к плоскости
основания под углом в
.
Определить полную поверхность пирамиды,
если радиус вписанного в ромб круга
равен
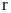 .
.
