
- •Тематические тесты по математике
- •М.Ю. Глазкова, в.Н. Колпачев, т.Г. Святская, в.А. Попова, е.И.Ханкин
- •1. Степени с рациональными показателями. Корни. Вариант 1.1.
- •Вариант 1.2.
- •Вариант 1.3.
- •Вариант 1.4.
- •Вариант 1.5.
- •Вариант 1.6.
- •Вариант 1.7.
- •Вариант 1.8.
- •Вариант 1.9.
- •Вариант 1.10.
- •2. Рациональные уравнения Вариант 2.1.
- •Вариант 2.2.
- •Вариант 2.3.
- •Вариант 2.4.
- •Вариант 2.5.
- •Вариант 2.6.
- •Вариант 2.7.
- •Вариант 2.8.
- •Вариант 2.9.
- •Вариант 2.10.
- •3. Уравнения, содержащие неизвестное под знаком модуля. Вариант 3.1
- •Вариант 3.2
- •Вариант 3.3
- •Вариант 3.4
- •Вариант 3.5
- •Вариант 3.6
- •Вариант 3.7
- •Вариант 3.8
- •Вариант 3.9
- •Вариант 3.10
- •4. Иррациональные уравнения Вариант 4.1
- •Вариант 4.2
- •Вариант 4.3
- •Вариант 4.4
- •Вариант 4.5
- •Вариант 4.6
- •Вариант 4.7
- •Вариант 4.8
- •Вариант 4.9
- •Вариант 4.10
- •5. Неравенства, содержащие неизвестные под знаком модуля. Иррациональные неравенства. Вариант 5.1.
- •Вариант 5.2.
- •Вариант 5.3.
- •Вариант 5.4.
- •Вариант 5.5.
- •Вариант 5.6.
- •Вариант 5.7.
- •Вариант 5.8.
- •Вариант 5.9.
- •Вариант 5.10.
- •6. Системы алгебраических уравнений. Рациональные неравенства Вариант 6.1
- •Вариант 6.2
- •Вариант 6.3
- •Вариант 6.4
- •Вариант 6.5
- •Вариант 6.6
- •Вариант 6.7
- •Вариант 6.8
- •Вариант 6.9
- •Вариант 6.10
- •7. Преобразование тригонометрических выражений. Вариант 7.1
- •Вариант 7.2
- •Вариант 7.3
- •Вариант 7.4
- •Вариант 7.5
- •Вариант 7.6
- •Вариант 7.7
- •Вариант 7.8
- •Вариант 7.9
- •Вариант 7.10
- •8. Тригонометрические уравнения Вариант 8.1
- •Вариант 8.2
- •Вариант 8.3
- •Вариант № 8.4
- •Вариант № 8.5
- •Вариант № 8.6
- •Вариант № 8.7
- •Вариант № 8.8
- •Вариант № 8.9
- •Вариант № 8.10
- •9. Показательные уравнения. Показательные неравенства. Вариант 9.1.
- •Вариант 9.2.
- •Вариант 9.3.
- •Вариант 9.4.
- •Вариант 9.5.
- •Вариант 9.6.
- •Вариант 9.7.
- •Вариант 9.8.
- •Вариант 9.9.
- •Вариант 9.10.
- •10. Логарифмические уравнения и неравенства Вариант № 10.1
- •Вариант № 10.2
- •Вариант №10.3
- •Вариант №10.4
- •Вариант №10.5
- •Вариант №10.6
- •Вариант № 10.7
- •Вариант 10.8
- •Вариант 10.9
- •Вариант 10.10
- •11. Логарифмические неравенства и системы показательных и логарифмических уравнений и неравенств. Вариант 11.1
- •Вариант 11.2
- •Вариант 11.3
- •Вариант 11.4
- •Вариант 11.5
- •Вариант 11.6
- •Вариант 11.7
- •Вариант 11.8
- •Вариант 11.9
- •Вариант 11.10
- •12. Текстовые задачи Вариант 12.1
- •Вариант 12.2
- •Вариант 12.3
- •Вариант 12.4
- •Вариант 12.5
- •Вариант 12.6
- •Вариант 12.7
- •Вариант 12.8
- •Вариант 12.9
- •Вариант 12.10
- •13. Начала анализа Вариант 13 .1
- •Вариант 13 .2
- •Вариант 13.3
- •Вариант 13 .4
- •Вариант 13 .5
- •Вариант 13 .6
- •Вариант 13.7
- •Вариант 13 .8
- •Вариант 13 .9
- •Вариант 13 .10
- •14. Геометрия Вариант 14.1
- •Вариант 14.2
- •Вариант 14.3
- •Вариант 14.4
- •Вариант 14.5
- •Вариант 14.6
- •Вариант 14.7
- •Вариант 14.8
- •Вариант 14.9
- •Вариант 14.10
- •15. Задачи с параметрами Вариант 15.1
- •Вариант 15 .2
- •Вариант 15.3
- •Вариант 15.4
- •Вариант 15.5
- •Вариант `15.6
- •Вариант 15.7
- •Вариант 15.8
- •Вариант 15.9
- •Вариант 15.10
- •Литература
- •Тематические тесты по математике
- •394006 Воронеж, ул. 20-летия Октября, 84
Вариант 5.9.
А1.
Решением неравенства
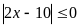 является
является
1) (-∞; 5); 2) [5; +∞); 3) ; 4) 5.
А2.
Решением неравенства
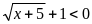 является
является
1) (-∞; -4]; 2) (-∞; -5]; 3) [-5; -4); 4) другой ответ.
А3.
Решением неравенства
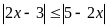 является
является
1) [0; +∞); 2) 2; 3) [2; +∞); 4) (-∞; 2].
А4.
Решением неравенства
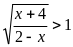 является промежуток
является промежуток
1) (-1; 2); 2) (-∞; -1); 3) [-1; 2); 4) (2; +∞).
А5.
Число целых решений неравенства
 ,
принадлежащих отрезку [-4; 5], равно
,
принадлежащих отрезку [-4; 5], равно
1) −7; 2) 14; 3) 5; 4) -10.
В1.
Число целых решений неравенства
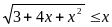 равно
равно
В2.
Число целых решений неравенства
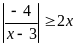 ,
принадлежащих отрезку
,
принадлежащих отрезку
[-4; 5], равно
В3.
Сумма целых решений неравенства
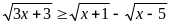 ,
принадлежащих отрезку
,
принадлежащих отрезку
[-3; 6], равна
В4.
Сумма целых значений, при которых
выполняется неравенство
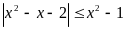 ,
принадлежащих промежутку [-3; 4), равна
,
принадлежащих промежутку [-3; 4), равна
В5.
Наибольшее решение неравенства
 равно
равно
Вариант 5.10.
А1.
Решением неравенства
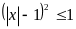 является
является
1) [0; 2]; 2) [-2; 0]; 3) [-2; 2]; 4)[-2; 0) (0; 2].
А2.
Решением неравенства
 является
является
1) [-5; -4]; 2) [-5; -4); 3) (-∞; -5]; 4) (-5; -4).
А3.
Решением неравенства
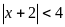 является
является
1) (-6; 2); 2) [-6; 2]; 3) (2; +∞); 4) (-∞; -6) (2; +∞).
А4.
Решением неравенства
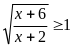 является промежуток
является промежуток
1) [-2; +∞); 2) (-∞; -1); 3) (-2; +∞); 4) (-∞; -2).
А5. Сумма целых решений неравенства , принадлежащих отрезку [-1; 5], равна
1) 5; 2) 15; 3) 9; 4) 14.
В1.
Сумма целых решений неравенства
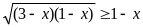 ,
принадлежащих отрезку [-4; 5], равна
,
принадлежащих отрезку [-4; 5], равна
В2.
Целое решение неравенства (или сумма,
если их несколько) равно
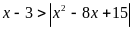
В3.
Сумма целых решений неравенства
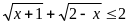 ,
принадлежащих отрезку
,
принадлежащих отрезку
[-3; 5], равна
В4.
Число целых значений, при которых
выполняется неравенство
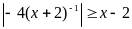 ,
принадлежащих отрезку [-4; 6], равно
,
принадлежащих отрезку [-4; 6], равно
В5.
Наименьшее целое решение неравенства
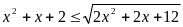 равно
равно
6. Системы алгебраических уравнений. Рациональные неравенства Вариант 6.1
А1. Если
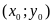 –
решение системы уравнений
–
решение системы уравнений
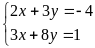 , тогда выражение
, тогда выражение
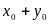 равно
равно
1) 2 ; 2) 0 ; 3) -2; 4) -3 ;
А2. Решением
неравенства
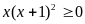 является
является
1) [ 0, + ∞) ; 2) {-1} [0 + ∞) ; 3) {-1} (0 + ∞) ; 4) (- ∞; 0)
А3. При каких значениях параметров а и b система уравнений
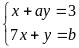 не имеет решений
не имеет решений
1)
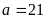 ,
b
,
b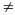
 ;
2) а
;
;
2) а
;
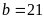 ;
3)
а
,
;
3)
а
,
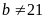 ;
4) а =
;
.
А4. Число целых решений неравенства
;
4) а =
;
.
А4. Число целых решений неравенства
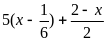 >
>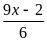 ,
принадлежащих отрезку
,
принадлежащих отрезку
[-7; 5], равно
4; 2) 5; 3) 6; 4) 9.
А5 . Решением
неравенства
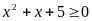 является
является
1) [-3; 2] ; 2) Ø; 3) ( - ∞, + ∞) ; 4) (-∞, -3) (2, + ∞)
B1.
Если (х0; у0) – решение
системы уравнений
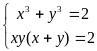 ,
тогда выражение х0у0 равно
,
тогда выражение х0у0 равно
B2.
Число целых решений неравенства
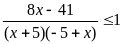 ,
удовлетворяющих
,
удовлетворяющих
условию
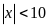 ,
равно
,
равно
В3. Если (х0;
у0) – решение системы
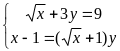 ,
тогда число
,
тогда число
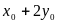 равно
равно
B4. Сумма целых решений неравенства
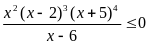 принадлежащих отрезку [-5; 7], равна
принадлежащих отрезку [-5; 7], равна
B5.
Число целых решений неравенства
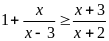 ,
принадлежащих отрезку [-3; 4], равно
,
принадлежащих отрезку [-3; 4], равно
