Задача 12. Вычислите определенные интегралы.
 5
5
1. òx5  x2 + 4dx
x2 + 4dx
0
2dx
5.ò0 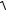 (5 - x2 )3
(5 - x2 )3
|
8 |
x |
2 |
+1dx |
|
|
7. |
ò |
|
|
|
|
3 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
x |
2 |
+ 4dx |
|
|
9. ò |
|
|
|
|
2 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
dx |
|
11. ò |
|
|
|
|
|
(81 + x |
2 |
) |
81 + x |
2 |
|
0 |
|
|
|
4 |
|
|
|
|
|
|
|
|
13. ò |
16 - x2 dx |
|
|
0 |
|
|
|
|
|
|
|
|
|
3 |
|
|
dx |
|
|
|
|
15. |
ò |
|
|
|
|
|
3 |
|
|
0 |
|
|
(1 + x2 ) |
|
7dx
17.ò2 x 2 + x2
2x4dx
19.ò
0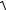 (8 - x2 )3
(8 - x2 )3
1
2. òx4  1 - x2 dx
1 - x2 dx
|
0 |
|
|
|
|
|
|
3 |
|
dx |
|
|
4. |
ò |
|
|
|
(9 |
|
|
3 |
|
|
0 |
+ x2 ) 2 |
|
5 |
|
1 |
|
|
6. |
ò |
|
|
dx |
|
x |
2 |
-1 |
|
2 x |
|
|
3dx
8.ò0 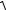 (4 - x2 )3
(4 - x2 )3
2x2dx
10.ò
0 16 - x2
16 - x2
1
2
12. òx2  1 - x2 dx
1 - x2 dx
0
|
4 |
3 |
dx |
|
|
|
14. |
ò |
|
|
|
|
|
|
|
3 |
|
|
|
0 |
|
(64 - x2 ) |
|
|
|
2 |
2 |
x2dx |
|
|
16. |
ò |
|
|
|
|
(16 - x |
2 |
) 16 |
- x |
2 |
|
0 |
|
|
|
18. 2ò3  4 + x2 dx x3
4 + x2 dx x3
 5
5
2dx
20.ò0 (4 - x2 ) 4 - x2
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
dx |
|
|
3 |
|
|
|
dx |
|
|
|
21. |
ò |
|
|
|
|
|
22. |
ò |
|
|
|
|
|
|
(1 |
- x |
2 |
) |
1 - x |
2 |
x |
2 |
4 - x |
2 |
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
23. |
ò |
|
|
|
dx |
|
24. |
òx |
2 |
16 - x |
2 |
dx |
|
3 |
x |
2 |
|
|
|
|
|
|
|
2 x |
|
|
-1 |
|
-4 |
|
|
|
|
|
|
|
|
|
25. |
2 |
|
|
|
- 3dx |
|
2 |
3 |
|
|
|
4 + x2 |
dx |
ò |
(1 |
- x |
2 |
) |
1 - x |
2 |
26. |
ò |
|
|
|
x |
4 |
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
x |
4 |
|
|
|
27. |
òx2 |
|
9 - x2 dx |
|
28. |
ò |
|
|
|
|
3 |
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
(1 - x2 ) |
|
|
|
1 |
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
29. |
òx4 |
|
4 - x2 dx |
|
30. |
ò |
|
9 - x2 dx |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Задача 13. Вычислите площадь фигуры, ограниченной линиями, заданными уравнениями в декартовых или полярных координатах .
1. |
y = 2x - x2 , y = -2x2 + 4x |
|
2. |
p = 4 cos 2j, p = 2,j ³ 2 |
3. |
y = sin 2 x, y = 0, x = |
p |
|
|
|
4. |
p2 = 3cos3j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
5. |
y = e1- x , y = 0, x = 0, x = 1 |
|
6. |
p = 2sin 2 2j |
|
|
|
7. |
y = x2 , x = y2 |
|
|
|
|
|
|
8. |
p = sin j - cosj |
|
|
|
9. |
y = sin 2 x × cos x, y = 0, x = |
p |
|
10. |
p = 4sin |
3j |
, p = 2,j ³ 2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
11. |
y = x2 |
4 - x2 , y = 0, x =1 |
|
12. |
p = 2 cosj, p = cosj |
|
13. |
y = ex |
-1, y = 0, x = ln 5 |
|
14. |
p = 2 - cosj |
|
|
|
15. |
y = |
1 |
, y = 0, x = e, x = e4 |
16. |
p = 2sin 3j |
|
|
|
|
|
x |
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
æ |
|
p |
ö |
17. |
y = ln x, y = ln |
|
x |
18. |
p = sin j, p = cosj,j Îç |
0; |
|
÷ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ø |
19. |
y = ex , y = e- x , x =1 |
|
20. |
p = 3 - sin j |
|
|
|
|
|
y = 2x - x |
2 |
+ 3, y |
= x |
2 |
|
- 4x + 3 |
|
p |
2 |
æ |
|
p |
ö |
|
|
21. |
|
|
|
22. |
|
= 3cosçj - |
|
|
÷ |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
23. |
y = x2tgx, y = 0, x = |
p |
|
|
24. |
p =1 + sin 2j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
25. |
y = 2x |
-1, y = |
× x(4 - x) |
26. |
p = 3 - sin j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
4 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
p ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
æ |
|
|
|
27. |
y = sin |
|
|
, y = cos |
|
, x |
= 0 |
28. |
p = 4 cos |
ç |
2j - |
|
|
÷ |
|
2 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
29. |
y = x2 , x + y = 2, x = 0 |
|
30. |
p = 3sin 4j |
|
|
|
|
Задача 14. Вычислите площадь фигуры, ограниченной линиями:
ìx = cost;
1.í
îy = 3 + sin t.
ìx = 6cost; |
2. í |
x = 3 3 при x ³ 3 3 . |
îy = |
3 sin t, |
3. |
ìx = 2(t - sin t ); |
|
y ³1,0 £ x £ 4p . |
í |
|
|
|
y =1 при |
|
îy = 2(1 - cost ), |
|
|
|
ì |
|
|
|
3 |
|
|
4. |
ïx = 2 +16 cos t; |
|
|
í |
|
3 |
|
x = 4 при x ³ 4 . |
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
îy = 2sin t, |
|
|
|
ì |
|
|
|
3 |
|
|
5. |
ïx = 2 |
2 cos t; |
|
|
í |
|
|
|
y = 2 при y ³ 2 . |
|
ïy = 4 |
2sin 3 t, |
|
|
|
î |
|
|
|
|
|
|
6. |
ìx = 3(t - sin t ); |
|
|
í |
- cost ), |
|
|
|
îy = 3(1 |
|
|
7. |
ìx = 6cost; |
y = 3 при |
y |
£ 3 . |
í |
|
|
|
|
îy = 2sin t, |
|
|
|
|
ì |
|
|
2 |
t; |
|
|
8. |
ïx =16 cos |
|
|
|
í |
3 |
|
|
|
|
|
|
ï |
t. |
|
|
|
|
|
|
|
|
|
|
|
îy = sin |
|
|
|
|
|
21. |
ìx = 4 cost; |
|
|
y = 3 при y ³ 3 . |
í |
|
|
|
|
|
|
|
îy = 9sin t, |
|
|
|
|
|
|
|
ì |
|
|
3 |
t; |
|
|
|
|
|
22. |
ïx = 5cos |
|
|
|
|
|
|
í |
|
3 |
|
|
|
|
|
|
|
|
ï |
|
t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îy = 5sin |
|
|
|
|
|
|
23. |
ìx = 3cost; |
|
y = 4 |
3 при |
y ³ 4 3 . |
í |
|
|
|
|
|
|
îy = 8sin t, |
|
|
|
|
|
|
|
ì |
|
2 cost; |
|
|
|
24. |
ïx = 2 |
|
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
ï |
|
2 sin t, |
|
|
|
|
îy = 3 |
|
|
|
25. |
ìx = 2 cost; |
|
|
y = 3 при |
y |
³ 3 . |
í |
|
|
|
|
|
|
|
îy = 6sin t, |
|
|
|
|
|
|
|
26. |
ìx = 3cost; |
|
y =1 при |
y ³1. |
í |
|
|
|
|
|
|
îy = 2sin t, |
|
|
|
|
|
|
27. |
ìx = t; |
ìx = t; |
|
|
|
í |
2 , |
í |
|
= 3 - t3. |
|
|
|
îy = t |
îy |
|
|
28. |
ìx = 2 cost; |
|
x = 1 при x ³ 1 . |
í |
|
|
|
|
|
|
îy = 6sin t, |
|
|
|
|
|
|
|
ì |
2 cos |
3 |
t; |
|
|
|
29. |
ïx = |
|
=1 при y ³1. |
í |
|
|
|
|
|
3 |
y |
|
ï |
|
|
|
|
|
|
|
|
|
|
|
2 sin t, |
|
|
|
|
îy = 2 |
|
|
|
30. |
ìx = 2(t - sin t); |
|
|
|
í |
|
|
|
|
|
|
y =1 при y ³1,0 £ x £ 4p |
îy = 2(1- cos t),
.
Задача 15. Вычислите длину дуги кривой.
1.y2 = 4x от ее вершины до точки M (1;2).
2.y = 2 x при 0 £ x £ 1 .
x при 0 £ x £ 1 .
|
|
ìx = 2(t sin t + cost); |
при 0 £ t £ |
p |
|
3. |
í |
|
. |
|
2 |
|
|
îy = 2(sin t - t cost), |
|
|
4. |
p = 1 + sin j при |
p |
£ j £ |
p |
. |
|
2 |
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
5. |
x = |
2 |
y |
|
при 0 £ y £ 3 . |
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
6.y = 4 - x2 между точками ее пересечения с осью Оx.
7.y = ln(x3 -1) при 2 £ x £ 3 .
8. y = ex при 1 ln £ x £ 1 ln 8 .
22
9.p = 3(1 - sin j) при 0 £ j £ p .
2
|
|
y = |
2 + |
ex |
+ e-x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
|
|
|
|
|
|
при 0 £ x £ 2 . |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
11. |
y = |
1 - x2 + arccos x при 0 £ x £ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
12. |
y = ex + 3 при ln |
8 £ x £ ln 15 . |
|
|
ì |
|
t |
cost; |
|
|
|
|
|
p |
|
|
ïx = e |
|
£ t |
|
|
|
|
|
13. |
í |
|
|
|
|
|
|
|
при 0 |
£ |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
t |
|
|
|
|
2 |
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îy = e sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14. y = ln sin x при |
p |
£ x £ |
p |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
2 |
|
|
|
|
|
15 |
|
|
15. |
y = arcsin x - 1 - x2 |
при 0 £ x £ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
16. |
p = 2sin 3 |
j |
при 0 £ j £ |
p |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
ì |
|
|
|
|
|
3 |
t; |
|
|
|
|
|
|
p |
|
|
ïx = 3cos |
|
|
|
|
|
|
|
|
17. |
í |
|
|
|
|
3 |
|
при 0 £ t |
£ |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
t |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îy = 3sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18. |
y = ln cos x при 0 £ x £ |
p |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
19. |
p = |
|
3ej |
|
при 0 £ j £ |
p |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20. y = 1 x2 - 1 ln x при 1 £ x £ 2 . |
4 |
2 |
|
|
ì |
2t |
sin t; |
|
|
|
p |
|
|
ïx = e |
|
£ t £ |
|
21. |
í |
|
при 0 |
|
. |
|
2t |
4 |
|
|
ï |
cost |
|
|
|
|
|
|
|
|
|
|
|
|
|
îy = e |
|
|
|
|
|
|
|
22. |
p = 3(1 - cosj) при |
2p |
£ j £ 2p . |
|
|
|
|
|
|
|
3 |
|
|
|
23.y = e2 x при 0 £ x £ 1 .
24.y = ln x при  3 £ x £
3 £ x £  8 .
8 .
25. |
y = 3 - ln sin x при |
p |
£ x £ |
p |
. |
3 |
|
|
|
|
|
|
|
|
|
2 |
|
|
ì |
|
3 |
t; |
p |
|
|
|
|
p |
|
ïx = 6cos |
|
|
£ t |
£ |
26. |
í |
|
|
при |
|
|
|
|
. |
|
3 |
4 |
|
2 |
|
|
ï |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îy = 6sin |
|
|
|
|
|
|
|
|
|
|
|
|
27.y2 = (x -1)3 от точки M (1;0) до точки N (2;-1).
28.y = ex при 0 £ x £ 1 .
29. p = 6cos3 |
j |
при 0 £ j £ |
p |
. |
|
|
3 |
2 |
|
|
|
ì |
|
2 |
t; |
|
p |
|
|
ïx = 2cos |
|
£ t £ |
|
30. |
í |
|
|
при 0 |
|
. |
|
2 |
4 |
|
|
ï |
t |
|
|
|
|
|
|
|
|
|
|
îy = 2sin |
|
|
|
|
|
Задача 16. Вычислите объем тела, образованного вращением вокруг указанной оси координат фигуры, ограниченной заданными линиями.
1.y = 2sin x, y = 0 при 0 £ x £ p , вокруг оси Ox.
2.y3 = 4x2 , y = 2 , вокруг оси Oy.
3.2 y2 = x3 , x = 4 , вокруг оси Ox.
4.y = x2 , y = 4, вокруг оси Oy.
ìx = 3cost;
5. í вокруг оси Ox.
îy = 5sin t,
6.y = x2 , x = y2 , вокруг оси Oy.
7.y =1 - cos 2x, y = 0, x = p , вокруг оси Ox.
2
8. y =1 - x2 , x + y =1, вокруг оси Oy. 2
9.y = x2 +1, x = ±2, y = 0, вокруг оси Ox.
10.xy = 4, y =1, y = 2, x = 0, вокруг оси Oy.
11.y = 2x , y = 5 + 3x , вокруг оси Ox.
|
|
|
|
|
|
|
|
|
|
|
4 |
|
12. |
|
x2 |
- |
y2 |
|
|
|
=1, y = ±6, |
вокруг оси Oy. |
4 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ì |
|
|
|
|
|
|
|
3 |
t; |
|
13. |
ïx = 3cos |
|
|
í |
|
|
|
|
|
|
3 |
вокруг оси Ox. |
|
ï |
|
|
|
|
|
|
t, |
|
|
|
|
|
|
|
|
|
|
|
|
îy = 3sin |
|
|
|
14. |
|
y2 |
= 4 - x, x = 0, вокруг оси Oy. |
15. |
|
y = ex , x = 0, x = ln 2, вокруг оси Ox. |
16. |
|
y = x3 , x = 0, y = 8, вокруг оси Oy. |
17. |
(y -1)2 |
= x, x = 1, вокруг оси Ox. |
18. |
ìx = cost; |
вокруг оси Oy. |
í |
|
|
|
|
|
|
|
|
|
îy = 3sin t, |
|
19. |
|
y = x2 , x = y2 , вокруг оси Ox. |
20. |
|
y2 |
= (x + 5)3 , x = 0, |
вокруг оси Oy. |
21. |
ìx = 3(t - sin t); |
= 0, 0 £ x £ 6p, вокруг оси Ox. |
í |
|
|
|
|
|
|
|
|
y |
|
îy = 3(1 - cost), |
|
|
ì |
|
|
|
|
|
3 |
t; |
|
22. |
ïx = cos |
|
|
í |
|
|
|
|
3 |
|
|
вокруг оси Oy. |
|
ï |
|
|
|
|
t, |
|
|
|
|
|
|
|
|
|
|
îy = sin |
|
|
|
23.xy = 4, y = 0, x =1, x = 4, вокруг оси Ox.
24. x + y = 4, y = 0, x = 0, вокруг оси Oy.
x + y = 4, y = 0, x = 0, вокруг оси Oy.
25.y = ex , y =1, x =1, вокруг оси Ox.





 5
5 x
x (
(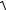 (
( 1
1 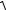 (
( 16
16  1
1 
 5
5


 2 cos
2 cos
 x
x 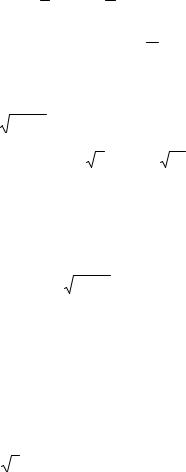

 3
3  8
8 
