DQ = 0, 24RI02 sin2 wtdt .
Таким образом, количество тепла за период T = 2p равно w
T |
2p |
|
|
|
w |
|
|
Q = òdQ = 0, 24RI02 |
ò sin 2 wtdt = |
|
|
0 |
|
|
0 |
|
|
|
|
|
2p |
|
|
|
|
|
|
w |
|
|
|
p RI |
2 |
|
= 0,12RI02 ò (1- cos 2wt)dt = 0, 24 |
0 |
. |
w |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
8.26. Вертикальный вращающийся вал веса Р и радиуса а опирается на подпятник. Найти работу силы трения между основанием вала и прилегающей к ней поверхностью опоры при одном обороте вала.
Решение. Сила трения между основанием вала(пятой) и прилегающей к ней поверхностью опоры (подпятником) равна
F = µрs, где р — давление вала на поверхность опоры в рассматриваемой точке, отнесенное к единице площади опоры, µ - коэффициент трения. Поскольку вес вала ,Рто давление на единицу площади опоры равно
|
|
p = |
|
P |
. |
|
|
|
|
|
pa 2 |
|
|
|
|
|
|
|
|
|
Рассматривая p как |
функцию радиуса-вектораr при |
вычислении |
полного |
давления, воспользуемся |
|
методом |
суммирования бесконечно малых элементов. |
|
|
Разобьем |
поверхность |
трения |
на |
элементарн |
концентрические кольца, так что все давление сложится из |
элементарных |
давлений, |
соответствующих |
|
отдельным |
кольцам. Рассмотрим кольцо, ограниченное окружностями r и r+dr. Площадь этого кольца приближенно равна2πrdr. Сила трения от кольца шириной dr, удаленного от центра вала на r,
равна 2mP rdr . a 2
Работа силы трения на элементарном кольце при одном
обороте 2p r равна dA = 4pmP r 2 dr . Таким образом, полная a 2
работа силы трения будет
a |
4pmP |
|
2 |
|
4pmP a3 |
A = ò |
|
|
r |
|
dr = |
|
|
|
|
a |
2 |
|
a |
2 |
|
3 |
0 |
|
|
|
|
|
|
|
8.27. Найти |
силу |
притяжения, с |
|
которой |
действует |
|
материальный стержень длины l |
и массы М на материальную |
|
точку массы m , находящуюся на одной прямой со стержнем |
|
на расстоянии а от одного из его концов. |
|
|
|
|
|
|
Решение. Сила F взаимодействия |
двух |
точечных |
масс |
|
определяется законом Ньютона F = |
kmM |
, |
где r - расстояние |
|
r 2 |
|
|
точками, т и М — массы |
|
|
|
|
|
|
|
между |
|
точек, |
k |
- коэффициент |
|
пропорциональности. |
|
|
|
|
|
|
|
|
|
|
|
|
Масса |
единицы |
длины |
стержня(линейная |
плотность) |
|
M / l = const |
— величина |
постоянная. Выделим |
элемент |
|
стержня длиной dx, отстоящий от его конца на расстояниих. |
|
Сила |
взаимодействия |
выделенного |
|
элемента |
с |
точечной |
|
массой |
т |
равна |
dF = |
|
kmM |
dx . |
Отсюда |
вся |
сила |
|
(a + x)2 l |
|
|
|
|
|
|
|
|
|
|
|
|
|
притяжения будет
|
l |
kmM |
|
kmM 1 |
|
F = ò0 |
dx = - |
|
l(a + x)2 |
l |
|
a + x |
3.9. Вычисление определённых интегралов численными методами
Пусть |
требуется |
найти |
|
приближённое |
значен |
|
|
|
|
b |
|
|
|
|
|
определенного |
интеграла ò f (x )dx . |
Для |
этого |
разобьём |
|
|
|
|
a |
|
|
|
|
|
интервал интегрирования [a, b] |
точками x1 , x2 ,..., xn-1 |
на n |
|
равных частей h = |
b - a |
, x0 |
= a , |
xn = b |
и вычислим значения |
|
|
|
|
|
n |
|
|
|
|
|
|
подынтегральной функции в точках деления
y0 = f (a), y1 = f (x1 ), y2 = f (x2 ),..., yn-1 = f (xn-1 ), yn = f (b).
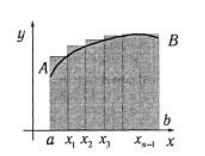
Представляя определённый интеграл в виде площади криволинейной трапеции, используют одну из следующих приближённых формул.
1°. Формула прямоугольников
b |
|
|
|
|
|
|
|
n-1 |
|
|
|
ò f (x )dx = h(y0 + y1 + y2 + ... + yn-1 )+ Rn = hå yi + Rn |
|
(1) |
a |
|
|
|
|
|
|
|
i=0 |
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
n |
|
|
|
|
ò f (x )dx = h(y1 + y2 + ... + yn ) |
+ Rn |
= hå yi |
+ Rn |
|
(2) |
|
a |
|
|
|
|
|
|
i=1 |
|
|
|
где |
Rn = |
h2 |
|
¢¢ |
(x ) |
- |
предельная |
абсолютная |
|
|
24 |
(b - a)f max |
|
|
|
|
|
|
|
|
|
|
погрешность |
|
формулы |
|
|
|
¢¢ |
(x ) |
- |
|
|
прямоугольников; fmax |
наибольшее значение производной в интервале [a, b]. |
|
|
|
Геометрическая |
площадь |
криволинейной |
|
трапеции |
aABb |
(рис. |
3.66), которая |
соответствует |
определённому |
интегралу, записывается суммой площадей заштрихованных прямоугольников. Формула (1) соответствует схеме деления
193
для вычисления приближённого значения недостатку. Формула (2) соответствует схеме приближённое значение интеграла по избытку.
|
|
|
|
|
|
Рис. 3.66 |
|
|
|
2°. Формула трапеций |
|
|
|
|
|
b |
æ y |
0 |
+ y |
n |
|
|
|
ö |
|
|
ò f (x )dx = h ç |
|
|
+ y1 |
+ y2 |
+... + yn-1 |
÷ |
+ Rn |
= |
|
|
2 |
|
a |
è |
|
|
|
|
|
|
ø |
|
|
æ y |
0 |
+ y |
n |
n-1 |
ö |
|
|
h ç |
|
|
+ å yi ÷ |
+ Rn |
, |
|
|
2 |
|
è |
|
|
|
i=1 |
ø |
|
|
где |
Rn |
= h |
2 b - a |
¢¢ |
(x ) - погрешность формулы трапеций, |
|
|
12 |
f max |
|
|
|
|
|
x Î[a, b].
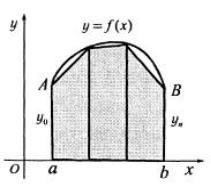
Геометрическая площадь криволинейной трапеции aABb
(рис. 3.67) заменяется площадей заштрихованных трапеций.
Рис.3.67
2°. Формула Симпсона (параболических трапеций)
|
b |
|
( |
|
|
h |
|
|
|
|
|
|
|
( |
|
|
|
n-1 ) |
|
|
|
|
|
|
ò |
f |
x dx = |
é y |
+ y + 4 |
y + y |
+... + y |
+ 2 |
y |
+ y +... + y |
ù + |
|
|
|
|
|
) |
3 |
ë |
0 |
|
n |
|
|
|
1 |
3 |
|
|
(2 |
4 |
n-2 )û |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
æ |
|
|
|
n |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ Rn |
= |
|
|
ç y0 + yn |
+ |
4åy2k -1 ÷ |
+ Rn |
, |
|
|
(4) |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
k =1 |
ø |
|
|
|
|
|
|
где |
|
Rn |
= h |
4b - a |
f max(IV )(x ) - погрешность формулы; n |
- |
число |
|
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чётное; x Î[a, b]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Геометрическая |
|
|
|
площадь |
каждой |
|
пары |
|
вертикальных |
|
криволинейных трапеций является площадью параболической |
|
трапеции (рис.3.68), |
т. е. каждый |
участок |
кривой y = f (x) |
заменяется дугой параболы y = x 2 + px + q , проходящей через три точки кривой с абсциссами xi , xi +1 , xi+2 .
Рис. 3.68
Очевидно, что чем больше n , тем приближенное значение определённого интеграла точнее. При одном и том жеn
формула |
|
|
трапеции |
точнее |
|
формулы |
прямоугольников, |
формула |
|
|
Симпсона |
точнее |
|
формулы |
трапеции. Есл |
предельная |
|
абсолютная |
погрешность |
|
заданаe > 0 , |
то |
параметр |
h |
|
или число разбиенийn могут |
быть |
найдены из |
неравенства |
|
Rn |
|
< e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При вычислении значений определённых интегралов на |
ЭВМ |
погрешность |
целесообразно |
|
оценивать |
|
методом |
удвоения |
|
шага |
вычислений. Полагая |
n = k и |
h = |
b - a |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вычисляем значения искомого интеграла J1, |
k - чётное. Затем |
удваиваем |
число |
разбиенийn = 2k |
|
и |
h2 |
= |
b - a |
, находим |
|
|
|
|
интеграла J 2 . |
|
|
J2 - J1 |
|
|
|
2k |
|
|
|
|
значение |
|
|
Если |
|
|
|
< e , |
то |
расчёт |
|
|
|
|
заканчивается, иначе снова удваиваем разбиение.
1 |
|
9.1. Вычислить интеграл ò |
5 + x3 dx , разбивая интервал |
0 |
|
интегрирования на 10 равных |
частей, по формулам: |
а) прямоугольников; б) трапеций; в) Симпсона. Оценить погрешности результатов.
Абсолютная ошибка этого приближения равна Rn = 0,0004. б) По формуле трапеций (3) имеем
|
æ 4,6855 |
0 |
ö |
|
J = 0,1ç |
|
+ å yi |
÷ = 2,291. |
|
2 |
|
è |
i=1 |
ø |
Абсолютная ошибка результата равна
Rn = 0,011,0716 = 0,0009 . 12
в) По формуле Симпсона получим
J = 0,1 (2,2361 + 2,4494 + 4 ×11,4472 + 2 ×9,1198)= 2,2905.
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
нахождения |
абсолютной |
погрешности |
вычисляем |
f(1IV) = 1,6244 . Абсолютная ошибка равна всего лишь |
|
|
|
|
|
|
Rn = |
0,0001 |
×1,6244 = 0,0000009. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
9.2. |
По |
|
формуле Симпсонавычислить приближённое |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
значение интеграла ò |
sin xdx |
|
|
с точностью до 0,0001. |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
x +1 |
|
|
|
|
|
|
Решение. Сначала определим, на какое число частейn |
следует |
разбить интервал |
|
|
интегрирования[0,p ]. Поскольку |
требуется точность 10-4, то имеем |
|
|
|
|
|
|
|
|
|
|
|
(b - a)5 |
|
fmaxIV <10-4 . |
|
|
|
|
|
|
|
|
|
|
|
180n4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
fmaxIV |
|
= 0,039 ; |
|
a = 0 , |
|
b = p = 3,14159 , то окончательно |
получим n |
4 |
> |
p 5 ×0, 039 ×104 |
или n > 5,1. |
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ближайшее четное число n = 6 . Находим точки деления xi |
и |
соответствующие значения функции y = |
sin x |
|
|
x +1 |
|
|
|
|
|
|
|
x0 |
= 0, |
|
|
|
|
|
y0 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
p |
, |
y |
= 0,3283 |
|
|
|
|
|
|
|
|
|
|
|
1 |
6 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
= |
|
p |
, |
y2 |
= 0,4235 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
x3 |
= |
|
p |
, |
y3 |
= 0,3891 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x4 |
= |
|
2 |
|
p , |
y4 |
= 0,2803 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
x5 |
= |
5 |
p , |
y5 |
= 0,1382 |
|
|
|
|
|
|
|
|
x6 |
6 |
|
|
|
|
|
y6 |
|
|
|
|
|
= p, |
= 0. |
|
|
Подставляя в формулу Симпсона(4), находим значения |
интеграла с точностью 10-4 |
|
|
|
|
p |
sin xdx |
= 0.1744(4 × 0,8556 + 2 × 0,7038) = 0,84235 . |
|
ò |
|
|
|
0 |
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Современная |
вычислительная |
техника |
позволяе |
вычислять интегралы с любой точностью, необходимой для практического использования результатов расчёта.
4. ЗАДАЧИ ДЛЯ ТИПОВОГО РАСЧЕТА
Задача 1. Найдите неопределенные интегралы.
1. |
ò6 |
|
(x + 4)5 dx |
3. |
ò |
|
|
|
|
dx |
|
|
|
2 |
|
|
|
|
2 - 2x |
|
|
5. |
ò |
|
|
dx |
|
|
|
|
|
|
7x |
2 |
+ 7 |
|
|
|
|
|
|
|
|
|
|
7. |
ò |
|
|
x3 |
|
|
dx |
4 |
- x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
9. |
ò(x -1)x |
|
dx |
3 |
11. ò |
|
|
dx |
|
|
|
|
|
4x |
2 |
|
- 4 |
|
|
|
|
|
|
|
13. |
òsin (2 - 4x)dx |
15. |
ò |
dx |
2 |
|
|
(5x -1) +1 |
17. ò42-3x dx
dx
19. ò sin 2 (2 - 3x)
dx
21. ò sin 2 (1 - 2x)
2. ò |
|
æ1- x ö |
2 |
|
|
|
|
ç |
|
|
|
|
|
÷ |
dx |
|
|
x |
|
|
|
|
è |
|
|
|
ø |
|
|
|
|
4. |
ò |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
3x |
2 |
-9 |
|
|
|
|
|
|
|
|
|
|
|
|
6. ò |
(arctgx)3 |
dx |
|
|
|
|
|
|
|
|
|
|
1+ x |
|
|
|
|
8. ò(3x - 7)17dx |
10. |
ò 5 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 - 2x |
|
|
|
12. |
ò |
|
|
|
|
|
dx |
|
2 |
|
|
|
|
|
|
|
|
8 + 4x |
|
|
|
14. |
òcos(1- 2x)dx |
16. |
ò21-4 x dx. |
|
|
|
18. |
ò |
|
|
|
|
dx |
|
|
|
|
|
|
|
5 |
+ 3x |
|
|
|
|
|
|
|
|
|
|
|
|
20. |
ò21-x dx |
|
|
|
|
22. |
ò |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
cos |
2 |
4x |
|
|
|
|
|
|
|
|
|
|
|
|
24. |
ò |
|
|
|
|
|
dx |
|
|
|
cos2 (1 - 3x) |
|