Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1733

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2412 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Если t Î[-2, 0] , то y £ 0 ; если t Î[0, 2] , то y ³ 0 . Точка

(6,0) является точкой самосопряжения кривой. Следовательно, кривая имеет форму петли (рис. 3.14).

Рис.3.14

Вследствие симметрии фигуры относительно осиx, достаточно найти половину площади; тогда вся площадь по формуле (6) будет равна

2	2			æ		t	3		t	5	ö	2		512

S = 2ò0	t (4 -t2 )4tdt = 8ò0	(4t 2	-t 4 )dt = 8	ç	4			-			÷		=		.

				è	3			5			ø	0	15


2.3. Найти площадь, ограниченную					линиями: а) одним
витком	спирали		Архимедаr = aj ;			б) кардиоидой
r = a (1+ cosj ); в)		лемнискатой		(x2 + y2 )2 = 2a2 (x2 - y2 );			г)
окружностями		r = a cosj		и	r =	3a sin j ;	д)
x3 + y3 - 3axy = 0 (декартов лист).

Решение. а) Один виток спирали Архимеда описывается концом полярного радиуса при изменении полярного углаj от 0 до 2p . По формуле (5) находим

	1	2p	2 2		a2		3	2p		4		3		2
								2p

S =		ò0	a j	dj =		j			=		p		a		.
S =	2	ò0	a j	dj =	6	j		0	=	3	p		a		.
	2				6					3

111

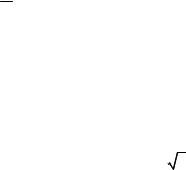
б)

Поскольку

кардиоида

симметрична

относительно

полярной оси, то достаточно найти половину ее площади,

когда полярный угол j изменяется от 0 до p . Отсюда по фор-

муле (5) имеем

p æ

S = 2 ×

ò0 a

(1+cosj)

dj = a

ò0

ç1

+2 cosj +

(1 +cos 2j )÷ dj =

= a

j + 2sinj +

sin 2j ÷

p a

в) Лемниската симметрична относительно координатных осей и делится ими на четыре равные части. Если перейти к полярным координатам x = r cosj, y = r sinj , то уравнение лемнискаты в полярных координатах примет вид

r2 = 2a2 cos 2j .

Четвертой части площади соответствует изменение поляр-

ного угла от 0 до p . Отсюда вся площадь по формуле (5) 4

будет равна

S = 4 ×

ò4 2a2 cos 2jdj = 2a2 sin 2j

= 2a2 .

г)

Решая

совместно уравнения

окружностей,

находим

точку

(рис.

3.15) их пересечения

Aç a

÷ .

Искомая

площадь равна сумме площадей двух сегментов OBA и OCA .

112

Рис.3.15

Дуга ОСА описывается концом полярного радиуса боль-

шой окружности при изменении полярного угла j от 0 до p , 6

следовательно

SOCA =

3a2 sin2 jdj =

(1- cos 2j )dj =

ò06

æ p

2 æ

j -

sin 2j

÷.

Дуга ОBА описывается концом полярного радиуса мень-

шей

окружности

при

измененииj

от

до

следовательно,

SOBA

a2 cos2 jdj =

(1+ cos 2j )dj =

4 ò

a2 æ

a2 æ p

3 ö

j +

sin 2j

÷.

Таким образом, искомая площадь

S =

SOCA + SOBA

3 ÷ .

y = r sinj

д) Переходя к полярным координатам x = r cosj ,

в уравнении декартова листа, получим

113

r =					3a sinj cosj						.			Так				как		петля					кривой соответствует
r =											.			Так				как		петля					кривой соответствует
				sin3 j + cos3 j
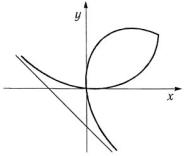
изменению							полярного										углаj		от				0	до		p			(рис.	3.16), то
изменению							полярного										углаj		от				0	до			2		(рис.	3.16), то
площадь будет равна																											2
площадь будет равна
													1				p	9a2 sin2 j cos2 j
									S =				1		ò02			9a2 sin2 j cos2 j								dj .
									S =				2		ò02			(sin3 j + cos3 j )2								dj .
Деля числитель и знаменатель на cos6 j , получим
					p												p			3										p
																				3
				2			2										2	d 1+ tg j												2		2
9			2	2			2					3				2	2	(					)		3			2	1	2	3a	2
9			2	ò		tg jdtgj						3				2	ò	(					)		3			2	1		3a		.
S =		a								=				a										= -		a				=
S =	2	a				(	3	)	2	=		2		a				(	3		)	2		= -	2	a			1+ tg3j	=	2
				0 1			+ tg j										0	1+ tg j												0

Рис.3.16

3.3. Объем тела

1°. Объем тела по площадям его параллельных сечений. Пусть известна площадь S(x) любого сечения тела плоскостью перпендикулярной оси x (рис. 3.17). Если x - расстояние сечения от начала координат, то при изменении x на величину dx дифференциал объема тела равен объему прямого цилиндра с высотой dx и площадью основанияS(x), т.е. dV = S (x )dx .

Объем всего тела выражается интегралом

114

V = òab S (x )dx ,

(1)

где a, b - левая и правая границы тела

Рис.3.17

2°. Если тело образовано вращением вокруг оси Ox криво-

линейной трапеции aABb (рис. 3.18), то	любое его	сечение,
перпендикулярное к оси Ox , будет круг,	площадь	которого
равна p y2 . Объем тела вращения вычисляется по формуле
V = p òab y2dx .		(2)

Рис.3.18

Если тело образуется вращением криволинейной трапеции вокруг оси Oy , то объем тела находится по формуле

V = p òc x2dy , (3)

где с и d - ординаты границ тела.

Если тело образовано вращением вокруг оси Oy криволинейной трапеции aABb , то элемент объема равен объему тела, образованного вращением вокруг оси Oy прямоугольника со сторонами y и dx отстоящего от оси Oy на расстоянии х. Объем тела вращения в этом случае равен

115

V = 2p òab xydx .

(4)

В более общих случаях объемы тел, образованных вра-

щением

криволинейных трапеций,

ограниченных

кривыми

y1 = f1 (x)

и y2

= f2 (x) , если

f1 (x) < f2 (x) , и прямыми x = a ,

x = b , вокруг

координатных

осейOx , Oy , соответственно

равны

= p ò(y12 - y22 )dx и Vy = 2p òx ( y2 - y1 )dx .

(5)

Если кривая задана параметрические, то, в приведенных

формулах вычисления объема тел вращения, следует сделать

соответствующую замену переменной интегрирования.

3°.

Если

криволинейный

сектор

вращается

вокруг

полярной оси и ограничен кривой r = r (j ) и лучами j = a ,

j = b , то объем тела вращения определяется по формуле

V =

p òr3 sin jdj .

(6)

3.1. Найти объем трехосного эллипсоида

=1 .

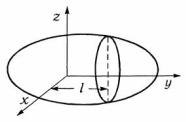
Решение. В сечении плоскости, перпендикулярной к оси у и отстоящей от начала координат на расстоянииl, будет эллипс (рис. 3.19).

Рис.3.19

Подставляя вместо y в уравнение эллипсоидаl, находим уравнение проекции эллипса на плоскость xz

116

= 1.

l 2

ç1

ç1-

Полуоси

эллипса

будут, соответственно,

C 1-

l 2

а его площадь

в функции переменной l

равна

S (l )= pac ç1

÷ .

Таким образом, по формуле (1) искомый объем равен

b æ

pac

)dl =

pac æ 2

V =pac òç1-

÷dl =

-l

çb l -

pabc .

-b è

-b

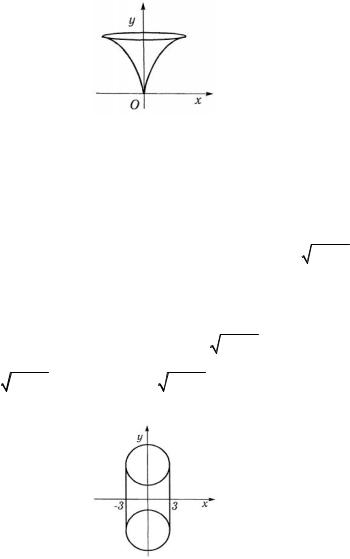
3.2. Два круговых цилиндра радиусаr пересекаются под

прямым

углом.

Найти

объем

тела, ограниченного

этими

цилиндрами.

Решение. На рис. 3.20 показана восьмая часть интересующего нас объема. В сечении искомого тела плоскостью, проведенной на расстоянии y от начала координат перпендикулярно к оси Oy , получается квадрат ABCD. Из треугольника АВО

сторона	квадрата	равна AB = r2 - y2 . Площадь квадрата в
функции	у будет	S (y ) = r 2 - y2 .	Отсюда,					по формуле (1)
имеем
	r	æ		y	3	ö	r		16
	r	æ			3	ö	r
	V = 8ò(r 2 - y2 )dy = 8çr 2 y -					÷		=		r3 .
	V = 8ò(r 2 - y2 )dy = 8çr 2 y -					÷		=		r3 .
	0	è	3			ø	0	3
	0	è				ø	0

117

Рис.3.20

3.3. Найти объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной кривой y = xex и прямыми у =0

и x = 1.

Решение. Сделаем чертеж (рис. 3.21) и воспользуемся формулой (2), тогда

V = p òx2e2 xdx .

Интегрируя дважды по частям, получим

2 x

2 2 x

2 x

V = p ç

ò0 xe

= p ç

x e

(xe

- ò0 e

dx )÷

çæ x2 - x +

÷öe2 x

(e2 -1).

Рис.3.21

3.4. Найти объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривой y2 = 4x и прямыми

x = 0 и y = 4 .

118

Решение. Сделаем чертеж (рис.	3.22) и воспользуемся
формулой (3), тогда
4	4
4	4
V = p ò0 4xdx = 2p x2	0	= 32p .
V = p ò0 4xdx = 2p x2	0

3.5. Найти объем	Рис.3.22
	кольца (тора), образованного

вращением окружности x2 + (y - 4)2 = 9 вокруг оси Ox .

Решение. Центр окружности сдвинут на четыре единицы вверх, а радиус окружности равенR = 3 (рис. 3.23). Решая уравнение окружности относительно y , находим уравнение

верхней	и нижней дуги полуокружностиy = 4 ±				9 - x2 .
				1,2
Объем	тора	представим	как	разность	тел , вращени
ограниченных этими окружностями. Учитывая симметрию
относительно оси Oy , будем иметь
V = 2p ò03 (y12 - y22 )dx = 2p ò03 (25 - x2 + 8 9 - x2 -
-25 +8 9 - x2 + x2 )dx =16p ò03			9 - x2 dx.

Рис.3.23

119

Сделаем

замену:

x = 3sin t, dx = 3costdt ;

при

x = 0,t = 0 ;

при x = 3, t =

. Тогда получим

(1 + cos 2t )dt =

V =16p ò02

9 cos2 tdt = 72p ò02

= 72p

çt +

sin 2t ÷

36p

3.6. Найти объем тела, образованного вращением вокруг

оси Ox фигуры, ограниченной

полуокружностью x2 + y2 = 1

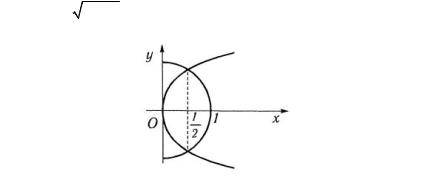
(при x>0) и параболой y = -x .

Решение.

Сделаем

чертеж (рис. 3.24)

из решения

системы

ïìy2 =

1- x

îy

найдем абсциссу точки

пересечения кривых: 2x2 + 3x - 2 = 0 ;

x =

-3 ± 9 +16

-3 ± 5

; x =

1,2

Рис.3.24

Поскольку криволинейная трапеция, которая вращается вокруг оси Ox , ограничена различными кривыми, то, вычисляя объем тела вращения по формуле(2), представим его в виде суммы двух интегралов

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2412 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.9 Mб3Учебное пособие 1729.pdf
#
30.04.2022311.71 Кб2Учебное пособие 173.pdf
#
30.04.20221.9 Mб3Учебное пособие 1730.pdf
#
30.04.20221.92 Mб8Учебное пособие 1731.pdf
#
30.04.20221.92 Mб2Учебное пособие 1732.pdf
#
30.04.20221.92 Mб4Учебное пособие 1733.pdf
#
30.04.20221.93 Mб4Учебное пособие 1734.pdf
#
30.04.20221.93 Mб4Учебное пособие 1735.pdf
#
30.04.20221.93 Mб8Учебное пособие 1736.pdf
#
30.04.20221.93 Mб12Учебное пособие 1737.pdf
#
30.04.20221.93 Mб6Учебное пособие 1738.pdf