Учебное пособие 1733

m =

1

b d

(M

)ydS =

1

b d (M

)y2dx,

2

2

x

ò

ò

a

a

(3)

1

b d

1

b d

m

=

(

M

xdS =

(

M

xydx,

y

2

ò

)

2

ò

)

a

a

если

известны

площади

поперечных

сечений

параллельных этой плоскости S(x) в функции расстояния x от

нее, при

плотности,

равной

единице, определяется

интегрированием статического момента элементарного слоя

тела на расстояниих от

плотности dm = xS(x)dx в заданных

пределах

b

myz

= ò xS(x )dx .

(4)

a

Статический

момент

тела

вращения

относительно

плоскости, перпендикулярной оси вращения х, определяется

по формуле

b

myz

= p ò xy2dx .

(5)

a

кривойу = f(x)

Если

поверхность образована вращением

(a £ x £ b)

вокруг

оси Ох

(рис. 3.37) и

поверхностная

плотность

ее

равна

единице, то

статический

момент

относительно плоскости,

перпендикулярной

оси вращения,

находится

интегрированием

элементарного

кольцевого слоя

2pydl в заданных пределах

b

b

myz = 2p ò xydl = 2p òxy 1 + (y¢ )2 dx

(6)

a

a

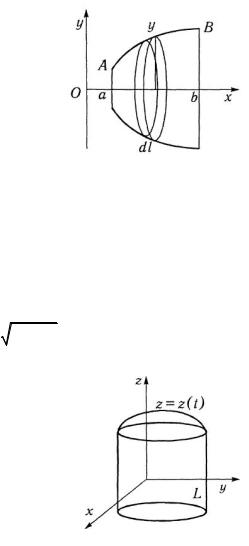
Рис. 3.37

Статические

моменты

относительно

координатных

плоскостей для цилиндрической поверхности х = x(t), у = y(t)

с

образующими

параллельными

осиz (рис.

3.38) и

ограниченной сверху кривой z = z(t) находятся по формулам

ò

ò

2

ò

myz =

xzdl; mzx =

yzdl;

mxy =

1

z2dl,

(7)

L

L

L

где

dl = x&2 + y&2 dt;

L – проекция

поверхности на

плоскость

xOy.

i=1

Моменты

инерции

относительно

координатных

осей

плоской

кривой y = f (x) (a £ x £ b)

вычисляются

по

формулам

x

b

( )

2

b

( )

2

(

2

òa

òa

¢

)

I = d x y dl = d x y 1+

y

dx,

(8)

b

( )

2

b

( )

2

(

2

y

òa

òa

¢

)

I = d x x dl = d x x 1+

y

dx,

где d (x) - плотность,

dl - дифференциал дуги.

Моменты

инерции

криволинейной

,

трапе

ограниченной кривой y = f (x),

осью Ox

и двумя

прямыми

x = a и x = b вычисляются по формулам

I x

=

1

òab d (M )y 3 dx ; I y

= òab d (M x)2 ydx .

(9)

3

Моменты

инерции

плоской

фигуры(рис. 3.39),

ограниченной

кривыми y1

= f1 (x), y2 = f 2 (x),

относительно

осей координат вычисляются по формулам

относительно

оси Ox

дуги:

а) кривой

y = e x (0 £ x £ 1);

б) астроиды

x

23 + y

23

= a

2 3 ,

лежащей

в

первом

квадрате,

d (x) = 1 ; в) окружности x 2

+ y 2

= a 2 , расположенной в первом

квадранте,

если

в

каждой

её

точке

плот

пропорциональна произведению координат точки.

Решение.

а) статический

момент

относительно

осиOx

mx = ò01 e x 1 + e2 x dx

Делая замену t = e x ,

dt = ex dx , получим mx = ò1e

1+ t 2 dt .

Интегрируя

по

частям: u =

1 + t 2 ,

dv = dt ;

du =

tdt

,

t = v , будем иметь

1 + t 2

dt

mx = t 1+ t 2 -

e

1+ t 2 dt +

e

,

ò1

ò1

1+ t2

mx = ò1e

1+ t 2 dt =

1

(t 1+ t2 + ln (t + 1+ t2 ))

1e

=

2

1

æ

e +

1 + e

2

ö

=

ç

e

1 + e

2

-

2 + ln

÷

ç

.

2

1 +

2

÷

è

ø

I

1 e2 x 1+ e2x dx =

1

1

1+ e2 x

)

1

d 1+ e2 x

)

=

2

=

x

ò0

ò0

2

(

(

1

2x

3

1

1

æ

2

3

ö

2

2

=

(1+ e

)

=

ç(1+ e

)

- 2 2

÷.

3

0 3 è

ø

б) Запишем уравнение астроиды в параметрическом виде

x = a cos3 t ,

y = a sin 3 t .

При нахождении статического момента относительно оси

Ox

воспользуемся

формулами(1),

для

этого

вычислим

дифференциал дуги

dl =

x&2 + y&2 dt = 3a

cos4 t sin2 t + sin4 t cos2 tdt =

= 3a sin t cos t dt ,

p

p

3a

2

p

3

2

mx = ò0

2 ydl = 3a2 ò0

2 sin3 t sin t cos tdt =

sin5 t

=

a2 .

0

2

5

Момент инерции по формулам (8) равен

p

p

3a

3

p

3

2

I x

= ò0

2 y 2 dl = 3a3 ò0

2 sin 6 t sin t cos tdt =

sin 8

t

=

a 3 .

0

8

8

Следует

заметить,

что

в

силу

симметрии

астроиды

относительно координатных осей mx = my

=

3

a 2 и

3

5

I x

= I y

=

a 3 .

8

в) Статический момент и момент инерции находим по

формулам (1) и (8).

Дифференциал дуги

равен dl

=

1 + (y )2 dx

,

где y¢

находим

из

дифференцирования

уравнения

окружности

dl = 1 + x 2

dx = 1

y 2 + x 2 dx = a dx .

y 2

y

y

Таким образом,

a

mx = ò0a kxy × y

dx = kaò0a x

a2 - x2 dx =

y

= -

ka

ò0a

(a2 - x2 )12 d (a2 - x2 )=

2

= -

ka

(a 2 - x 2 )3 2

a

=

ka 4

.

3

0

3

I x

= ò0a kxy × y 2

a

dx = kaò0a xy 2 dx = kaò0a x(a 2 - x 2 )dx =

y

æ

2

x 2

x 4 ö

a

ka

5

ç

÷

.

= kaça

-

÷

=

2

4

è

4 ø

0

Здесь k

- коэффициент пропорциональности.

6.2. Найти статический момент и момент инерции

полуокружности радиуса a относительно её диаметра.

Решение.

Расположим

декартову

систему

координат

таким образом, чтобы ось Ox

совпала

с диметром, а начало

координат с центром окружности. В этом случае уравнение

окружности

в

параметрической

форме

примет:

ви

x = a cos t, y = a sin t .

Тогда

дифференциал

дуги

dl = a 2 sin 2 t + a 2 cos2 tdt = adt .

Воспользовавшись

формулами (1) и (8), получим

mx

= ò0p

ydl = a 2 ò0p sin tdt = 2a 2 ,

I x

=

p

y 2 dl = a3

p sin 2 tdt =

1

pa3 .

ò0

ò0

2

r 2 + r¢2 = 4a 2 sin 2 j + 4a 2 cos2 j = 2a(0 £ j £ p )

(рис.

mx

= 4a 2 ò0p sin 2 jdj = 2a 2 ò0p (1 - cos 2j)dj = 2pa 2 ;

my

= 4a 2 ò0p sin j cosjdj = 0 .

То, что my

= 0 и следовало ожидать,

так как дуга окружности

симметрична относительно оси Oy .

6.4. Найти статические моменты и моменты инерции

прямоугольника

со

сторонамиa

и b

относительно его

сторон.

Решение. Расположим оси координат так, как показано на

рис. 3.41.

Воспользуемся

формулами (3),

(9),

полагая плотность

равной единице. Будем иметь:

1

a

2

1 a

2

1

2

ma

=

y

dx =

b

dx =

ab

,

2

2

ò0

2 ò0

1

mb

= ò0a xydx = ò0a bxdx =

a 2b ,

1

1 a

2

1

a

3

3

3

I a =

y

dx =

b

dx =

ab

,

3

3

ò0

3 ò0

Ib

= ò0a x 2 ydx = ò0a x 2bdx =

1

a3b .

3

треугольника,

ограниченного

линиями x = 0 ,

y = 0 и

x + y = a ; а)

относительно координатных осей; б)

прямой,

1

æ

2

2

x3

ö

a

a3

=

ç a

x - ax

+

÷

=

;

2

3

6

è

ø

0

1

a

3

1 a

3

1 (a - x)4

a

a 4

I x

=

y

dx =

(a - x)

dx = -

=

.

3

3 ò0

3

4

0

12

ò0

В силу симметрии mx

= my

=

a 4

и I x = I y

=

a 4

.

6

12

на расстоянии h

от вершины треугольника. Из подобия

треугольников

a y

=

h

и ay = h . Отсюда, статический момент

a

a

и момент инерции

ml

= ò0a a y hdh = ò0a h 2 dh =

a 3

;

3

Il

= ò0a a y h 2 dh = ò0a h3dh =

h 4

.

4

расстоянии

h

от неё.

Ширина сечения выше осиl

равна

ay =

2

a - h , ниже ay =

2

a + h .

3

3

Поскольку

ось l

проходит через центр тяжес, тои

статический

момент

треугольника относительно

оси равен

2

æ 2

ö

æ

2

h

2

h

3

ö

2

a

a

3

4

a

3

â

3

ç

÷

ml

ç

a

-

=

,

= ò0

3

a - h ÷hdh = ç

3

2

3

÷

0

27 3

è

ø

è

ø

для нижней

a

æ 2

ö

æ

2