
Учебное пособие 1733
.pdfn
u = lim å f (xk )Dxk .
Dxk ®0 k =1
В предложенной схеме определенный интеграл рассматривается как предел интегральной суммы.
2°. Некоторые величины целесообразнее вычислять посредством определенного интеграла, пользуясь другой схемой.
а) Пусть некоторая часть искомой величины и есть неизве-
стная функция Du |
от |
переменной x , |
которая изменяется в |
|||
известном из условия задачи интервале x Î[a,b] . |
|
|
||||
б) Представим дифференциал функции du в виде произве- |
||||||
дения du = f (x )dx , где f(x) - заданная из условия задачи фун- |
||||||
кция от х. |
|
дифференциал функцииdu при |
|
|
||
в) Поскольку |
dx ® 0 |
и |
||||
приращение |
Du |
есть |
бесконечно |
малые величины |
одного |
|
порядка |
малости, то |
искомая |
величина |
находится |
||
интегрированием du в пределах от x = a до x = b , т.е. |
|
|||||
|
|
|
b |
|
|
|
u = ò f (x )dx
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.1. Найти площадь криволинейного треугольника, ограни- |
|
|||||||||||||||||||||
ченного |
параболой y = x2 , осью |
Ox |
и прямой x = 1 :а) |
|
рас- |
|
|||||||||||||||||
сматривая определенный интеграл как предел интегральной |
|
||||||||||||||||||||||
суммы; б) посредством дифференциала искомой площади. |
|
|
|||||||||||||||||||||
|
Решение. а) Разобьем отрезок интегрирования[0,1] на п |
|
|||||||||||||||||||||
равных |
|
n -1 |
частей |
|
точками |
|
|
деления |
|
с |
абсц |
||||||||||||
0, |
1 |
, |
2 |
,..., |
,1 и |
выберем |
|
из |
полученныхчастичных |
|
|||||||||||||
n |
|
|
|
|
|
||||||||||||||||||
|
|
n |
|
n |
|
|
1 |
|
|
2 |
|
|
|
n -1 |
|
|
|
|
|||||
отрезков правые концы, |
т.е. x = |
, x |
= |
,..., x |
n-1 |
= |
, x |
n |
=1 . |
|
|||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
2 |
|
n |
|
n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Длина |
каждого |
из |
этих |
|
частичных |
|
промежутков |
равна |
|||||||||||||||
Dx |
= |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
k |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
101
Так как y = x2 , то
f (x |
)= æ |
1 |
ö2 |
, f (x |
|
|
)= |
æ 2 ö2 |
,..., f (x |
|
)= |
æ n ö2 |
|||||||||||||||||||||||||||||||||||||
|
|
2 |
ç |
|
|
|
÷ |
|
|
n |
ç |
|
÷ |
||||||||||||||||||||||||||||||||||||
1 |
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
è n |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è n ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è n |
ø |
||||||||||||
и приближенное значение каждого элемента DSk |
выразится в |
||||||||||||||||||||||||||||||||||||||||||||||||
виде произведения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
DSk = |
æ k ö2 1 |
|
|
|
|
k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
ç |
|
|
|
|
÷ |
|
|
|
|
|
|
= |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
n |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
è n ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Составим сумму таких произведений |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
n |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Sn = åDSk |
= å |
k |
= |
|
|
(12 + 22 + 32 + ... + n2 ). |
|||||||||||||||||||||||||||||||||||||||||||
3 |
|
n |
|||||||||||||||||||||||||||||||||||||||||||||||
|
k =1 |
|
|
|
|
|
k =1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пользуясь формулой суммы квадратов целых чисел |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
å k 2 = n ( n + 1 )( 2 n + 1 ) , |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
находим |
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn |
= |
1 |
æ |
|
n |
3 |
+ |
n |
2 |
|
+ |
n |
ö |
= |
1 |
+ |
1 |
+ |
1 |
|
. |
|
|
|
|||||||||||||||||||||||||
|
ç |
|
|
|
|
÷ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
n |
è |
|
3 2 6 |
ø |
|
|
|
|
3 2n 6n |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Искомая площадь |
|
определяется |
|
|
|
|
пределом |
|
приDxk ® 0 , |
||||||||||||||||||||||||||||||||||||||||
т.е. при n ® ¥ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
S = lim ç |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
÷ |
= |
|
|
|
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
n®¥ è |
|
3 2n 6n |
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
б) Для криволинейного треугольника, прилежащего к оси Ox (рис. 3.1) дифференциал переменной площади S (x) = SOMx
есть площадь прямоугольника со |
|
сторонамиy и dx, т.е. |
||||||
dS = ydx . |
|
|
|
|||||
Подставляя сюда значение функции и интегрируя в задан- |
||||||||
ных пределах a = 0 , b =1, получим |
|
|
|
|||||
S = ò01 x2dx = |
x3 |
|
|
1 |
= |
1 |
. |
|
|
||||||||
|
|
|||||||
3 |
|
0 |
3 |
|||||
|
|
|
|
|||||
102

Рис.3.1
3.2. Площадь плоской фигуры
Площадь всякой плоской фигуры в декартовой системе координат может быть составлена из площадей криволинейных трапеций, прилежащих к оси Ox или Oy .
1°. Площадь криволинейной трапеции aABb (рис. 3.2), прилежащей к оси Ox находится по формуле
S = òab |
f (x )dx = òab ydx . |
(1) |
2°. Площадь криволинейной трапеции cCDd (рис. 3.3), |
||
прилежащей к оси Oy находится по формуле |
|
|
S = òcd j ( y )dy = òcd xdy . |
(2) |
|
|
Рис.3.2 |
Рис.3.3 |
|
3°. Если фигура образована пересечением кривых так, что |
|||
любая прямая, параллельная оси Oy , пересекает ее границы |
|||
не более чем в двух точках(рис. 3.4), то ее площадь равна |
|||
разности |
площадей |
соответствующих |
криволинейных |
трапеций и определяется по формуле
103

S = |
b |
( |
f |
2 |
( |
x - f |
( |
x |
dx = |
b |
( |
y |
2 |
- y |
dx . |
(3) |
|
|
òa |
|
) |
1 |
|
)) |
òa |
|
1 ) |
|
|
||||||
Рис.3.4 |
Рис.3.5 |
Если фигура образована пересечением кривых так, что лю- |
|
бая прямая, |
параллельная оси Ox , пересекает ее границы не |
||||||||||||||
более, чем |
|
в двух точках (рис. 3.5), то ее площадь |
|||||||||||||
определяется по формуле |
|
|
)) |
|
|
|
|
|
|
|
|||||
S = |
d |
j |
2 ( |
y -j |
y |
dx = |
d |
x |
2 |
- x |
dy . |
(4) |
|||
|
|
òc ( |
|
) |
1 ( |
|
|
òc ( |
|
1 ) |
|
|
|||
4°. Площадь всякой плоской фигуры в полярной системе координат может быть составлена из пло криволинейных секторов.
Площадь криволинейного сектора ОАВ (рис. 3.6) находится по формуле
S= 1 òj2 r2dj . 2 j1
Рис.3.6
104
5°. Площадь криволинейной трапеции, ограниченной кривой, заданной в параметрической форме x = j (t ); y =y (t ) , где
t Î[a, b ] и j (a ) = a;j (b ) = b , определяется по формуле
S = òab ydx = òaby (t )j¢ t( dt) . |
(6) |
2.1. Найти площадь фигуры, ограниченной линиями:
а) y = x + 2, y2 = 9x; б) xy =1, y = x, x = 4, y = 0; в) x = 1 y2 ,
|
|
|
2 |
|
осью ординат и прямыми y =1, y = -3 ; г) y = x2 , y2 = -x ; |
||||
д) y = x2 |
, y = x3 |
- |
x2 |
|
, x = ±1; е) y = xe 2 и ее асимптотой; |
||||
ж) y2 = x (x - a )2 .
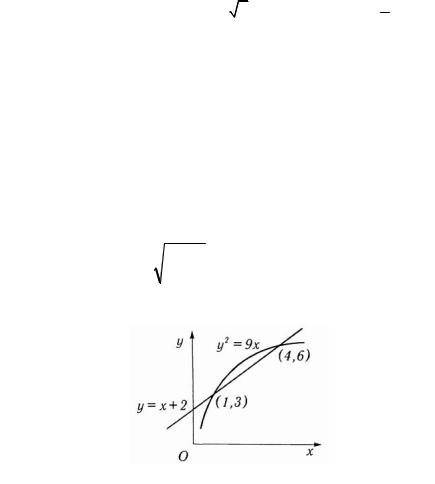
Решение. а) Построим графики (рис. 3.7) и найдем точки пересечения этих линий. Для этого решим систему
|
|
|
|
|
|
|
ìy = x + 2; |
|
|
||||
|
|
|
|
|
í |
= 9x. |
|
|
|||||
|
|
|
|
|
|
|
îy2 |
|
|
||||
Откуда |
(x + 2)2 |
= 9x |
|
или x2 - 5x + 4 = 0 . Точки |
|||||||||
пересечения x |
|
= |
5 |
± |
|
25 |
- 4 = |
5 |
± |
3 |
; x |
= 4; x = 1 . |
|
|
|
|
|
|
|||||||||
1,2 |
2 |
|
4 |
|
2 |
|
2 |
|
1 |
2 |
|||
|
|
|
|
|
|
|
|
||||||
Применяя формулу (3) будем иметь
Рис.3.7
105

|
4 |
|
|
|
|
4 |
4 |
æ |
2 |
3 |
æ x2 |
öö |
|
4 |
|||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
S = ò1 ëé |
9x -(x +2)ûùdx =3ò1 |
xdx -ò1 |
(x +2)dx = ç3 |
|
x 2 |
-ç |
|
+2x ÷÷ |
|
= |
|||||||||||||
3 |
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
è |
øø |
|
1 |
|||||
æ |
|
3 |
|
2 |
ö |
|
4 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
=ç |
2x2 - |
x |
-2x÷ |
|
= 2×8-8-8-2+ |
1 |
+2 = |
1 |
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
è |
|
|
|
2 |
ø |
|
1 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
б) Построим графики (рис. 3.8) и найдем координаты точки A пересечения гиперболы и параболы, решая их уравнения совместно; A(1,1). Поскольку криволинейная трапеция сверху ограничена различными кривыми, то разбивая промежуток интегрирования на два промежутка и пользуясь формулой (1), получим
1 |
4 dx |
|
2 |
3 |
|
|
1 |
|
|
|
|
4 |
|
2 |
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
S = ò0 |
xdx + ò1 |
|
= |
|
x 2 |
|
|
|
+ ln |
x |
|
|
|
= |
|
+ ln 4 |
- ln1 = |
|
+ 2ln 2 . |
|
x |
3 |
|
|
0 |
|
|
1 |
3 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3.8
в) Площадь криволинейной трапеции ABCD (рис. 3.9) находим по формуле (2)
S = |
1 |
ò-13 y2dy = |
1 |
y3 |
1 |
1 |
(1+ 27) = |
14 |
|
|
= |
. |
|||||||||
|
|
|
|
|||||||
2 |
6 |
|
-3 |
6 |
3 |
|
||||
106

Рис.3.9
г) Построим графики (рис. 3.10) и из решения системы: y = x2 , y2 = -x найдем точки пересечения этих линий (0,0), (-1,1). Применяя формулу (3), получим
0 |
|
æ |
|
2 |
|
2 |
|
x |
3 |
ö |
|
0 |
|
2 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||
S = ò-1 |
( |
(-x) - x2 )dx = ç |
- |
(-x 3) - |
|
÷ |
|
|
= |
- |
= |
. |
|||||||
3 |
|
|
|
|
|
||||||||||||||
|
|
è |
|
|
|
3 |
ø |
|
-1 |
3 3 3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис.3.10
д) Сделаем чертеж (рис. 3.11). Пределы интегрирования даны по условию. Искомая площадь будет
1 |
|
æ |
x |
3 |
|
x |
4 |
ö |
|
1 |
|
2 |
|
|
|
|
|
|
|||||||||
S = ò-1 |
(x2 |
- x3 )dx = ç |
|
- |
|
÷ |
|
|
= |
. |
|||
3 |
|
|
|
|
|
||||||||
|
|
è |
4 |
ø |
|
-1 |
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
107

Рис.3.11
е) Функция нечетная, следовательно, ее график симметричен относительно начала координат. Найдем ее асимптоту
y = kx + b : k = lim |
y |
= lim e- |
x2 |
= 0, b = lim y = lim |
x |
= 0 , |
||||
2 |
||||||||||
|
2 |
|||||||||
x®¥ x |
x®¥ |
|
x®¥ |
x®¥ |
|
x |
|
|||
|
e 2 |
|||||||||
|
|
|
|
|
|
|||||
таким образом, асимптотой будет прямая y = 0, т.е. ось Ox
(Рис.3.12)
|
|
|
|
|
Рис.3.12 |
|
|
|
|
|
|
|
|
|
|
Вследствие |
симметрии, достаточно |
|
найти |
половину |
|||||||||||
площади |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
¥ |
- |
x2 |
|
b - |
x2 |
|
æ |
|
x |
2 |
ö |
|
|
|
S = ò0 |
xe 2 dx = - blim®¥ |
ò0 e 2 d ç |
- |
|
÷ |
= |
|
|||||||
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
è |
2 |
ø |
|
|
||||
= - lim e |
- |
x2 |
|
|
b |
|
æ |
- |
b2 |
ö |
|
|
|
||||||||
2 |
|
|
|
= - lim çe |
2 |
-1÷ =1, S = 2. |
||||
b ®¥ |
|
|
|
|
|
b ®¥ |
ç |
|
|
÷ |
|
|
|
0 |
|
è |
|
|
ø |
||
|
|
|
|
|
||||||
108

ж) Функция четная относительно переменнойу, следовательно, фигура, ограниченная заданной кривой, симметрична относительно оси Ox (рис. 3.13).
Рис.3.13
Найдем точки пересечения с осьюOx . Полагая y = 0 , будем иметь x = 0, x = a , следовательно, x изменяется от 0 до
а.
Половину площади найдем по формуле (1)
1 |
a |
a æ |
3 |
1 |
ö |
|||
|
|
|
||||||
S = ò0 |
x (x - a)dx = ò0 |
çx 2 -ax 2 |
÷dx |
|||||
|
||||||||
2 |
|
è |
|
|
|
ø |
||
æ 2 |
|
5 |
|
2 |
|
3 |
ö |
|
a |
4 |
|
|||||
|
|
|
||||||||||||||
x 2 - |
ax 2 |
a a . |
||||||||||||||
= ç |
|
|
|
|
÷ |
|
= - |
|
|
|||||||
5 |
3 |
|
15 |
|||||||||||||
è |
|
|
|
|
|
ø |
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Знак минус означает, что фигура расположена ниже оси Ox . Это, кстати, следует даже из того, что подынтегральная
функция |
на |
промежутке |
интегрирования |
|
отрицательна |
||||||||
x (x - a) £ 0 |
при x Î[0, a] . Следовательно, |
найденный |
|||||||||||
результат надо взять с противоположным знаком. Таким |
|||||||||||||
образом, вся площадь будет равна S = |
8 |
a a . |
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||
2.2. Найти |
|
|
|
|
|
15 |
|
|
|
|
|
|
|
площадь, |
ограниченную: |
а) |
эллипсом |
||||||||||
x = a cos t, y = b sin t ; |
б) |
одной |
|
|
|
аркой |
|
|
циклоиды |
||||
x = a (t - sin t ), y = a (1- cos t ) |
и |
( |
|
осьюx; |
в) |
астроидой |
|||||||
x = acos3 t |
y = sin3 t ; г) кривой x = 2 |
t2 |
) |
( |
4 |
-t 2 |
) |
. |
|||||
|
-1 , y = t |
|
|
||||||||||
Решение. а) Оси координат делят эллипс на четыре одинаковые части. Найдем площадь, расположенную в первом квадранте
1 S = òa ydx .
4 0
109

Поскольку эллипс задан уравнениями в параметрическом виде, то преобразуем интеграл к переменной t. При x =0, t =p ,
а при x = a, t = 0 . Таким образом |
|
|
|
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
1 |
|
|
p |
||
0 |
|
|
|
|
2 |
|
|
|
|
|
|
æ |
ö |
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
S = -4ò |
p |
absin |
|
t dt = 2abò02 (1-cos 2t )dt = 2ab çt - |
|
sin 2t ÷ |
|
|
= pab. |
||||||||||||
|
2 |
||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
ø |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) При x = 0,t = 0 ; при y = 0,t = 2p . По формуле (6) имеем |
|||||||||||||||||||||
S = ò02p a2 (1- cos t )2 dt = a2 ò02p (1- 2 cost + cos2 t )dt = |
|||||||||||||||||||||
|
|
|
2 |
æ |
3 |
|
|
|
1 |
|
ö |
|
2p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= a |
|
ç |
|
t |
- 2sin t + |
|
|
|
sin 2t ÷ |
|
|
= 3pa |
. |
|
|
|
|
|
|||
|
2 |
4 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
è |
|
|
|
|
ø |
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
в) Оси координат делят астроиду на четыре одинаковые части. Найдем площадь, расположенную в первом квадранте.
При |
x = 0, t = |
p |
; |
при |
|
y = 0,t = 0 . Отсюда по формуле (6) |
|
вся |
|||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
площадь будет равна |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
0 3a2 sin3 t cos2 t sin tdt = |
3 |
|
|
|
|
|
|
|
|
) |
|
|
||||||||||||||||||||
S = -4 |
|
a2 |
|
2 |
1-cos 2t -cos2 |
2t +cos3 2t |
dt = |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
ò0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3 |
|
|
éæ |
|
|
1 |
|
|
|
|
|
|
|
ö |
p |
|
|
1 |
p |
|
|
|
1 |
p |
|
|
ù |
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò02 (1-sin |
2t )d sin 2t ú |
|
||||||||||||||||
= |
|
|
a |
|
êçt - |
|
|
sin 2t |
÷ |
|
- |
|
ò02 (1-cos 4t )dt + |
|
|
= |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
2 |
|
|
êè |
|
|
2 |
|
|
|
|
|
|
ø |
0 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
ú |
|
|||||
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
||
|
3 |
|
2 |
æp |
|
p ö |
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
|
|
a |
|
ç |
|
|
- |
|
|
÷ |
= |
|
|
|
pa |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
2 |
4 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
г) Найдем точки пересечения кривой с осями координат. Если x = 0 , то t = ±1; если y = 0 , то t = 0, t = ±2 . Отсюда получим следующие точки:
при t = -1 (0, -3), при t = 1 (0,3); при t = 0 (0, -2) ;
при t = ±2 (6,0).
110
