Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1733

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2413 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

								1		3								3 x	2	1		æ	x	3	ö	1
			b	y2dx = p				1						1			(1- x2 )dx = p		2		2	æ		3	ö	1
V = p							2				xdx +p 1											+p çx -			÷	=
V = p							2				xdx +p 1											+p çx -			÷	=
		òa					ò0		2					ò				2 2				è	3		ø	1
		òa					ò0		2					ò	2			2 2			0	è	3		ø	1
æ 3 1				+1-	1		1				1	ö		19		p.										2
æ 3 1					1		1				1	ö		19
= p ç						-			+			÷	=
= p ç	2 8				3	-	2		+		24	÷	=	48
è	2 8				3		2				24	ø		48

3.7. Доказать, что объем параболоида вращения равен половине объема кругового цилиндра, имеющего то же основание и ту же высоту.

Решение. Считаем, что параболоид образован вращением параболы y2 = 2 px вокруг оси Ox , причем сечение возьмем в

произвольной точке с	абсциссойx	(рис. 3.25). Тогда его
объем равен
x			x
Vn = p ò0	2 pxdx = p p x2		0	= p px2 .
Vn = p ò0			0

Рис.3.25

Объем цилиндра, имеющего то же основание и ту же высо-

ту, равен V = p y2 x . Поскольку y2 = 2 px , то V = 2p px2 .
ö	ö
Сравнивая	результаты, получим Vö = 2Vn , что и

требовалось доказать.

3.8. Найти объем тела, образованного вращением фигуры, ограниченной линиями: y = cos x и y = -1 вокруг прямой y = -1 при -p £ x £ p

Решение. Тело, образованное вращением фигуры, ограниченной заданными линиями, показано на рис. 3.26.

121

Рис.3.26

Поскольку кривая вращается вокруг прямойy = -1, то

целесообразно				перейти к новой			системе координат
x¢ = x; y¢ = y +1. Тогда объем тела вращения равен
V = p ò-pp (y¢ )2 dx¢ = p ò-pp (y +1)dx = p ò-pp (cos x +1)2 dx =
p	æ	3		ö	3		p	2


= p ò-p	ç		+ cos 2x + 2 cos x ÷ dx = p			x	= 3p		.
		2			2
	è			ø			-p

3.9. Найти объем тела, образованного вращением вокруг полярной оси: а) кардиоиды r = a (1- cosj ); б) лемнискаты r2 = a2 cos 2j .

Решение. а) Очевидно, что j изменяется от 0 до p . Отсюда по формуле (6) имеем

			2		p	3	(1	- cosj )			3			2		3	p	(1- cosj )	3	d 1(- cosj ) =
V =				p	ò0 a							sinjdj =			pa		ò0
V =			3	p	ò0 a							sinjdj =		3	pa		ò0
	1		3									8		3
=		pa3			(1- cosj )4				p	=			p a3 .
									p

6									0		3
6									0		3

б) Так как лемниската симметрична относительно начала координат, то половина объема по формуле (6) равна

1		2		p		3			2		p	3
	V =					(cos 2j )				p a3		(2 cos2 j -1)
			p ò04		a3			sin jdj =			ò04		2	sin jdj .
							2
2									3
	3

122

Сделаем

замену:

cosj =

,sin jdj =

cos tdt

; при

2 sin t

2 sin 2 t

j = 0, t =

; при j =

, t =

, тогда

p3 cos4 tdt

V =

- 2 + sin

t ÷dt =

sin2 t

ò4

è sin2 t

1 æ

öö

-ctgt - 2t +

çt -

sin 2t ÷

p a

5 -

÷.

3 2

2 è

3.10. Найти объем тела, образованного вращением: а) од-

ной ветви циклоиды x = a (t - sin t ), y = a (1- cos t )

вокруг оси

Ох; б) фигуры, ограниченной кривой x = 3t2 , y = 2 ln t и осями

координат,	вокруг	координатных	;осейв) астроиды
x = a cos3 t ,	y = a sin3 t вокруг прямой x = a .

Решение. а) Одна ветвь циклоиды получается при измене-

нии t от 0 до 2p , а x от 0 до 2p a . Следовательно, искомый

объем равен

V = p ò02p a y2dx .

Используя

параметрические

уравнения

циклоиды,

получим

- cos t )

2p æ

+cos 2t )-

V = pa

ò0

dt = p a

ò0

ç1-cos t +

2 3

-(1-sin

t )cos t )dt = pa

t -

4sin t +

sin 2t +

sin

t ÷

=5p

a .

б) Фигура, ограниченная заданной кривой и осями координат, показана на рис. 3.27, где t Î[0,1]. Объем тела вращения вокруг оси Ox находим по формуле

3 1

V = p ò0 y2dx или V = 24p ò0 t ln2 tdt .

123

Рис.3.27

При t = 0 подынтегральная функция терпит разрыв. Интегрируя несобственный интеграл дважды по частям: ln2 t = u ,

ln tdt

= du; tdt

= dv, v =

, получим

V = 24p lim

2 t

òb

t ln tdt ÷

= 24p ç- lim

÷ +

b ®0

è 2

ç b ®0

ln b

ln t +

+ lim

= 24p ç-lim

+ lim

ln b +

÷ =

b ®0

ç b ®0

b ®0 2

4 ÷

æö

ç	ln b				1	÷
= 24p çlim				+		÷ = 6p.
= 24p çlim	1			+	4	÷ = 6p.
ç b ®0	1				4	÷
ç		b	2			÷
è		b				ø

Объем тела вращения вокруг оси Oy находим по формуле

(3). При y = -¥,t = 0 ; при y = 0,t =1, отсюда

V = p ò-0¥ x2dy = 9p ò01 t4	dt		9	pt 4	1	9	p .

		=			=

	t 4				0	4

в) Поскольку астроида симметрична относительно оси Ox , то достаточно найти половину объема тела вращения. Так как

124

астроида вращается вокруг прямой x = a , то перенесем начало координат в точку (a, 0) , тогда в новой системе координат x¢ = x - a, y¢ = y формула для вычисления объема примет вид

1V = p òa (x¢ )2 dy¢ = p òa (x - a )2 dy .

20 0

Рассматривая только объем тела, получающийся от вращения вокруг прямой x = a фигуры, ограниченной верхними ветвями астроиды, и переходя к переменной t , представим его как разность интегралов

V = 6p a 3

òp2 (cos3 t -1)

sin 2 t cos tdt - ò02 (cos3 t -1)

sin 2

t cos tdt ÷

= 6p a3 çæ

òp2 (2 - 3 sin 2 t + 3 sin 4 t - sin 6 t )sin 2 td sin t - 2 òp2

cos 4 t sin 2 tdt -

- ò02 (2 -

t )sin 2

td sin t + 2 òp2 cos 4

3 sin 2 t + 3 sin 4 t - sin 6

t sin 2

tdt ÷

æ 2

6p a

(ç

sin

t -

sin

t +

sin

t -

sin

t ÷

òp2

+ cos 2t -

+ cos 4t )- (1 - sin

2t )cos 2t ÷dt

sin

t -

sin

t +

sin

t -

sin

t ÷

ò02

ç1

+ cos 2t -

+ cos 4t )- (1 - sin

2t )cos 2t ÷dt) =

		æ 2			3		3		1 ö			1		p	æ	2		3		3		1 ö			1
= 6p a	3												t	2												t
		(ç		-		+		-		÷	-				- ç		-		+		-		÷	+
			3		5		7		9			8				3		5		7		9			8
		è								ø				p	è								ø

	2	= 3 p 2 a3 .
	2

	0	4
	0	4

125

3.4. Длина дуги кривой
1°.	Если плоская	кривая отнесена к прямоугольной
системе координат и задана уравнениему = f(х) или х = F(y),
или параметрически x =φ(t), y=ψ(t), то			дифференциал dl
длины	ее дуги(рис. 3.28)	определяется,	соответственно, по

формулам
dl =	1+ ( y¢)2 dx =			1+ (x¢)2 dy =		x&2 + y&2 dt .		(1)
Интегрируя		дифференциал			дуги	в	заданных		пределах,
находим длину дуги
		b	b		b
	L = òdl = ò 1+ (y¢ )2 dy = ò					x&2 + y&2 dt .		(2)
		0	a		a
2°. Если плоская кривая отнесена к полярной системе
координат	и	задана		уравнениемr = r(j)			(рис.	3.29),	то
дифференциал		дуги	равен dl =		r 2 + (r¢ 2)dj , а длина дуги
определяется по формуле
			b	r 2 + (r¢ )2 dj .
		L = ò		r 2 + (r¢ )2 dj .				(3)

Рис. 3.28

Рис.3.29

3°. Длина дуги пространственной кривой, заданной параметрически уравнениями х = х(t), у = y(t), z = z(t) при изменении t от α до β, определяется по формуле

126

b
L = ò x&2 + y&2 + z&2 dt .	(4)
a

4.1.Найти длину дуги: а) кривой y = ln cos x от x = 0 до

x= p ; б) астроиды x2 / 3 + y 2 / 3 = a2 / 3 ; в) кривой y2 = 9 – х

между точками пересечения ее с осью Оу;

г) полукубической

параболы y 2

= x3

заключенной внутри окружности х2 +у2 =6х.

Решение.

а) Применяя формулу (1), имеем

sin 2 x

L = ò

1 +[(ln cos x) ]

dx =

1 +

cos

dx = ò

cos x

æ x

æ b

= lim ln

tgç

= lim ln tgç

= ¥

p®p

è 2 4

b ®

è 2 4

Поскольку

астроида

симметрична

относительно

координатных

осей,

то

достаточно

найти

длину одной ее

ветви.

Дифференцируя

уравнение

астроиды, имеем

y¢ = -( y / x)1/ 3 . Длина одной четверти астроиды находится по

формуле (2) и равна

x2 3 + y2 3

a 13

L =

ò 1+

(y x

dx)= ò

dx = ò

dx =

x 3

= 3 a

3 x

= 3 a

Отсюда длина всей астроиды L = 6a .

в)

Кривая

представляет

параболу

симметричную

относительно оси Ох (рис. 3.30).

127

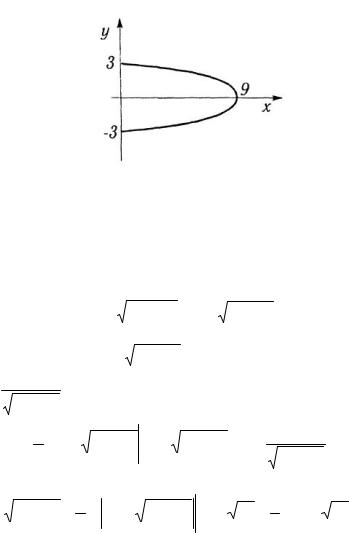
Рис. 3.30

Найдем точки пересечения с осью Оу: при x = 0, у = ±3.

Вследствие		симметрии					кривой			относительно Охоси
достаточно		найти				половину			длины		заданной . кривой
Используя формулу (1), будем иметь
		1		3				3
		1	L = ò 1 + (x¢ )2 dy = ò 1 + 4 y 2 dy .
		2	L = ò 1 + (x¢ )2 dy = ò 1 + 4 y 2 dy .
		2		0				0
				0				0
Интегрируя по частям					1+ 4 y 2		= u , dy = dv;
du = 4 ydy	,	u = y , получим
1+ 4 y 2
1 L = y 1 + 4 y					2	3			3	dy	2 .
1 L = y 1 + 4 y					2	- ò 1 + 4 y 2 dy + ò				dy	2 .
					3
2					0	0			0	1+ 4 y
Отсюда								= 3 37 + 1 ln(6 + 37 ).
L = y 1+ 4 y 2 + 1 ln 2 y + 1+ 4 y 2								= 3 37 + 1 ln(6 + 37 ).
							3
		2					0			2

г) Сделаем чертеж (рис. 3.31) и найдем точки пересечения окружности и параболы.

Для этого решим системуу2 =х3, х2 —6х + у2 =0. Абсциссы точек пересечения будут 0 и 2.

Вследствие симметрии достаточно найти половину длины дуги. По формуле (1) имеем

128

Рис 3.31

1	2
1	L = ò
2	0

Таким образом

1 +

æ 3

dx =

ç1

8 æ

ö3

çæ

11 ö2

ç1 +

x ÷

æ 11 ö

L =

-1÷ .

2 ø

1		æ 9
ö				ö
ö	2			ö
÷		dç		x ÷	=
÷		dç	4	x ÷	=
ø		è	4	ø
		ö
-		÷
-		1÷
		÷
		ø

4.2.Найти длину дуги кривой: а) x = a(cos t + tsint),

у= a(sint - tcost) от точки t1 = 0 до точки t2 = 2π; б) одной арки

циклоиды x = a(t - sint), y = a(1- cost); в) x =		t 6	,	y = 2 -	t 4
		6			4

между точками пересечения с осями координат.
Решение. а) Заданная кривая	представляет эвольвенту
(развертку) окружности (рис. 3.32). Находим			производные
x& = atcost, y& = atsint. Длина дуги	кривой			находится по
формуле (2)

129

Рис 3.32

2													2p							2		2p	= 2ap 2 .
L = ò	a2t 2 cos2 t + a 2t 2 sin 2 tdt = a òtdt = at																						= 2ap 2 .
0												0							2		0
6) Здесь t изменяется									от 0 до 2π. Находим														производные
x& = a (1- cos t ),			y& = a sin t .						Длина		одной								арки				циклоиды по
формуле (2) равна
2p																		2p
L = ò		a2 (1- cos t)2 + a2 sin 2 tdt = a														2 ò			1- cos tdt =
0																0
			2p			t								t				2p = 8a.
			2p
			= 2a ò sin					dt = -4a cos
			= 2a ò sin					dt = -4a cos
			0	2								2						0
			0	2								2						0
в) Найдем пределы интегрирования: при x = 0, t = 0; при
y=0, t = 4	8	.	Вычисляя							производные x& = t 3 ,													y& = -t 3 и
используя формулу (2), находим
4 8				4 8								4 8									1
L = ò t10 + t6 dt = ò t3 t 4 +1dt =												1			ò (t 4 +1)							d	(t 4 +1)
												1									2
												4									2
0				0								4				0
				1					4	3	4 8	13
										3	4 8
			=				(t			+1)2	0 =						.
			=		6		(t			+1)2	0 =		3				.

4.3. Определить длину дуги кривой: а) первого витка спирали Архимеда r = aj ; б) кардиоиды r = a(1 +cosφ);

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2413 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.9 Mб3Учебное пособие 1729.pdf
#
30.04.2022311.71 Кб2Учебное пособие 173.pdf
#
30.04.20221.9 Mб3Учебное пособие 1730.pdf
#
30.04.20221.92 Mб8Учебное пособие 1731.pdf
#
30.04.20221.92 Mб2Учебное пособие 1732.pdf
#
30.04.20221.92 Mб4Учебное пособие 1733.pdf
#
30.04.20221.93 Mб4Учебное пособие 1734.pdf
#
30.04.20221.93 Mб4Учебное пособие 1735.pdf
#
30.04.20221.93 Mб8Учебное пособие 1736.pdf
#
30.04.20221.93 Mб12Учебное пособие 1737.pdf
#
30.04.20221.93 Mб6Учебное пособие 1738.pdf