
Учебники / Физика конденсированных сред
.pdf
§ 14. Глобальный критерий устойчивости по Ляпунову 61
Другой пример функции Ляпунова взят из области линейной неравновесной термодинамики. Здесь роль функции Ляпунова может играть производство энтропии
S˙ = i |
|
˙ |
|
|
Ii Xi ≥ 0, |
dS |
≤ 0. |
(1.98) |
|
dt |
Для систем, далеких от равновесия, также можно ввести функцию Ляпунова. Это становится особенно очевидным для систем, в которых потоки являются стационарными. Роль функции Ляпунова здесь снова может играть производство энтропии:
|
S˙ = i |
Ii Xi ≥ 0, |
|
|
|
|||||
dX S˙ |
= |
dS˙ |
= |
Ii |
dXi |
dv |
≤ |
0. |
(1.99) |
|
|
|
|
||||||||
dt |
|
dt |
|
|
i |
dt |
|
|
||
Доказательство теоремы Ляпунова для некоторых частных случаев можно найти в монографии Дж. Кайзера [13].
Можно сформулировать и другие критерии устойчивости решения дифференциальных уравнений.
Решение q(t) системы динамических уравнений (1.94) называется устойчивым (по Ляпунову), если для любых t0 и ε > 0 существует величина η = η(t0, ε) такая, что для всякого решения q (t) , удовлетворяющего в момент t0 условию
|q (t0) − q (t0)| < η, |
|
выполняется неравенство |
|
|q (t) − q (t)| < ε при t ≥ t0. |
(1.100) |
Если при t → ∞ выполняется условие |
|
|q (t) − q (t)| → 0, |
|
то можно говорить об асимптотической устойчивости решения.

62 Глава 1. Термодинамика необратимых процессов
Можно дать простую словесную интерпретацию условию (1.100). Решение (или движение) у с т о й ч и в о п о Л я - п у н о в у, если все решения (движения), находившиеся в начальный момент в непосредственной близости от него, продолжают оставаться в его окрестности. Решение (движение) асимптотически устойчиво, если все смежные решения асимптотически приближаются к нему. Устойчивость по Ляпунову накладывает весьма сильные ограничения на характер решения, так как требуется близость траекторий при всех t .
Менее строгим и более полезным при рассмотрении предельных циклов и хаотических траекторий является понятие
о р б и т а л ь н о й у с т о й ч и в о с т и. Для орбитальной устойчивости близкие в начальный момент времени траектории не обязательно должны быть близкими во все другие моменты времени. Здесь условие (1.100) заменяется более мягким: минимальное расстояние между траекториями должно быть меньше некоторого наперед заданного числа
|q (t) − q (t )| < ε при t ≥ t0, t ≥ t0. |
(1.101) |
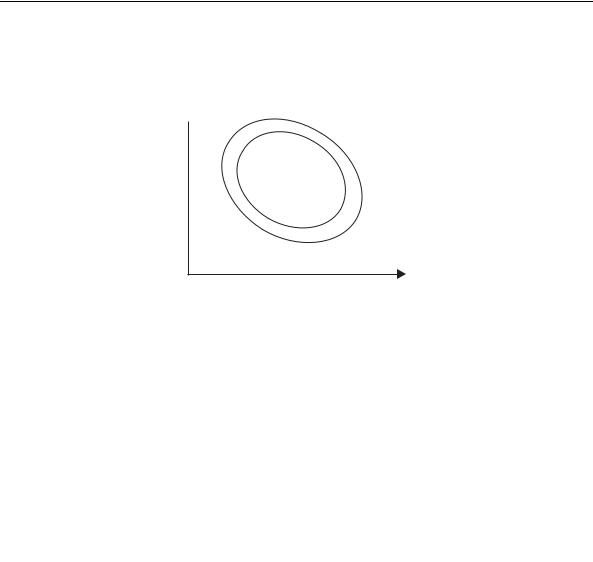
Смысл понятия орбитальной устойчивости состоит в том, что если имеются две близкие циклические траектории, то фазовые точки систем, близкие в начальный момент времени, могут сильно разойтись по истечении достаточно большого промежутка времени, например из-за разных периодов обращения. В этом случае решение не будет устойчиво по Ляпунову, но будет орбитально устойчиво (рис. 7).
Во многих физически интересных случаях, как уже указывалось, правая часть динамических уравнений (1.94) зависит от некоторого набора параметров B . Пусть bk – один из них. Если решение при изменении параметра bk на величину δbk меняется на величину |δq | δbk , то такое решение называется с т р у к т у р н о у с т о й ч и в ы м. Все значения параметров bk , при небольшом изменении которых фазовый портрет изменяется лишь количественно, будем называть обыкновенными значениями параметра. Значения параметра bk , при небольшом изменении которого имеет место качественное изменение траектории, назовем к р и т и ч е с к и м и, или
§15. Динамические системы с одной степенью свободы 63
то ч к а м и в е т в л е н и я. Точки ветвления (бифуркации) играют важную роль в процессе формирования структур при необратимых процессах.
q2 
q (t )
q (t0 )
q(t0 )
q(t )
q1
Рис. 7. К понятию орбитальной устойчивости: две фазовые точки q(t0) и q (t0) , близкие в начальный момент, сильно разошлись к моменту t , но минимальное расстояние между орбитами (показано стрелкой) осталось малым
Полный анализ структурной устойчивости динамических систем можно дать только для случаев одной или двух степеней свободы. Для произвольного числа степеней свободы исследован лишь случай градиентных систем, когда динамические уравнения движения имеют вид
dqdti = −dqdi V (q1(t), q2(t), . . . , qn(t), B) , i = 1, 2, . . . , n.
(1.102) Работы известного французского математика Р. Тома, приложившего много усилий для популяризации теории катастроф, как раз посвящены структурной устойчивости динамических
систем, которые описываются уравнениями (1.102).
§ 15. Динамические системы с одной степенью свободы
Рассмотрим случай, когда динамика системы описывается одной переменной q(t) , подчиняющейся уравнению движения
dq |
= f (q), |
(1.103) |
|
dt |
|||
|
|

64 Глава 1. Термодинамика необратимых процессов
где f (q) – некоторая функция динамической переменной q (система является автономной, поэтому правая часть уравнения (1.103) явно от времени не зависит).
Фазовое пространство в этом случае является линией, а точки стационарных состояний определяются решением уравнения f (q) = 0 .
В силу теоремы единственности, если система начала свое движение не из стационарного состояния, то она не может достигнуть его за конечный промежуток времени. В противном случае, вопреки теореме единственности, уравнение (1.103) имело бы два решения: q(t) и стационарное решение qs . Поэтому система может только асимптотически стремиться к стационарному состоянию, если оно устойчиво. Для того чтобы исследовать устойчивость системы вблизи точек стационарных состояний, разложим функцию f (q) в ряд в окрестности стационарных точек, ограничиваясь первым неисчезающим членом.
Для одномерной системы возможны лишь три ситуации, изображенные на рис. 8. Для стационарных точек q1s и q2s можно ограничиться линейными членами при разложении f (q) по q в правой части (1.103). Тогда для отклонений x(t) = q(t) − qs получаем линеаризованные уравнения
dx(t) |
= f (qs) + f (qs) x(t) + . . . . |
(1.104) |
|
dt |
|||
|
|
С учетом того, что f (qs) = 0 , вводя обозначение f (qs) = p , имеем
dx(t) |
= p x(t); x(t) = x(0) ep t, |
(1.105) |
|
dt |
|||
|
|
где x(0) – отклонение системы от стационарного состояния в момент времени t = 0 .
Из формулы (1.105) следует, что если для стационарной точки выполняется условие df /dq = p < 0 , то такая стационарная точка является асимптотически устойчивой (точка q1s на рис. 8), а если df /dq = p > 0 , то любое малое отклонение величины q от стационарного значения qs будет нарастать со
временем и система покинет окрестность стационарной точки (точка q2s ).

§ 16. Системы с двумя степенями свободы |
65 |
f (q)
p < 0 |
p > 0 |
|
p = 0 |
|
s |
s |
s |
q |
|
q1 |
||||
q2 |
q3 |
|
Рис. 8. Возможные виды стационарных точек для динамической системы с одной степенью свободы
Еще один случай, изображенный на рис. 8 (стационарная точка q3s ), также соответствует неустойчивому узлу. В этом легко убедиться, если произвести разложение f (q) до второго члена по степеням отклонений x(t) = q(t) − qs в окрестности этой точки. В итоге получаем уравнение
dx(t) |
= a x2(t), |
a = |
1 |
f (qs). |
(1.106) |
dt |
2 |
Решение уравнения (1.106) имеет вид
x(t) = |
1 |
(1.107) |
1/x(0) − a t . |
Поэтому если x(0) < 0 , то из формулы (1.107) следует, что точка q3s устойчива, а если x(0) > 0 , то стационарная точка q3s является неустойчивой. Если определять устойчивость по Ляпунову (1.96), то следует классифицировать эту стационарную точку как неустойчивую.
§ 16. Динамические системы с двумя степенями свободы
Перейдем теперь к качественному анализу поведения автономных систем с двумя степенями свободы вблизи стационарных точек. Пусть динамика системы описывается двумя пере-

66 Глава 1. Термодинамика необратимых процессов
менными q1 и q2 , временная зависимость которых определяется уравнениями
dq1 |
= f |
1 |
(q , q ), |
|
|||
|
|
|
|
||||
|
dt |
|
1 |
2 |
|
||
|
|
|
|
|
|
||
|
dq2 |
= f2(q1, q2). |
(1.108) |
||||
|
dt |
||||||
|
|
|
|
|
|
||
В частном случае уравнения (1.108) могут совпадать с системой уравнений Гамильтона, например описывающих динамику одномерного нелинейного осциллятора. Тогда переменная q1 будет иметь смысл обобщенной координаты, а q2 – обобщенного импульса.
Особые точки (точки стационарных состояний) системы(1.108) определяются из уравнений
f1(q1, q2) = 0, f2(q1, q2) = 0,
а поведение фазовой траектории можно определить, решая уравнение
dq2 |
= |
f2 |
(q1 |
, q2) |
. |
(1.109) |
|
dq |
f |
|
(q |
|
|||
|
1 |
, q ) |
|
||||
1 |
|
|
1 |
2 |
|
|
|
Уравнение (1.109) позволяет в каждой точке фазового пространства найти наклон касательной к траектории в данной точке и построить фазовый портрет по точкам. Направление, в котором движется фазовая точка, может быть найдено из системы уравнений (1.108).
Детальное исследование устойчивости производится так же, как и в одномерном случае, с помощью линеаризации уравнений движения (1.108) относительно малых отклонений динамиче-
ских переменных от их стационарных значений. Введем новые
динамические переменные x1(t) = q1(t) −q1s и x2(t) = q2(t) −q2s . Линеаризуя уравнения (1.108) относительно x1 и x2 , получаем
dx1(t) = a11 x1(t) + a12 x2(t), dt
dx2(t) = a21 x1(t) + a22 x2(t). (1.110) dt

§ 16. Системы с двумя степенями свободы |
67 |
Элементы матрицы
dfi(q1, q2)
aij =
dqj q=qs
вычисляются для стационарной точки и поэтому являются постоянными величинами.
Для решения системы воспользуемся подстановкой Эйлера
x |
(t) = A ep t, x (t) = B ep t. |
1 |
2 |
В результате получим систему линейных однородных уравнений для определения констант A и B, условием непротиворечивости которой является равенство нулю определителя
|
a11 − p |
− |
|
= 0. |
|
|
|
|
|
|
a21 |
a22 |
|
|
|
p |
|
Раскрывая определитель, получаем характеристическое уравнение второй степени относительно величины p
p2 − (a11 + a22) p + a11 a22 − a12 a21 = 0. |
(1.111) |
|||||||||||
В общем случае уравнение (1.111) имеет два комплексно со- |
||||||||||||
пряженных корня: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
T |
1 |
|
|
|
|
|
|
|
|
|
p1 2 = |
T 2 − 4 , |
|
||||||
|
|
|
|
|
± |
|
|
|||||
|
|
|
|
2 |
2 |
|
||||||
T = a11 + a22, |
|
= a11 a22 − a12 a21. |
(1.112) |
|||||||||
√ |
|
|
|
|
|
|
|
|
|
|
|
|
T |
2 |
− 4 |
= 0 |
и корни p1 и p2 характеристическо- |
||||||||
Пусть |
|
|||||||||||
го уравнения (1.111) различны. Тогда общее решение системы уравнений (1.110) является суперпозицией возможных частных решений и можно записать
x |
(t) = A ep1 t |
+ A ep2 t, |
|
1 |
1 |
2 |
|
x2(t) = A1 K1 ep1 t + A2 K2 ep2 t. |
(1.113) |
||
Константы A1 и A2 определяются из начальных условий, а константы K1 и K2 являются корнями уравнения
a12K2 + (a11 − a22)K − a21 = 0.

68 Глава 1. Термодинамика необратимых процессов
Последнее уравнение легко получить, если принять, что B = = A K .
Тип стационарной точки зависит от того, какими получились корни (1.112) характеристического уравнения (1.111). Существует всего шесть возможностей, которым соответствуют шесть типов стационарных точек. Схематически фазовые портреты двумерных систем изображены на рис. 9.
a ) T 2 − 4Δ > 0 , > 0, T < 0 . В этом случае p1 и p2 – действительные отрицательные числа. Система совершает апе-
риодическое затухающее движение, приближаясь к положению равновесия. Такая стационарная точка называется а с и м п - т о т и ч е с к и у с т о й ч и в ы м у з л о м.
b ) T 2 − 4Δ > 0 , > 0, T > 0 . В этом случае p1 и p2 – действительные положительные числа. Стационарная точ-
ка неустойчива. При любой флуктуации, приводящей к смещению фазовой точки из стационарного состояния, возмущение будет нарастать и система покинет окрестность стационарной точки (апериодическое самовозбуждение). Такая стационарная
точка |
называется а с и м п т о т и ч е с к и н е у с т о й - |
ч и в ы м у з л о м. |
|
c ) |
T 2 − 4Δ < 0 , T < 0 . В этом случае p1 и p2 – ком- |
плексные числа с отрицательной действительной частью. Система будет совершать затухающие колебания, асимптотически приближаясь к стационарной точке. Фазовый портрет такой системы напоминает закручивающуюся спираль. Стационарная точка является у с т о й ч и в ы м ф о к у с о м.
d ) T 2−4Δ < 0 , T > 0 . В этом случае p1 и p2 – комплексные числа с положительной действительной частью. Система
будет демонстрировать нарастающие по амплитуде колебания (самовозбуждение). Фазовый портрет такой системы напоминает раскручивающуюся спираль. Стационарная точка является
н е у с т о й ч и в ы м ф о к у с о м.
e ) > 0 , T = 0 . В этом случае p1 и p2 – чисто мнимые величины. Система будет совершать незатухающие колебания
в окрестности стационарной точки. Фазовый портрет представляет собой замкнутую кривую. Такого типа стационарные точки принято называть ц е н т р о м. Особая точка типа центр

§ 16. Системы с двумя степенями свободы |
69 |
устойчива по Ляпунову, но не является асимптотически устойчивой.
a |
b |
ñ |
|
|
s |
s |
s |
|
|
|
|
d |
e |
f |
s |
s |
|
|
s |
|
|
|
Рис. 9. Основные типы стационарных точек для динамической системы с двумя степенями свободы:
a – асимптотически устойчивый узел; b – асимптотически неустойчивый узел; c – асимптотически устойчивый фокус; d – асимптотически неустойчивый фокус; e – стационарная точка типа центр; f – седловая стационарная точка
f ) T 2 − 4Δ > 0 , < 0 . В этом случае p1 и p2 – действительные числа, имеющие разные знаки. Траектории фа-
зовой точки представляют собой гиперболические кривые, разделенные сепаратрисами (прямые линии на рис. 9f ). Стационарная точка называется с е д л о в о й. Поскольку при t → ∞ фазовые траектории уходят на бесконечность, седловая точка является неустойчивой стационарной точкой. Такие системы характеризуются наличием двух состояний (системы триггерного типа).
Приведенная выше классификация основывалась на предположении, что имеется два различных решения характеристического уравнения (1.111). Такие точки называются стационарными точками о б щ е г о п о л о ж е н и я. Возможны ситуации, при которых = 0 . Такие особые точки имеют название м н о ж е с т в е н н ы х. Анализ поведения фазовых траекторий в окрестности множественных особых точек может оказаться достаточно сложным, но, к счастью, этот случай можно не

70 Глава 1. Термодинамика необратимых процессов
анализировать, поскольку при небольшом «шевелении» (изменении параметров системы) множественные особые точки распадаются на две или более особые точки общего положения.
Задача 1.4
Для рассмотренной выше модели «хищник – жертва» Вольтерра – Лотки
n˙ 1 = γ1 n1 − β n1 n2, |
|
n˙ 2 = β n1 n2 − γ2 n2 |
(1.114) |
с численными значениями параметров γ1 = 0, 3712, β = 0, 0097 , γ2 = 0, 3952 определить стационарные значения популяций ns1 , ns2 , найти решение характеристического уравнения для линеаризованной модели и определить возможные типы стационарных точек в этой модели. Найти решение линеаризованной системы уравнений движения для небольших начальных отклонений чисел популяции от стационарных значений. Определить характер движения фазовой точки в окрестности стационарных точек. Выяснить, зависят ли типы стационарных точек в этой модели от численных значений параметров.
Решение
Стационарные значения популяций находим из уравнений
γ1 n1 − β n1 n2 = 0, β n1 n2 − γ2 n2 = 0.
Эта система имеет два решения. Первое решение является очевидным: ns1 = 0 , ns2 = 0 . Вторая стационарная точка соответствует
значениям ns = γ2/β = 40, 7423 ; ns = γ1/β = 38, 2680 . Рассмотрим |
||
1 |
2 |
|
вначале поведение системы вблизи второй стационарной точки. |
||
Введем новые sдинамические |
переменные |
x1(t) = n1(t) − n1s |
и x2(t) = n2(t) − n2 . Линеаризуя |
уравнения (1.114) относительно |
|
x1 и x2 , получаем |
|
|
x˙ 1 = (γ1 − β n2s ) x1 − β n1s x2, |
|
|
x˙ 2 = β n2s x1 − (γ2 − β n1s ) x2. |
(1.115) |
|
Сравнивая (1.115) и (1.110), легко убедиться, что в рассматрива- |
||
емом случае a11 = a22 = 0 , a12 = −β n1s = −γ2 , |
a21 = β n2s = γ1 , |
|
T = 0 , = a11 a22 − a12 a21 = γ1 γ2 > 0 . |
|
|
