Добавил:

Adamant Студент, если у тебя есть завалявшиеся работы, то не стесняйся, загрузи их на СтудентФайлс! Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Петербургский государственный университет путей сообщения им. императора Александра I

Предмет:

Теоретические основы электротехники

Файл:

Бутырин Алексейчик Сборник задач по ТОЭ т1

.pdf

Скачиваний:

822

Добавлен:

09.12.2021

Размер:

4.92 Mб

Скачать

☆

<<< < Предыдущая 32 33 34 35 36 37 38 39 40 41 42 4344 / 6044 45 46 47 48 49 50 51 52 53 54 55 56 > Следующая >>>

следовательно,

duC

U – uC

---------

-----------------

Фазовая траектория — линейная функция.

Начальные условия:

(0) =

duC

U – uC

(0)

U – UC0

---------

---

i(0) = -------------------------

---------------------

Фазовая траектория проходит через точки (0; U) и

;U---------------------– UC0

так как в установившемся режиме при t = ×

= U;

duC

= 0 ,

C уст

---------

dt уст

а при t = 0 (рис. 3 к задаче 8.19(р))

(0) = U

;

duC

U – UC0

---------

---------------------

duC

3dt 3U

2RC Движение изображающей точки

1вниз

	U
RC			Процесс
			Процесс
U		2	апериодический,
2RC		2	особая точка — узел
2RC			особая точка — узел
			(состояние равновесия)

– U

u(t)	i
L
C	u
Рис. 4 к задаче 8.19(р)

Рис. 3 к задаче 8.19(р)
2. Рассчитать	аналитически и построить	графически на фазовой
di
плоскости i; ----	траекторию процесса (рис. 4	к задаче 8.19(р)), вызван-
dt

ного переключением рубильника в схеме без разрыва цепи для случаев: 1) i = U = 0; 2) U ≠ 0, i = 0; 3) U ≠ 0, i ≠ 0, U = u(0), i = i(0).

Решение. Записываем дифференциальное уравнение цепи по второму закону Кирхгофа

di	1
L----	+ ---	∫i dt = 0	,
dt	C

431

решаем его относительно i;

---- :

d2i

L-------

--- = 0

-------

–------- .

d2i

Пусть i = x; ---- =

y ;

------- =

----- .

Тогда

dy dx

-----

= –-------

;

----- ----- = –-------

dx dt

-----y

= –-------

y dy =

–-------x dx ,

интегрируем и получаем

---- + K

–-------

----

LC 2

Так как ω

= -------

— собственная частота колебательного контура,

окончательно имеем:

y2 + ω2x2 = K2

(1)

или

----

—уравнение эллипса.

Постоянная интегрирования K определяется из начальных усло-

x2	y2
вий. Уравнение (1) можно представить в виде -----------------	+ ------ = 1 . Это
K2 ⁄ ω2	K2
0
	K
уравнение соответствует уравнению эллипса с полуосями ------ и		K

(рис. 5 к задаче 8.19(р)): 1) i = U = 0.

Из уравнения Кирхгофа

0 = L			di		+ u		(0)	di	= 0 ,
0 = L			----		+ u		(0)	----	= 0 ,
			dt			C		dt
			dt					dt
	di				0				0
	di
т.е. x = i = 0; y =	----	= 0		, по уравнению эллипса определяем K = 0.
	dt

Эллипс вырождается в точку (начало координат);

432

y		di	Движение
		y = dt на фазовой плоскости
		m	по часовой стрелке
		m
2K		U0
2K	x	L
		L

		Фокус		x = i
2K		n	U0
0				L
			0
Рис. 5 к задаче 8.19(р)		Рис. 6 к задаче 8.19(р)

2) U ≠ 0; i = 0.

Из уравнения Кирхгофа

0 = L

+ U

----

–------ ,

⁄

т.е. x = i = 0; y =

---- =

–------

, тогда

------

= 1

; --------------

= 1

K = ±------ .

Следовательно, полуоси эллипса равны ----------

------ .

ω L

Переходный процесс обозначен на фазовой плоскости в виде замкнутой траектории, так называемый фазовый цикл. Периодические процессы характеризуются тем, что фазовая траектория пересекает ось абсцисс под прямым углом (рис. 6 к задаче 8.19(р)).

При колебательном процессе особая точка в общем случае называется фокус, если затухание отсутствует, — центр.

Если U > 0, то начальная точка будет самой нижней точкой

эллипса m, если U < 0, то начальная точка n. Постоянная интегриро-

вания определяется из начальных условий, т.е. из уравнения эллипса при подстановке в него t = 0;

3) U ≠ 0; i ≠ 0.

Из уравнения Кирхгофа

	di			di	U
					U
0 = L		+ U			0
0 = L	----	+ U		----	= –------ .
	dt		0	dt	L
		0			0
		0			0

Подставляем в уравнение эллипса t = 0, решение имеет вид:

			2					2					2
		i			U							U
		i	0		U			0	= 1 ω2i2 +			U	0 = K2 ,
-----------------			0	+	------------			0	= 1 ω2i2 +			------	0 = K2 ,
	2			2		2			2	0	0		2
	2			2		2			2				2
K			⁄ ω	0	L		K					L

433

где

K = ±

------ = ±

2 2 0

ω i + ------ — малая полуось эллипса;

0 0 L2

i + ------------ — большая полуось эллипса.

ω2L

Большая полуось эллипса откладывается по оси токов, ее значе-

			2		0
ние соответствует максимальному току, т.е. I	=	i		+ ------------
	max		0		2
				2	2
				ω	L
				0

(рис. 7 к задаче 8.19(р)).

	U		2
02i02	+	0
		2
		L

di			Движение
y = dt			на фазовой плоскости
			по часовой стрелке
				x = i
			m
		= i 2	U	2
I	max	= i 2	+	0
	max	0	2L2
			0
Рис. 7 к задаче 8.19(р)

Полученные фазовые траектории в виде эллипсов соответствуют незатухающим синусоидальным колебаниям. Амплитуда колебаний равна полуоси эллипса, направленной по оси абсцисс, а частота равна отношению вертикальной полуоси к горизонтальной (с учетом масштабов).

В реальном колебательном контуре всегда есть некоторые потери, которыми нельзя пренебречь. За период колебаний амплитуда тока уменьшается и фазовые траектории приобретают вид спиралей, завивающихся вокруг начала координат.

8.20(р). Дано: Е = 9 В, R = 9 кОм, С = 0,1 мкФ (рис. 1, а к задаче 8.20(р)); вольт-амперная характеристика нелинейного элемента i(u) аппроксимирована тремя отрезками прямых (рис. 1, б к задаче 8.20(р)): fb, bd, dc.

434

			i, мА				c
			6				c	i(u)
			6					i(u)
t = 0			5
t = 0			4
E	iC	i(u)	4		d
	iC	i(u)	E 3		d
uC	C	u	E 3					E – u
uC	C	u	R 2			p		E – u
R			1					R
i1			1	f	a		b			E
			0		1	3	5	7	9	u, В
	а)							б)
		Рис. 1 к задаче 8.20(р)

Требуется:

построить фазовые траектории для напряжения на конденсаторе; установить устойчивость состояния равновесия; найти период колебаний; по фазовой траектории определить зависимость uС(t).

Решение. Применим метод фазовой плоскости, учитывая особенности фазовых траекторий, определяемых отрезками прямых.

1. Для построения фазовых траекторий у(х), где х = u ; у = duC/dt,

составим дифференциальные уравнения схемы по законам Кирхгофа:

iC =	E – uC
iC =	---------------- – i(u) , uC = u,
		R
duC		1	E – uC
duC		1	E – uC	– i(uC )
---------	=	---	-----------------	– i(uC )	.
dt		C	R

Дифференциальное уравнение для напряжения на конденсаторе, В/с,

duC

E – uC

– i(uC )

9 – uC

– i(uC)

---------dt

C---

-----------------

= 10

----------------

æ10

где учтено, что ток задан в миллиамперах. Фазовая траектория построена на рис. 2, а к задаче 8.20(р).

Свойства фазовой плоскости позволяют указать стрелками возможные направления движения изображающей точки. Моменту времени t = 0 соответствует точка f, так как i(0) = 0. Состояние равнове-

duC

сия --------- = 0 определяется точкой р. Первоначально с увеличением dt

напряжения uC изображающая точка перемещается от точки f к точке b.

Из точки b движение изображающей точки к точке р невозможно (в соответствии с указанным направлением движения). Но изображающая точка не может остаться и в точке b, поскольку точка b не определяет состояния равновесия. Поэтому изображающая точка из точки b скачкообразно (при неизменном напряжении uC) переходит в точку с

435

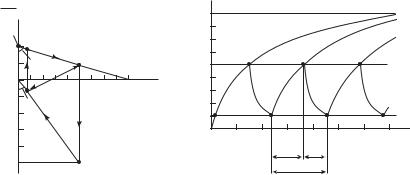
(показано штриховой линией). Далее аналогично из точки d происходит скачок к точке а, откуда изображающая точка снова движется к точке b и т.д., получается непрерывное движение по замкнутой фазовой траектории аbсdа — предельному циклу, т.е. происходят периодические незатухающие колебания. На рис. 2, б к задаче 8.20(р) сплошными линиями показана зависимость uC(t). Наклонные учас-

тки фазовой траектории аb и сd соответствуют отрезкам экспонент.
duC ,104 В/c										uC, В
dt										9
t = 0										8
t = 0	f	a								7
2		a								6
2
		1		b								b		b			b
1			p	b						5		b		b			b
1						E				5		c		c			c
0						E				4		c		c			c
0		1	3	5	7	9	u		, В	4
		1								3
–1	2d							C		3
–1	2d							C		2	a	d	a		d	a
–2										1	a		a			a
–3										1	f
–3										0	0,2	0,4	0,6	0,8		1,0	1,2	1,4 t, c
–4										0	0,2	0,4	0,6	0,8		1,0	1,2	1,4 t, c
–4													tз	tр
–5				c										T
														T
				а)										б)
								Рис. 2 к задаче 8.20(р)

2.Устойчивость равновесия, определяемого точкой р, можно установить, рассматривая малые отклонения относительно этой точки. Как следует из указанных на рис. 2, а к задаче 8.20(р) возможных направлений движения изображающей точки, равновесие в точке р неустойчивое.

3.На графике uC(t) (рис. 2, б к задаче 8.20(р)) показан период

колебаний Т = t	+ t , где t	— время зарядки; t	— время разрядки
з	р	з	р

конденсатора. Зарядке соответствует участок аb фазовой траектории, разрядке — сd. Интервалы времени, необходимые для движения изображающей точки на этих участках, найдем по формулам:

t = x------------------------k + 1		– xk	ln y------------k + 1 =	--------------------------5 – 1	ln 1----------------æ104	= 2,775æ10–4 с;
з	yk + 1	– yk	yk	(1 – 2)104	2æ104
	yk + 1	– yk	yk	(1 – 2)104	2æ104
	t	=	--------------------------------1 – 5	ln 1----------------æ104	= 1,609æ10–4 c.
		р	(– 1 + 5)104 5æ104
			(– 1 + 5)104 5æ104

Период Т = t + t = 4,384æ10–4 с.

зр

436

4. Для определения периодически изменяющегося напряжения uС(t) учтем соответствие прямолинейного участка фазовой траекто-

рии и экспоненциальной зависимости. Так, для участка аb имеем:

	–t ⁄ τ	–t ⁄ τ		–t ⁄ τ
uCab = uуст + A1e	1 = E + A1e	1 = 9 – 8e		1 , так как в точке а
(рис. 2, а к задаче 8.20(р)) при t = 0 напряжение uCab(0) = 1 и А1 = 1 –
					–t ⁄ τ	–t ⁄ τ
– 9 = –8. Аналогично для участка сd: u			= u + A e		2 = –5e	2 ,
		Ccd	уст	2
так как здесь u	= 0.
уст

Постоянная времени τ экспоненциальной зависимости (рис. 2, а к задаче 8.20(р)) равна тангенсу наклона прямой на фазовой плоскости

к оси ординат (с учетом масштабов), т.е.
		uC		5 – 1		= 4æ10	–4
τ = tgα =		----------------------------	= --------------------------			= 4æ10		c;
1	1	(duC ⁄	dt) (2 – 1)104
		(duC ⁄	dt) (2 – 1)104
	τ = tgα = --------------------------		5 – 1		= 1æ10–4 c.
	2	2
		(5 – 1)104

Получилось τ > τ , т.е. процесс зарядки происходит медленнее,

чем процесс разрядки.

8.21.По кривым мгновенных значений напряжения, приведенным на рис. к задаче 8.21, а, б, в, построить качественно фазовые траектории на плоскости [du/dt; u]. Указать стрелками направление движения изображающей точки.

8.22.По фазовым траекториям, приведенным на рис. к задаче 8.22, построить качественно кривые мгновенных значений uС(t), Ψ(t).

8.23.Характеристика диода при прямом включении (рис. к задаче 8.23)

аппроксимирована зависимостью i = au2.

Полагая, что параметры элементов схемы Е = const, R и С известны, получить уравнение фазовой траектории тока [di/dt = f(i)].

8.24.Для потокосцепления катушки в задаче 8.1(р) при аналитической аппроксимации найти уравнение фазовой траектории [dΨ/dt = f(Ψ)].

8.25.Вольт-амперная характеристика газоразрядного элемента (рис. а к задаче 8.25) приведена на рис. б к задаче 8.25. Параметры линейных элементов: J = 5 мА, С = 0,1 мкФ.

Построить фазовый портрет в координатах [duC/dt; uC].

Определить устойчивость состояния и найти период Т возможных колебаний.

8.26.Заданы параметры элементов в схеме (рис. а к задаче 8.26):

Е= 200 В, R = 2 Ом, С = 100 мкФ, характеристика индуктивной катушки Ψ(i) приведена на рис. б к задаче 8.26.

437

u
Um
0	T	t
T/2	T	t
–Um
а)

				u
				Um
						t2
					t1				t3	t
				–Um
					б)
				u
				0	t1	t2			t
					t1	t2			t
					в)
					Рис. к задаче 8.21
du	C		4			d
	C	=y, 10	4	В/c		dt =y,
dt		=y, 10		В/c		dt =y,
		t = 0		a	b	102 Вб/c
	5	t = 0		a	b
	5			10	30
	0			10	30	2
	0	5		15 20 25	35 uC=x, В	2
–5		5		15 20 25	35 uC=x, В	1				t = 0
–10				d	–20	–10	0		10	20	= x,
–10					–20	–10	0		10	20	= x,
–15						–1					10–2 Вб
–15						–2	t		t1		10–2 Вб
–20							t	2	t1
								2
–25					c

а)

б)

Рис. к задаче 8.22

438

i		i, мА
u	i	30					i(u)
u
J		20
E	C	20
E

C		10
		10
R		0		10	20	30	u, В
R					б)
а)					б)
Рис. к задаче 8.23	Рис. к задаче 8.25
	, 10–2 Вб
	10
	9
i	5
E	5
E
C	0
–30	–20 –10	10	20	30	i, А
R		–5
		–5
		–9
		–10
а)		б)
Рис. к задаче 8.26
Требуется:
а) найти уравнения фазовой траектории и построить фазовый пор-
трет на плоскости х = Ψ, у = dΨ/dt;
б) определить период колебаний T;
в) найти период при уменьшении ЭДС Е до 20 В.
8.27. Полагая в схеме (рис. к задаче
8.27) начальные условия нулевыми,							iL
J = const и диод идеальным, составить							iL
J = const и диод идеальным, составить
	J
уравнение фазовой траектории тока iL							L
							L
[у = f(х), где х = iL, у = diL/dt].					C

8.28. Конденсатор емкостью С = = 1000 пФ замыкается на неразветв-

ленную цепь, состоящую из резистора

Рис. к задаче 8.27

сопротивлением R = 100 кОм и диода

с вольт-амперной характеристикой i = 10–6u2 + 4,2æ10–6u3 (ток i в

амперах, напряжение u в вольтах). Напряжение на конденсаторе в

момент замыкания uС(0) = 2 В.

Найти уравнение фазовой траектории напряжения на диоде

д
--------	= f(u	) .
dt		д

439

8.4. МЕТОД УСРЕДНЕНИЯ

8.29(р). В цепи (рис. 1 к задаче 8.29(р))

периодический процесс имеет колеба-

тельный характер. Начальное напряже-

ние на конденсаторе

uC(0)

= U0. При

известных значениях R, С и заданной

–

вольт-амперной характеристике в виде

i(Ψ) = (1/L )(Ψ + kΨ3) методом усредне-

ния определить зависимости амплитуды

Рис. 1 к задаче 8.29(p)

потокосцепления, фазы и частоты соб-

ственных колебаний от времени.

Решение. Запишем уравнения по законам Кирхгофа для схемы

рис. 1 к задаче 8.29(р):

iС = iR + i(Ψ); uL – uC = 0; uL – uR = 0.

Учитывая, что

duC

duL

d2Ψ

1 dΨ

= –C---------

= –C

--------

= –C----------

и iR = ----- =

----- =

--- ------- ,

R dt

уравнения сведем к однородному нелинейному дифференциальному уравнению второго порядка для потокосцепления:

d2Ψ			1 dΨ	1		k		3
----------		+ ------- -------		+ ----------Ψ + ----------			Ψ		= 0 .
	2	RC dt		L C	L C
dt				0		0
Введя обозначения 2δ = 1/(RС), ω2					= 1/(L С), К = k/(L С), получим:
				0		0			0
	d2Ψ		2		dΨ			3
	----------		+ ω Ψ = – 2		δ-------	– KΨ			.
		2	0		dt

Предположим, что затухание 2δ и коэффициент аппроксимации k

малы; решение будем искать в виде
dΨ
θ = ωt – ϕ, Ψ = a cosθ, -------	= –aω sin θ , θ	= ω t – ϕ.
dt	0	0

Уравнения установления амплитуды а = а(t) и фазы ϕ = ϕ(t):

da			1	2π		0 sin θ – Ka	3		3
-----	= –		-------------	∫	(2δaω	0 sin θ – Ka		cos	θ) sin θ dθ ;
dt			2πω
			0	0
				0
				2π
dϕ			1			0 sin θ – Ka	3		3
------	=	-----------------		∫	(2δaω	0 sin θ – Ka		cos	θ) cos θ dθ .
dt		2πω a
			0	0
				0

440

<<< < Предыдущая 32 33 34 35 36 37 38 39 40 41 42 4344 / 6044 45 46 47 48 49 50 51 52 53 54 55 56 > Следующая >>>

Соседние файлы в предмете Теоретические основы электротехники

#
11.07.20208.85 Mб233Ekzamen_Toe.docx
#
11.07.20201.08 Mб42Obschiy_test_s_numeratsiey0.pdf
#
12.09.202025.09 Кб16TL_2017.doc
#
09.12.20214.92 Mб822Бутырин Алексейчик Сборник задач по ТОЭ т1.pdf
#
10.06.20215.65 Mб100Ответы на экзамен лето 2 курс.docx
#
16.03.20211.61 Mб28ТОЭэкзам3sem.doc