Добавил:

Lyubochka Студент архфака КНУБА (КИСИ) 2019-2023 (ﾉ◕ヮ◕)ﾉ*:･ﾟ✧ Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет строительства и архитектуры

Предмет:

Сопротивление материалов

Файл:

БУДIВЕЛЬНА МЕХАНIКА. Посiбник-2018.pdf

Скачиваний:

112

Добавлен:

28.11.2021

Размер:

17.29 Mб

Скачать

☆

<<< < Предыдущая 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 4546 / 5346 47 48 49 50 51 52 53 > Следующая >>>

ДО ЗМІСТУ ПОСІБНИКА

16. Динамічний розрахунок рам

16.1.Короткі відомості про розрахунок на динамічні дії

16.2.Приклад динамічного розрахунку рами

16.2.1.Розрахунок на вільні коливання

16.2.2. Розрахунок на змушені коливання безпосереднім розв’язанням диференціального рівняння руху

16.2.3. Розрахунок на змушені коливання розкладанням навантаження по головним формам коливань

16.3. Виконання розрахунково-графічної роботи з використанням комп’ютерної програми

16.4. Задачі для самостійного опрацювання

16. Динамічний розрахунок рам

16.1.Короткі відомості про розрахунок на динамічні дії

Однією з найголовніших характеристик коливальних систем є число динамічних ступенів вільності тобто кількість незалежних геометричних параметрів узагальнених координат які визначають положення всіх мас системи при її деформаціях

При визначенні числа ступенів вільності динамічної системи зручно кожну зосереджену масу умовно закріплювати кінематичними в’язями так щоб маса при обраних передумовах розрахунку зробилась нерухомою Мінімальне число кінематичних в’язей які необхідно ввести для повного закріплення всіх мас характеризує число динамічних ступенів вільності коливальної системи

Вільними називають коливання системи яка в початковий момент часу виводиться зі стану рівноваги після чого причини збудження усуваються і система продовжує рух за відсутності зовнішніх дій Коливання відбуваються за рахунок запасу енергії яку одержала система при початковому збудженні

Змушені коливання характеризуються тим що система перебуває під постійною дією зовнішніх динамічних навантажень Енергія яка необхідна для підтримки процесу коливань здобувається за рахунок зовнішніх дій

Вільні коливання системи з n ступенями динамічної вільності характеризуються системою лінійних однорідних диференціальних рівнянь

		y1 m1 y1 11	m2 y2 12	mn yn 1n;
		y2 m1 y1 211	m2 y2 22	mn yn	2n;	(16.1)
						(16.1)
		yn m1 y1 n1	m2 y2 n2	mn yn nn.
	Тут y1, y2 ,	, yn можливі переміщення зведених мас m1, m2 ,			,mn	системи зведеною масою
~	назвемо сумарну масу яка зміщується в напрямі переміщення yi ),					ik переміщення зведеної
mi						ik переміщення зведеної
маси в напрямі		від дії одиничної сили в напрямі k.
	Система диференціальних рівнянь 16. може бути записана в матричній формі
		Dm y y 0 .				(16.2)
Тут m матриця мас

			2
	m1
m	m2	;	(16.3)
m		;	(16.3)

D матриця податливості коливальної системи

11	12	1n
D 21	22	2n ;	(16.4)
n1	n2	nn

y, y вектори можливих переміщень та їхніх других похідних за часом

y	y	y	2	y	T ,
	1		2		n
y	y	y	2	y	T .
	1		2		n

Розв’язок системи диференціальних рівнянь 16. розшукується у вигляді

y1 a1 sin	t	,	y1 a1	2 sin	t	;
y2 a2 sin	t	,	y2 a2	2 sin	t	;
yn an sin	t	,	yn an	2 sin	t	.

(16.5)

(16.6)

(16.7)

Тут a1,a2, ,an амплітуди можливих переміщень				мас системи	циклічна колова
частота вільних коливань що характеризує кількість повних циклів коливань за 2 секунд;
початкова фаза коливань
Підстановка розв’язків 16.	в систему диференціальних рівнянь 16.				перетворює	її на
систему лінійних алгебраїчних рівнянь
m1 11 a1		m2 12a2		mn 1nan 0,
m1 21a1	m2	22 a2		mn 2nan 0,	(16.8)
					(16.8)
m1 n1a1		m2 n2a2	mn	nn an 0.
Тут позначено
		1 .			(16.9)
		2

Система однорідних алгебраїчних рівнянь 16. складена відносно амплітуд переміщень зведених мас Система матиме ненульовий розв’язок якщо її визначник дорівнює нулю

						3
m1	11	m2	12	mn 1n
D m1	21	m2	22	mn	2n 0.	(16.10)
m1	n1	m2	n2	mn	nn

Рівняння 16. називається "віковим" або частотним Воно є характеристичним рівнянням системи 16. Невідомим у "віковому" рівнянні є величина яка в системах з n ступенями вільності має n дійсних значень.

"Вікове" рівняння може бути представлене в матричній формі

E V 0 ,

(16.11)

де E одинична матриця

A m1

(16.12)

m1 n1

m2 n2

mn nn

Оскільки

"вікове"

рівняння 16.

має n дійсних

коренів

можна

дійти висновку що

система що має n ступенів динамічної вільності

може коливатися з n частотами

астоти власних

коливань виражаються виходячи зі співвідношення

16.

за формулою

1 .

(16.13)

Сукупність усіх частот

i i 1,2,

, n

утворює спектр частот Розташуємо частоти в порядку

їх збільшення

n Найменша частота

1 називається частотою основного тону

коливань а решта частот обертонами.

Кожній

частоті

тобто

кожному

кореню

i=1,2,

відповідає

сукупність

амплітуд

a1,a2 , ,an

які визначаються з точністю до множника

Набір амплітуд

що відповідає якійсь

певній частоті

характеризує форму

деформації

системи

яка

відповідає

означеній

частоті і

називається формою власних коливань

исло

називається власним або характеристичним числом матриці

астоти

кожна з

яких відповідає якомусь із власних чисел називають власними частотами Очевидно що першій частоті вільних коливань яка є найменшою у спектрі відповідає найбільше власне число тобто

1 2 3 n ,

			4
причому найбільше власне число	1 вважається старшим		Множина амплітуд які відповідають
якому-небудь власному числу утворюють вектор V який називається власним вектором.
Таким чином квадратна матриця A (16.		порядку n має n власних чисел і n власних векторів
Для визначення частот вільних	коливань	власних частот	необхідно обчислити власні числа

матриці A а для визначення амплітуд власні вектори Власні числа мають певні властивості

Сума власних чисел дорівнює сумі головних коефіцієнтів сліду матриці A:

i 1

i Sp A m i ii . (16.14)

i 1

Добуток власних чисел дорівнює визначнику матриці A:

	n
	i 1	2	n Det A .		(16.15)
	i 1
Переміщення мас системи характеризує деформовану вісь споруди				так звану	форму
коливань	орми коливань які визначаються		амплітудами що входять	до складу	власних

векторів називають головними формами коливань Отже системи з n ступенями вільності мають

n головних форм коливань а переміщення будь-якої маси j в будь-який момент часу t			може
розглядатися як накладання n головних форм коливань
yj a j1 sin 1t	1 aj2 sin 2t 2	a jn sin nt n
n	it i .
a ji sin	it i .	(16.16)
i 1
Тут a ji амплітуда переміщення y j	в формі коливань .
На цій підставі можна вважати	що кожна маса системи з n ступенями вільності в процесі
вільних коливань коливається водночас з n власними частотами
оловні форми коливань мають такі властивості
1. У будь-який момент часу	співвідношення між	амплітудами не змінюється	тобто

деформована вісь споруди			що відповідає головній формі коливань	зберігає свою форму дефор-
мації	Тому	такі деформації називають стоячою хвилею. Так		для	сукупності амплітуд
a1i , a2i ,	, a ji ,	, aki , , ani	будь-якої головної форми власних коливань		яка відповідає власній
частоті	i можна записати

yji	aji	const .	(16.17)
yki	aki

2. Сума добутків мас системи на відповідні амплітуди двох головних форм коливань дорівнює нулю ей висновок називається властивістю ортогональності головних форм коливань Так

для двох головних форм				T			a1i , a2i ,		T
для двох головних форм	Vk		a1k ,a2k , ,a jk ,	,ank	і	Vi	a1i , a2i ,	,a ji , , ani	які
відповідають власним частотам		i і	k можна записати
			n
			mj ajk aji	0 .					(16.18)

j 1

Мета розрахунку на вільні коливання полягає у визначені частот і форм власних коливань Змушені коливання системи з n ступенями вільності відповідають системі диференціальних

рівнянь руху

		y1 m1 y1 11			m2 y2 12			mn yn 1n	1 pP(t);
		y2 m1 y1		211	m2 y2 22			mn yn 2n	2 p P(t);
									(16.19)
		yn m1 y1		n1 m2 y2 n2				mn yn nn	npP(t).
і самі рівняння в матричній формі набувають вигляду
					Dm y y DP ,				(16.20)
де P P	P	P T вектор зовнішніх динамічних навантажень розкладений по напрямах
1	2	n
можливих переміщень коливальної системи
Розв’язок системи 16.			розшукується у вигляді
					y1 A1 sin		t,
					y2 A2 sin			t,	(16.21)
									(16.21)
					yn An sin			t.
Підставивши розв’язок			16.2	до рівнянь		16.		одержуємо систему алгебраїчних рівнянь У
разі дії вібраційного навантаження P(t) P0 sin						t система набуває вигляду

1 p

P 0;

m 2

12 2

1n n

2 p

(16.22)

21 1

m 2

P 0.

n1 2

n2 2

Тут B1, B2 , , Bn амплітудні величини сил інерції які діють в напрямах можливих переміщень і виражаються співвідношеннями

B m A 2	,	B m A 2	,	, B m A 2.	(16.23)
1 1 1		2 2 2		n n n

Амплітудні величини динамічних зусиль M ,Q , N можуть бути визначені на базі принципу незалежності дії за формулами накладання

n
M M B M P0 ;
i 1
n
Q Q B Q P0 ;	(16.24)

i 1

N N B N P0 ,

i 1

де Mi ,Qi , Ni відповідно згинальні моменти поперечні і поздовжні сили від дії одиничних сил інерції M p ,Qp , Np зусилля від статичної дії одиничного зовнішнього навантаження

Амплітуди переміщень можуть бути визначені на базі формул 16.23)

A	B1		,	A	B2		,	,	A	Bn		(16.25)
1	m	2		2	m	2			n	m	2
	1				2					n

або за формулою Максвелла-Мора

Ai i	Mi M	dx.	(16.26)
	EI

Розрахунок динамічної системи на змушені коливання може виконуватись способом розкладання навантаження по головним формам коливань Такий підхід дозволяє виконати розрахунок на змушені коливання без складання і розв’язування системи рівнянь дея способу полягає в розкладанні зовнішнього навантаження що діє на маси системи на низку інших навантажень кількість яких дорівнює числу ступенів вільності Сили що діють на маси в кожному завантаженні мають бути пропорційні силам інерції однієї з головних форм коливань При такому

завантаженні коливання відбуватимуться по відповідній головній формі Отже замість одного дійсного навантаження з’являються кілька інших завантажень зовнішні сили в яких пропорційні силам інерції головних форм коливань При кожному з таких завантажень система що має n ступенів вільності коливатиметься з однією спільною для всіх мас частотою тобто буде поводитися як система з одним ступенем вільності і може розраховуватися відповідними способами Кінцеві результати для вихідної схеми можуть бути отримані додаванням результатів розрахунків на кожне навантаження окремо Таким чином розрахунок системи з n ступенями вільності може бути зведений до розрахунку n систем з одним ступенем вільності.

Для одержання сили в напрямі що відповідає певній головній формі j необхідно скористатися формулою

n
Pi (t) miaik Hk ,	(16.27)

k 1

де коефіцієнт H j визнається зі співвідношення

		n
		Pi (t)aij
H	j	i 1	.	(16.28)
	j	n
		miaij2

i 1

Унаведених формулах Pi t зовнішні сили що діють у напрямах можливих переміщень зведених мас системи m~i , aij відповідні амплітуди даної форми коливань

Від кожного утвореного навантаження будуються складові епюри Дійсні епюри можуть бути одержані як сума складових епюр помножених на відповідні динамічні коефіцієнти

1		1	,	2		1	,	3		1	, .	(16.29)
	1	1 2			1	2 2			1	3 2

16.2. риклад динамічного розрахунку рами


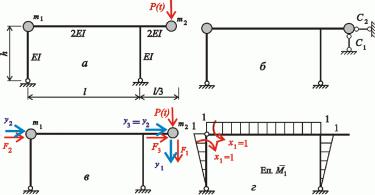
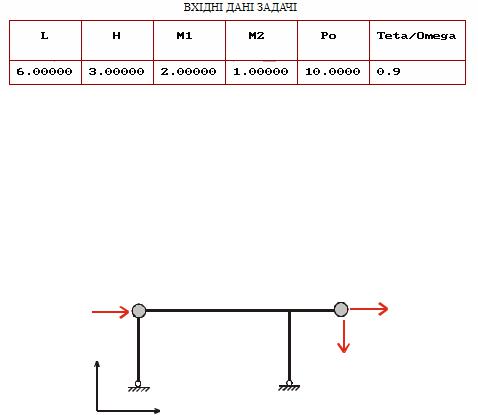
Розглянемо		невагому рами наведену				на	рис 16.1,а	еометричні розміри рами
характеризуються			параметрами	l 6 м,	h 3 м		На рамі розташовано дві точкові маси
m1 2m,	m2	m	Зовнішнє	навантаження			вібраційна	сила P t P0 sin t причому
P0 10 кН ,	0,9		1 Необхідно виконати динамічний розрахунок рами тобто розрахувати раму

на вільні і змушені коливання

Рис 16.1

16.2.1.Розрахунок на вільні коливання

изначення числа ступенів вільності

Для закріплення мас системи достатньо ввести два додаткових опорних стержня рис 16.1.б).

Вертикальне переміщення y1 маси m2 усувається постановкою стержня C1 а вертикальне переміщення маси m1 дорівнює нулю оскільки при згині рам поздовжніми деформаціями стержнів можна нехтувати оризонтальні переміщення обох мас усуваються постановкою одного додаткового опорного стержня C2 Отже переміщення y2 і y3 лінійно залежні До того ж очевидно що

y2 y3 .	(16.30)
Таким чином задана система має два динамічних ступеня вільності
n ин 2 .	(16.31)

Напрями можливих переміщень показано на рис 16.1,в У подальшому ці напрями вважатимемо за додатні Тут також показано додатні напрями сил інерції F1, F2 , F3 , які зумовлені рухом точкових мас системи

Складання диференціальних рівнянь руху

Запишемо можливі незалежні переміщення як суми переміщень від дії сил інерції

y1	11F1	12 F2	13F3 ,	(16.32)
y2	21F1	22 F2	23F3.	(16.32)
y2	21F1	22 F2	23F3.
Враховуючи рівність вертикальних переміщень 16.			можна записати
	13	12 ,		(16.33)
		22.		(16.33)
	23	22.

Сили інерції виразимо через можливі незалежні переміщення y1 і y2 :

F1 m1 y1 my1,
F2 m2 y2	my2 ,		(16.34)
F3 m1 y3 2my2.
Система рівнянь 16. з урахуванням 16.	і 16.	набуває вигляду
m 11 y1 y1	3m 12 y2 0,		(16.35)
m 21 y1 3m 22 y2 y2 0.			(16.35)
m 21 y1 3m 22 y2 y2 0.

У диференціальних рівняннях 16. зведені маси які переміщуються в напрямах незалежних переміщень y1 і y2 дорівнюють

m1 m2	m,		(16.36)
m2 m1 m2 3m.			(16.36)
m2 m1 m2 3m.
Отже матриця мас має вигляд
m m	0	.	(16.37)
0	3m
Розв’язання диференціальних рівнянь руху
Розв’язок системи диференціальних рівнянь	16	розшукуємо у вигляді
y1 a1 sin	t	,	(16.38)
y2 a2 sin t		.	(16.38)
y2 a2 sin t		.

Після підстановки розв’язків 16. до рівнянь 16. одержуємо систему однорідних алгебраїчних рівнянь

m 11 a1			3m 12	0,	(16.39)
m 21	3m		22 a2	0,	(16.39)
m 21	3m		22 a2	0,
де позначено
		1 .			(16.40)
		2

Розрахунок заданої рами на одиничні дії

Для обчислення коефіцієнтів системи рівнянь 16. необхідно побудувати епюри згинальних моментів що виникають у заданій схемі від дії одиничних сил інерції Отже виникає потрібність розрахунку рами на дію статичних навантажень

Задана схема статично	невизначувана	Дійсно n 3k	3 1 2 1	Для розрахунку
скористаємось методом сил	Основну систему одержимо за рахунок уведення шарніра у лівий
верхній вузол рами Одинична епюра M1 побудована на рис 16.1,г.
Система канонічних рівнянь методу сил складається з одного рівняння
	11 X1	1 p 0.		(16.41)

Одиничний коефіцієнт 11 не залежить від зовнішніх навантажень і може бути обчислений за формулою Мора

11	l M12			dx 2			1 1 3			2 1			1 1 6 1			5 .	(16.42)
	0	EI					EI	2		3		2EI				EI
	0
Розв’язавши 16.	маємо
						X1		1 p		EI				1 p .			(16.43)
								11			5
								11
Дійсна епюра згинальних моментів може бути побудована згідно формули
						M M1 X1 M .											(16.44)
Розрахунок на дію сили F1 1					рис.16.2,а).
Вантажна епюра M p1 показана на рис 16.2,б Вантажний коефіцієнт
		1 p				l	M1M p1		dx		1			1 6 1	3	.	(16.45)
		1 p				0	EI		dx		2EI			1 6 1	EI	.	(16.45)
							EI				2EI				EI

Розв’язок канонічного рівняння					16.		згідно до				16.43):
		X	1	EI			3	0,6 .									(16.46)
			1		5		EI
					5		EI

Рис 16.2

Дійсна епюра згинальних моментів від першого навантаження побудована за формулою (16. наведена на рис 16.2,в.

Розрахунок на дію сили F2 1 рис.16.2,г).
Вантажна епюра M p2 показана на рис 16.2,	Вантажний коефіцієнт

1 p	l	M1M p2			dx	1	1 6	1,5			1	3 3	2	1	7,5	.	(16.47)
1 p	0	EI			dx	2EI	1 6	1,5		EI		2	3	1	EI	.	(16.47)
		EI				2EI				EI		2	3		EI

Розв’язок канонічного рівняння			16.			згідно до			16.43):
			X	1	EI 7,5 1,5 .												(16.48)
				1		5 EI
						5 EI

Дійсна епюра згинальних моментів від другого навантаження побудована за формулою (16. наведена на рис 16.2,е.

Обчислення переміщень

Визначимо переміщення які входять до рівнянь 16. Для контролю кожне переміщення будемо обчислювати двома способами

11		l			M12			dx				6				0,62	4 0,42		1, 42 2 1			0,6 3	2 0,6
				0	EI						6 2EI										EI	2	3
				0
				1			2 2			2 2					3,533 ;
			2EI					2		3						EI
				l	M1M p1										6
11				0		EI				dx 6 2EI 0,6 0 4									0,4 1 1,4 2
				0
				1			2 2			2 2					3,533.
			2EI					2		3						EI
12		21			l				MEI1M2 dx 6 26EI 0,6 1,5 4 0 0,4 1, 4 1.5
								0
							1		0,6 3					2		1,5	1	0,6 3 2		1,5 1,5 ;
							EI				2			3			EI	2	3		EI
								l	M1M p2							6		0,6 0 4 1,5 0,4 3 1, 4
12		21						0		EI			dx 6 2EI					0,6 0 4 1,5 0,4 3 1, 4
								0
							1		0,6 3					2		3 1,5 ;
							EI				2			3		EI
		21				l		M p1M2								6						1,5
12		21				0			EI			dx 6 2EI 0 1,5							4 1 0 2 1,5			EI .
22		l			M22			dx 2				1				3 1,5	2 1,5		1	3 1,5 2 1,5 2			6,75	;
				0	EI							EI				2	3		2EI	2	3		EI
				0
				l	M2M p2											6
22				0			EI				dx	6 2EI 0 1,5 4							0 1,5 1,5 3
				0
			1		3 3				2		1,5				6,75.
			EI				2		3							EI
	Дані коефіцієнти складають матрицю податливості
																				3,533		1,5
																D		11	12		EI	EI
																		21	22		1,5	6,75
																					EI	EI
	Складання "вікового" рівняння
	Підставивши переміщення в систему 16.																				одержимо
																	3,533		a1			4,5a2	0,
																		1,5a1			20,25 a2		0.

(16.49)

(16.50)

Тут позначено

	EI		EI	.	(16.51)
	m		m 2

Отже для одержання динамічних характеристик системи необхідно обчислити власні значення власні числа і власні вектори матриці

A	3,533	4,5 .	(16.52)
	1,5	20,25

"Вікове" рівняння тобто умова наявності вільних коливань заданої рами матиме вигляд

Det A	E	3,533	4,5	0.	(16.53)
		1,5	20,25

изначення власних чисел матриці A

Розкривши визначник 16. одержуємо квадратне рівняння

Det A E 3,533

20,25

4,5 1,5 0;

2 23,783 64,793 0.

Корені квадратного рівняння є власними числами матриці A.


1,2 11,892	11,8922 64,793 11,892 8,573;
1	20,534,	(16.54)
2 3,139.		(16.54)
2 3,139.

еревірка власних чисел

Сума власних чисел має дорівнювати сумі головних коефіцієнтів сліду матриці A:

2	1
i	1	2	20,645 3,139 23,784;	(16.55)
i 1				(16.55)

Sp A 3,533 20,25 23,783.

Добуток власних чисел має дорівнювати визначнику матриці A:

2
i	1 2	20,645 3,139 64,804;
i 1			(16.56)
	3,533	4,5	(16.56)
Det A	3,533	4,5	64,793.
	1,5	20,25

Обчислення частот вільних коливань

Власні частоти вільних коливань визначаються на базі співвідношення 16.40):

	i		EI .
			m i
Отже маємо:

1		EI	0,22	EI ;
1		m 1		m
		m 1		m

2		EI	0,564		EI .
2		m 2			m
		m 2			m

изначення головних форм вільних коливань

(16.57)

(16.58)

Співвідношення амплітуд переміщень які визначають форму зігнутої осі рами при кожній власній частоті можуть бути знайдені з рівнянь 16.39).

Пер а головна орма

Підставимо величину	1 20,645 до рівнянь 16.						Маємо
	17,112a1		4,5a2			0;		(16.59)
	1,5a1 0,395					0.		(16.59)
	1,5a1 0,395					0.
Легко впевнитись що як з першого так і з другого рівняння отримаємо
		a1 0,263a2 .						(16.60)
Таким чином якщо амплітуда a2 1 то амплітуда					a1 0,263 Отже			можна записати для першої
форми
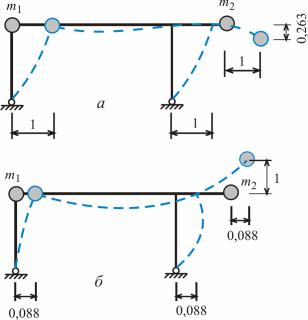
		a11		0,263			.	(16.61)
	V1	a21			1		.	(16.61)
		a21			1
Друга головна орма
Підставимо величину	2 3,139 до рівнянь		16.			Маємо
	0,394a1			4,5a2			0;	(16.62)
	1,5a1		17,111a2				0.	(16.62)
	1,5a1		17,111a2				0.
к з першого так і з другого рівняння отримаємо
	a2 0,088a1 .							(16.63)

					15
Таким чином якщо амплітуда a1 1	то амплітуда a2 0,088				Отже можна записати для другої
головної форми коливань
		a12	1	.	(16.64)
V2		a22	0,088	.	(16.64)
		a22	0,088

еревірка ортогональності головних форм вільних коливань

Перевіримо чи дорівнює нулю, згідно до 16.18), сума добутків мас і відповідних амплітуд двох головних форм вільних коливань

mj aj1aj2 m1a11a12 m2a21a22 m 0,263 1 3m 1 0,088

j 1

0,263m 0,264m 0,001m 0.

обудова головних форм вільних коливань

Перша і друга головні форми коливань побудовано на рис 16.3.а і 16.3.б відповідно

Рис 16.3

16.2.2. Розрахунок на змушені коливання безпосереднім розв’язанням диференціального рівняння руху

Система алгебраїчних рівнянь

Система лінійних алгебраїчних рівнянь для змушених коливань 16. для заданої схеми набуває вигляду

				1	B							B		1 p	P	0,
	11			m 2	1							12 2		1 p	0
				1												(16.65)
											1					(16.65)
					B			22			1	B	2 p		P	0
					21 1			22			2	2	2 p		0
										m2
або з урахуванням величин зведених мас
				1	B							B	1 p	P 0,
	11		m 2		1						12	2	1 p	0		(16.66)
										1						(16.66)
				21	B		22			1	2	B	2 p	P	0.
				21	1		22		3m		2	2	2 p	0
									3m
Тут B1, B2 невідомі амплітудні величини										сил		інерції		що		діють в напрямах можливих
переміщень і виражаються співвідношеннями
				B m A				2	mA 2 ,
					1	1	1				1					(16.67)
				B m A				2	3mA			2.				(16.67)
				B m A				2	3mA			2.
					2	2	2				2
Коефіці нти системи алгебраїчних рівнянь
До рівнянь 16.	входять переміщення							які були обчислені під час розрахунку на вільні
коливання і складають матрицю податливості									16.			Для визначення вантажних коефіцієнтів
1 p , 2 p необхідно	побудувати			в рамі		епюру			M p			зумовлену			дією одиничного зовнішнього
навантаження рис 16.4,а).
																2
						P0 = 1										1,4
						P0 = 1					0,6		0,4
													0,4

										0,6						0,6
													Еп Mp
		а											б
													б
							Рис 16.4
Означений вантажний стан збігається із								допоміжним					станом			від дії першої сили інерції
рис 16.2,а Тому епюра M p		рис 16.4,а				дорівнює епюрі M1							рис 16.2,в):
								M p		M1 .						(16.68)
Отже вантажні переміщення

1 p		l	M1M p	dx	l	M		M			dx	11	3,533			,
1 p			EI	dx			1			1	dx	11		EI		,
	0		EI		0		EI							EI		(16.69)
	0				0
		l	M2M p			l M			M					1,5
2 p		l	M2M p	dx		l M		2	M		1 dx	21		1,5	.
2 p			EI	dx				2			1 dx	21		EI	.
		0	EI			0	EI							EI
		0				0

За умовою задачі P0 10 кН циклічна частота змушених коливань

0,9	1 0,9 0,22	EI	0,198	EI	;	(16.70)
		m		m
	2 0,0392	EI .
		m

Для визначення головних коефіцієнтів системи 16. обчислимо величини

1		1	EI	25,4876	,
m 2	m 0,0392		EI	EI
	m 0,0392		m		(16.71)
1		8,4959 .
3m 2		EI

Розв’язання системи алгебраїчних рівнянь

Підставивши всі зазначені величини до 16. і скоротивши на величину EI одержимо остаточно

21,955B1	1,5B2	35,33	0,	(16.72)
1,5B1	1,746B2	15	0.

Розв’язавши систему 16. маємо

B1	2,333;	(16.73)
B2	10,594.

Для перевірки підставимо знайдені величини до сумарного рівняння

20,	455B1 0,246B2 0,246 0;
20,	455 2,333 0,246 10,594 50,33 50,327 50,33 0,003 0.

Рівняння руху мас системи при змушених коливаннях

Амплітуди переміщень мас визначимо за формулами 16.25):

A	B1		B	1	2,333		25, 4876		59,4626		;
1	m	2	1 m 2					EI		EI
	1										(16.74)
											(16.74)
A	B2		B	1		10,594		8, 4959		90,0056 .
2	m	2	2 3m 2					EI		EI
	2

Таким чином рух мас системи при змушених коливаннях відбувається за такими законами

y		59,4626 sin	t,
1		EI
		EI	(16.75)
		90,0056 sin	(16.75)
y	2	90,0056 sin	t.
	2	EI
		EI

обудова навантаженої схеми рами

Перш ніж будувати епюри зусиль необхідно показати всі сили які діють на раму в процесі змушених коливань Така схема амплітудних сил інерції і динамічного навантаження показана на рис 16.5.

2	m1	3	m2 5
2
1		4

Рис 16.5

При побудові схеми спільна для обох мас сила інерції B2 що діє в горизонтальному напрямі розподілена між масами пропорційно їх величинам

B21	m1		B2	2m	10,594	кН		кН
	m1	m2		2m m
								(16.76)
		m2		m
B22			B2		10,594	кН		кН
	m1	m2		2m m

обудова динамічних епюр зусиль
Динамічні епюри зусиль будуються				за формулами			16.	Так для побудови епюри
згинальних моментів необхідно скористатися формулою
		M M1B1 M2 B2 M pP0 .						(16.77)
Процес побудови амплітудної епюри згинальних моментів M								показано на рис 16.2.6.

		4,666	15,891
	3,266	4,666
	3,266
	1,4	15,891	15,891
1,4	1,4
1,4
	Еп M1 B1	15,891	Еп M2B2
		20	33,157
	14		33,157
	14
			24,666
	6	23,296
	6		8,49
6		23,296	Еп M
	Еп Mp P0	23,296
	Еп Mp P0

Рис 16.6

Динамічна епюра Q рис 16. побудована на базі диференціальної залежності з епюрою M :

12,333

7,765

9,409

Еп Q

2,83

Рис 16.7

Q	23,296 7,765 кН;	3 4	8,49	2,83		кН,
1 2	3	3 4	3
	3		3
Q	23,296 33,157 9,409 кН;	3 5	24,666		12,333 кН.
2 3	6	3 5	2
	6		2

Амплітудні поздовжні сили можуть бути обчислені виходячи з рівноваги елементів рами

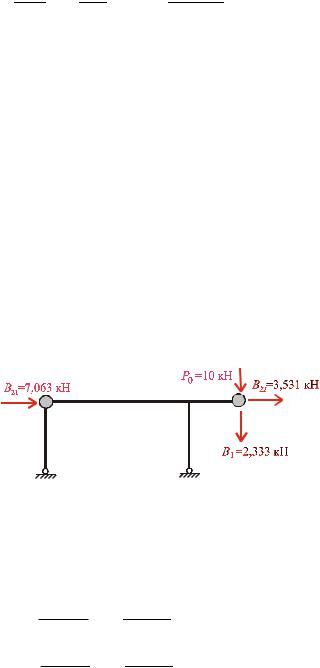
Зумов рівноваги вузла

Fx N2 3 7,063 7,765 0; N2 3 0,702 кН.

Fy N2 1 9,409 0;

N2 1 9,409 кН.

З умов рівноваги стержня -3:

Fx N3 2 N2 3 0;

N3 2 N2 3 0,702 кН.

Зумов рівноваги вузла

Fx N3 5 N3 2 2,83 0; N3 5 3,532 кН.

Fy N3 4 12,33 9,409 0; N3 4 21,739 кН.

Динамічна епюра N поздовжніх сил наведена на рис 16.8.

0,702

9,410

Еп N

21,743

3,533

0,702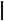

Рис 16.8

Кінематична перевірка розрахунку

Для перевірки порівняємо амплітудні переміщення мас 16. обчислені за формулами (16. з відповідними переміщеннями визначеними за формулою Мора 16.26).

		l	M p1M		dx	6	0 4 1 4,930 2 33,157
1		0		EI	dx	6 2EI	0 4 1 4,930 2 33,157
		0
		1		1 24,666 2 2 2				43,017 16,444		59,461	59,4626 .
	2EI			2		3		EI	EI	EI	EI
		l	M p2M		dx	6		0 4 1,5 4,930 3 33,157
2		0		EI	dx	6 2EI		0 4 1,5 4,930 3 33,157
		0
		1		1 3 3	2 8,49 64,525				25,47 89,995 90,0056 .
	EI			2	3			EI	EI	EI	EI

16.2.3. Розрахунок на змушені коливання розкладанням навантаження по головним формам коливань

Обчислення коефіці нтів розкладення

Для кожної головної форми коливань необхідно за формулою 16.				обчислити коефіцієнт
H j Компоненти зовнішніх навантажень	Pi t	по напрямках можливих переміщень рис 16.1)
мають такі значення
P1 t P0 10 кН;			2 0.
Зведені маси обчислено у співвідношеннях	16.	Величини амплітуд вільних коливань записано
у вигляді векторів 16. і 16.64).

Отже для першої головної форми

		2
		Pi t ai1		P1 t a11					P2 t a21			10 0,263 0			0,8569
H1 i 12				P1 t a11					P2 t a21			10 0,263 0	2		0,8569		.
H1 i 12					m a		2		m a		2	2	2			m	.
			2		m a				m a			m 0,263 3m	1			m
			miai1		1	11			2		21
					1	11			2		21
			i 1
Для другої головної форми
		2
		Pi t ai2		P1	t a12			P2 t a22				10 1 0				9,774
H		i 1		P1	t a12			P2 t a22				10 1 0				9,774		.
H	2	i 1	2			2				2		m 12 3m 0,088		2				.
		miai22			m1a12			m2a22				m 12 3m 0,088				m
		i	1

изначення навантажень відповідних головним формам

Сили відповідні силам інерції головних форм визначаються за формулою 16.27). Для першої головної форми

P11 m1a11H1 m 0,263 0,8569m 0,2254 кН; P21 m2a21H1 3m 1 0,8569m 2,5707 кН.

Для другої головної форми

P12 m1a12 H2 m 1 9,774m 9,774 кН;

P22 m2a22 H2 3m 0.088 9,774m 2,5745 кН.

Виконаємо перевірку розкладення

P1 t P11	P12	0,2254 9,774 9,9994 10;
P2 t P21	P22	2,5707 2,5745 0,0038 0.

обудова епюр від навантажень відповідних головним формам коливань

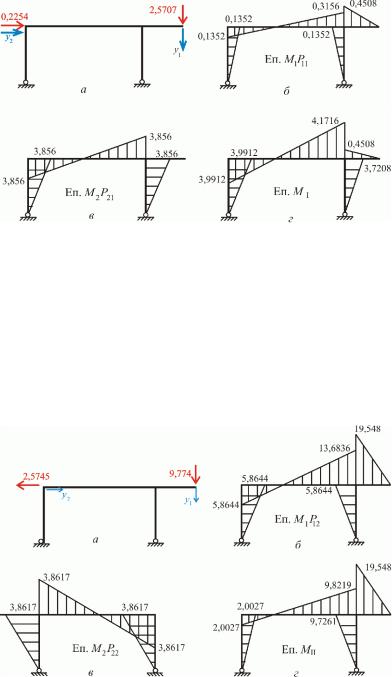
Навантаження відповідне першій головній формі наведено на рис 16.9,а.

Рис 16.9

Епюра згинальних моментів MI від даного навантаження рис 16.9,г може бути побудована за способом накладення

MI M1P11 M2 P21 0,2254M1 2,5707M2 .

рафіки доданків цієї формули побудовано на рис 16.9,б і 16.9,в. Навантаження відповідне першій головній формі наведено на рис 16.10,а.

		Рис 16.10
Епюра згинальних моментів M II		від даного навантаження рис 16.10,г		також може бути
побудована за способом накладення
	MII M1P12	M2 P22 9,774M1 2,5745 M2 .
изначення динамічних кое іцієнтів
За формулою (16.	визначимо	величини динамічних коефіцієнтів для		кожної головної
форми Власні частоти	1, 2 й частота динамічного навантаження		були обчислені раніше
(16.58), (16.70).

									23
			1				1	0,22 2 5,253;
I		1	1 2		1 0,198			0,22 2 5,253;
			1				1	0,564 2 1,140.
II		1	2 2			1 0,198		0,564 2 1,140.
обудова динамічної епюри згинальних моментів
Дійсна динамічна епюра згинальних моментів M								рис 16.11,в	будується як сума епюр від
кожного окремого навантаження які помножені на відповідні динамічні коефіцієнти
			M MI I				MII II .
			21,955						22,285
			21,955					11,197
								11,197
21,006				2,373				2,283
21,006								2,283
21,006						19,582	2,283	11,088
21,006
	Еп M		I					Еп MII II
		I	I
		а						б
		а
			33,152
				24,658
23,289
						8,494
23,289
	Еп M
		в
						Рис 16.11
Епюра згинальних моментів M			побудована шляхом розкладання динамічного навантаження
по головним формам вільних коливань						практично збігається			з епюрою побудованою

безпосереднім розв’язком системи диференціальних рівнянь руху рис 16.6,г Динамічні епюри поперечних Q і поздовжніх N сил можуть бути побудовані так само як в п 16.2.

16.3. иконання розрахунково-графічної роботи з використанням комп’ютерної програми

Розрахунково-графічна робота "Динамічний розрахунок рам" може бути виконана із застосуванням комп’ютерної програми яка входить до програмного навчального комплексу АСИСТЕНТ Програма перевіряє розрахунки виконані "вручну" і в разі відсутності помилок видає результати на принтер або на дисплей Таким чином до роботи на комп’ютері можна приступити лише після закінчення "ручного" розрахунку на вільні та змушені коливання

Для залучення програми до роботи ввести номер схеми і вхідні дані рис 16.12).

Рис 16.12

Програма перевіряє величину найбільшого власного характеристичного числа У разі

помилки програма перевіряє коефіцієнти k матриці податливості кщо старше власне число

обчислено правильно на екран видаються головні форми коливань Для перевірки правильності розрахунку на змушені коливання виконаного вручну програма

пропонує ввести величини амплітудних сил інерції Схема сил показана на рис 16.13.

кН		кН
кН
2	3	5
y		кН
1	4

Рис 16.13

Амплітудні величини сил інерції вводяться у віконця діалогового вікна При цьому сила вважається додатною якщо її напрям збігається з напрямом відповідної координатної осі

кщо сили інерції визначено правильно на екран дисплея видаються амплітудні епюри згинальних моментів поперечних і поздовжніх сил а числові результати виводяться на принтер і додаються до розрахунково-графічної роботи

<<< < Предыдущая 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 4546 / 5346 47 48 49 50 51 52 53 > Следующая >>>

Соседние файлы в предмете Сопротивление материалов

#
28.11.202117.29 Mб112БУДIВЕЛЬНА МЕХАНIКА. Посiбник-2018.pdf
#
29.05.2021266.7 Кб8Приклад Геом переріз.pdf