
- •1. Система сил на площині
- •1.1.Короткі теоретичні відомості
- •1.2. Довільна система сил
- •1.3. Задачі для самоконтролю
- •2. Кінематичний аналіз плоских систем і визначення реакцій з’єднань
- •2.1.Короткі відомості про кінематичний аналіз
- •2.3. Схеми задач для самостійного розв’язування
- •3. Розрахунок плоских статично визначуваних ферм
- •3.1.Короткі теоретичні відомості
- •3.3. Схеми задач для самостійного розв’язування
- •4. Статично визначувані просторові ферми
- •4.1. Короткі теоретичні відомості
- •4.3. Задачі для самостійного розв’язування
- •5. Розрахунок шарнірно-консольної балки на нерухоме навантаження
- •5.1.Основні теоретичні відомості
- •5.3. Задачі для самостійного розв’язування
- •6. Розрахунок тришарнірних арок
- •6.1 Короткі теоретичні відомості
- •6.3. Схеми задач для самостійного розв’язування
- •7. Статично визначувані рами
- •7.1. Короткі теоретичні відомості
- •7.2.Розрахунок простої рами
- •7.3.Розрахунок складеної рами
- •7.4. Розрахунок рами із замкненим контуром
- •8. Розрахунок на рухоме навантаження
- •8.1. Короткі теоретичні відомості
- •8.2. Лінії впливу для двоопорної балки
- •8.3. Лінії впливу для консольної балки
- •8.4. Навантаження ліній впливу
- •8.5. Лінії впливу для шарнірно–консольної балки
- •8.6. Лінії впливу в фермах
- •8.7. Лінії впливу в шпренгельних фермах
- •8.9. Задачі для самостійного розв’язування
- •9. Обчислення переміщень у стержневих системах
- •9.1. Короткі теоретичні відомості
- •9.6. Задачі для самостійного розв’язування
- •10. Розрахунок статично невизначуваної рами методом сил
- •10.1. Короткі теоретичні відомості
- •10.2. Розрахунок рами методом сил
- •10.3. Розрахунок симетричної рами методом сил
- •10.4. Задачі для самостійного опрацювання
- •11. Статично невизначувані ферми
- •11.1.Короткі теоретичні відомості
- •11.3. Задачі для самостійного опрацювання
- •12. Нерозрізна балка
- •12.1.Основні теоретичні відомості
- •12.2. Розрахунок статично невизначуваної балки на постійне навантаження методом трьох моментів
- •12.3.Розрахунок нерозрізної балки на тимчасові навантаження методом моментних фокусів
- •12.5. Задачі для самостійного опрацювання
- •13. Метод переміщень
- •13.1.Короткі відомості про метод переміщень
- •13.2.Розрахунок несиметричної рами в канонічній формі
- •13.3. Розрахунок несиметричної рами в розгорнутій формі
- •13.4. Розрахунок симетричної рами на симетричне навантаження
- •13.6. Задачі для самостійного опрацювання
- •14. Метод скінченних елементів для стержневих систем
- •14.1.Основні положення методу скінченних елементів
- •14.3. Розрахунок шарнірно-стержневої системи методом скінченних елементів
- •14.4. Схеми для самостійного розв’язування
- •15.Розрахунок рам на стійкість
- •15.1. Короткі теоретичні відомості
- •15.3. Розрахунок на стійкість симетричної рами
- •15.4. Задачі для самостійного розв’язування
- •16. Динамічний розрахунок рам
- •16.1.Короткі відомості про розрахунок на динамічні дії
- •16.4. Задачі для самостійного опрацювання
- •17. Розрахунок стінової панелі методом скінченних елементів
- •17.1. Короткі відомості про розрахунок стінової панелі
- •17.3. Задачі для самостійного розв’язування
- •18. Навчальний програмний комплекс АСИСТЕНТ
- •18.1. Основні характеристики
- •18.2. Запуск комплексу АСИСТЕНТ
- •18.3. Керування роботою комплексу
- •18.4. иконання розрахункових робіт
- •19.1. Основні характеристики
- •19.3. Завантаження ОК SCAD і основні елементи керування
- •19.4. Основні етапи створення розрахункової схеми в ОК SCAD

21
При розрахунку за допомогою комп’ютерної програми точки графіка можуть бути знайдені в режимі діалогу з комп’ютером Для цього необхідно під час завдання вхідних даних задавати різні співвідношення зовнішніх сил при фіксованому значенні параметра жорсткості ригеля n.
Приклад введених до комп’ютера співвідношень і відповідні результати наведено в табл 15.11.
Таблиця 15.11
P P |
P P |
Pкр |
Pкр i |
Pкр i |
1 |
2 |
|
1 |
2 |
|
|
|
|
|
0 |
1 |
2,281i |
0 |
2,281 |
|
|
|
|
|
1 |
0 |
1,820i |
1,820 |
0 |
|
|
|
|
|
1 |
1 |
1,243i |
1,243 |
1,243 |
|
|
|
|
|
15.2. .Особливості розрахунку рами на стійкість за допомогою навчальної комп’ютерної програми комплексу АСИСТЕНТ
Комп’ютерна програма з розрахунку рам на стійкість дає можливість автоматизовано вико-
нати більшість розрахунків Для використання програми необхідно вручну виконати перші два етапи скласти рівняння стійкості і обчислити критичне навантаження.
Програма надає можливість в режимі діалогу ввести вхідні дані які стосуються номера заданої схеми геометричних розмірів параметра жорсткості одного або декількох стержнів а також задані співвідношення між зовнішніми силами Для перевірки правильності розрахунків, зроблених вручну програма запропонує ввести критичні величини зовнішніх сил обчислених в п 15. кщо ці результати помилкові програма пропонує ще деякі питання щодо величини критичного параметра навантаження порядку визначника системи рівнянь методу переміщень а також щодо коефіцієнтів і значення визначника обчислених при нульових параметрах стійкості
Наприкінці |
програма повідомить |
місце можливої помилки кщо |
ж |
результати |
розрахунків |
виконаних |
вручну збігаються з |
результатами роботи програми |
то |
вона надає |
можливість |
продовжити роботу в автоматизованому режимі коли можна змінювати будь-які параметри задачі
виконуючи дослідження п п 15. і 15. |
Результати розрахунків можуть бути виведені на екран |
монітора або на принтер |
|
15.3. Розрахунок на стійкість симетричної рами
Схему симетричної рами під дією симетричного вузлового навантаження представлено на рис 15.11,а Необхідно визначити критичну величину вузлових сил
изначення ступеня кінематичної невизначуваності і призначення основної системи
Задана рама має чотири проміжні жорсткі вузли Тому
k 4 7 , |
8 , 4 , 6 . |
22
Рис
Для визначення кількості незалежних поступальних переміщень вузлів утворимо шарнірну
схему рами |
рис 15.11,б Очевидно що |
для перетворення шарнірної |
схеми |
на геометрично |
||||||||||
незмінювану систему необхідно ввести два додаткові опорні стержні |
1 |
та |
2 |
Перший з них |
||||||||||
утримує |
від |
поступального горизонтального |
переміщення |
1 вузли |
|
і |
|
а другий – від |
||||||
поступального горизонтального переміщення |
2 вузли |
і |
На цій підставі вважаємо що |
|||||||||||
|
|
k |
2 |
|
1, |
2 . |
|
|
|
|
|
|
|
|
Поступальні переміщення вузлів визначають кут перекосів стержнів |
|
|
|
|
||||||||||
|
|
1 4 |
|
2 5 |
|
13 6 |
|
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
4 7 |
|
6 8 |
|
1 |
|
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
5 |
|
|
|
|
|
|
|
|
4 6 |
|
5 6 |
|
7 8 0. |
|
|
|
|
|
|
||
Отже ступінь кінематичної невизначуваності рами |
|
|
|
|
|
|
|
|
||||||
|
|
k k |
k 6 . |
|
|
|
|
|
|
|
||||
Основну систему методу переміщень одержимо введенням |
плаваючих |
затиснень у вузли |
||||||||||||
7 , 8 , |
4 , 6 |
задля унеможливлювання |
їхніх |
кутів |
повороту |
а для |
усунення можливих |
|||||||
23
поступальних переміщень – введенням опорних стержнів у вузли |
і |
|
рис 11.5,в). |
||||||||||||||||||||
Епюра N нормальних сил в рамі до настання втрати стійкості подана на рис 11.5,г. |
|||||||||||||||||||||||
Параметри стійкості в стержнях рами виражаються через поздовжні сили |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 7 |
|
N4 7l4 7 |
Ph ; |
|
|
6 8 |
|
N6 8l6 8 |
|
Ph |
|
4 7 ; |
|
||||||||||
|
|
i4 7 |
|
|
i |
|
|
|
|
|
i46 8 |
|
|
|
i |
|
|
|
|
|
|
||
1 4 |
|
N1 4l1 4 |
4Ph |
Ph 4 7 ; |
3 6 |
|
N3 6l3 6 |
|
|
4Ph |
|
|
Ph |
4 7 ; |
|||||||||
|
|
i1 4 |
4i |
i |
|
|
i13 6 |
|
|
|
4i |
|
|
i |
|
||||||||
7 8 |
4 5 5 6 |
2 5 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Симетрична рама під дією симетричного навантаження може деформуватись при втраті стійкості або за симетричною або за кососиметричною формою Реалізуватиметься та форма якій відповідає менше значення критичного навантаження Тому доцільно виконати розрахунок окремо на симетричну і окремо на кососиметричну деформацію
15.3.1. Розрахунок на втрату стійкості за симетричною формою деформації
Очікуваний згин рами при втраті стійкості за симетричною формою деформації показано на рис 15.12.
Рис 15.12
З умов симетрії можна зробити висновки щодо основних невідомих
8 |
|
7 ; |
|
6 |
|
4 ; |
|
1 |
|
2 |
0. |
Таким чином кількість основних невідомих скорочується до трьох При цьому кути перекосу всіх стержнів дорівнюють нулю
1 4 |
4 7 |
2 5 |
6 8 |
3 6 |
7 8 |
4 5 |
5 6 0. |
24
Складання рівнянь рівноваги
Розв’язувальні рівняння складаємо з умов рівноваги елементів які утримуються від переміщень накладеними з’єднаннями ормули для кінцевих зусиль вибираються з табл 5.1, 15. та 15. залежно від граничних умов
M7 M7 4 M7 8 0. |
|
|
|
M 7 4 2i7 4 7 4 |
7 7 4 |
4 7 4 |
7 4 |
2i 7 4 7 7 4 |
4 2i |
7 4 7 2i 7 4 4 ; |
|
M 7 8 2i7 8 2 7 8 2 7 8 2 4i 2 7 7 8i 7 .
|
M 7 2 |
7 4 |
8 i 7 2 7 4i |
4 0. |
|
|
|
(15.35) |
|||
M4 M4 7 M4 5 M4 1 0. |
|
|
|
|
|
||||||
M4 7 |
2i4 7 |
4 7 |
4 4 7 |
7 |
4 7 |
4 7 |
|
||||
2i |
4 7 4 4 7 |
7 2i |
4 7 4 2i 4 7 7 ; |
|
|||||||
M4 5 |
3i4 5 |
4 4 5 3i 4 ; |
|
|
|
|
|
||||
M4 1 i4 1 4 1 |
4 4 1 4i 4 1 4. |
|
|
|
|||||||
|
|
M4 2i |
4 7 |
2 4 7 |
4 4 1 |
3 i 4 |
0. |
|
(15.36) |
||
Складання рівняння стійкості
Умовою втрати стійкості є дорівнювання нулю визначника матриці коефіцієнтів при невідомих переміщеннях вузлів
|
|
2 7 4 |
8 |
2 7 4 |
0 . |
|
|
|
|
|
D |
|
2 4 7 4 4 1 3 |
|
|
||
|
|
2 7 4 |
|
|
|
|
|
|
Розв’язання рівняння стійкості |
|
|
|
|
|
|
||
Відшукаємо перший |
мінімальний корінь рівняння стійкості |
послідовно надаючи одному з |
||||||
параметрів |
який вважатимемо за незалежний нехай це буде параметр |
|
довільних значень |
|||||
наприклад |
тощо |
При кожному значенні незалежного параметра |
|
будемо обчислювати |
||||
відповідні значення інших параметрів знаходити величини функцій , |
, |
за таблицями які |
||||||
наведені в |
Додатках 4 |
і обчислювати |
величину визначника |
Процес |
наближень вважається |
|||
закінченим коли визначник дорівнюватиме нулю |
|
|
|
|
||||
Так взявши маємо з таблиць Додатку 4: |
|
|
|
|
||||

25
|
|
|
|
|
|
7 4 2; |
7 4 |
1. |
|
|
Для |
|
маємо |
|
1 4 |
3 . |
|
|
|
|
|
|
|
|
|
|
|
|||||
Підставивши отримані значення до рівняння стійкості отримаємо |
||||||||||
|
|
|
D |
2 2 8 |
2 1 |
|
12 |
2 |
224. |
|
|
|
|
|
|
2 1 |
2 2 4 3 3 |
2 19 |
|
||
Взявши |
|
маємо |
|
|
|
|
|
|
||
|
|
|
|
|
7 4 |
1,932; |
7 4 |
1,017. |
|
|
Для стержня |
- відповідне значення параметру |
|
|
Маємо з таблиць |
||||||
1 4 2,794.
Тоді
D |
2 |
1,932 8 |
2 |
1,017 |
|
11,864 |
2,034 |
209,9. |
|
2 |
1,017 |
2 |
1,932 4 2,794 3 |
|
2,034 |
18,040 |
|
Продовжуємо аналогічні обчислення надаючи параметру стійкості наступних значень доти поки визначник змінить знак Результати заносимо до таблиці 15.12.
Таблиця 15.12
|
7 4 |
7 4 |
7 4 |
1-4 |
1 4 |
D |
|
|
|
|
|
|
|
1 |
0 |
2 |
1 |
0 |
3 |
224 |
|
|
|
|
|
|
|
2 |
1 |
1,932 |
1,017 |
1 |
2,794 |
209,9 |
|
|
|
|
|
|
|
3 |
2 |
1,718 |
1,076 |
2 |
2,088 |
164,5 |
|
|
|
|
|
|
|
4 |
3 |
1,312 |
1,206 |
3 |
0,408 |
71,3 |
|
|
|
|
|
|
|
5 |
4 |
0,586 |
1,502 |
4 |
-6,518 |
-229,8 |
|
|
|
|
|
|
|
6 |
3,5 |
1,004 |
1,321 |
3,5 |
-1,468 |
-15,6 |
|
|
|
|
|
|
|
7 |
3,4 |
1,073 |
1,294 |
3,4 |
-0,974 |
5,98 |
|
|
|
|
|
|
|
рафік функції D=D( 7-4) побудовано на рис 15.13,а.
D
а
224 |
209,9 |
164,5 |
71,3 |
0 |
1 |
2 |
3 |
3,5 |
4 |
7-4 |
15,6 |
229,8 |
|
5,98 3,4
б
3,5
7-4
15,6
0,1
Рис 15.13
26
к видно визначник D змінює знак при значеннях параметру 1-4 в проміжку між і Виконуючи на означеному проміжку лінійну інтерполяцію (рис 15.13,б) знаходимо
кр |
3,4 |
0,1 5,98 |
3,428. |
4 7 |
5,98 15,6 |
||
|
|
|
Критична величина параметру навантаження при симетричній формі втрати стійкості складає
P |
2 |
i |
|
3,4282 i |
2,350i . |
4 7 |
|
|
|||
кр |
h |
|
|
5 |
|
|
|
|
|
15.3.2. Розрахунок на втрату стійкості за кососиметричною формою деформації
Очікуваний згин рами при втраті стійкості за кососиметричною формою деформації показано на рис 15.14.
Рис 15.14
З умов симетрії можна зробити висновки щодо основних невідомих
8 |
|
7 ; |
6 |
|
4. |
Таким чином кількість основних невідомих скорочується до чотирьох
4 , 7 , 1, 2 . |
|
|
Складання рівнянь рівноваги |
|
|
Розв’язувальні рівняння складаємо з умов |
рівноваги елементів |
які утримуються від |
переміщень накладеними з’єднаннями |
|
|
Так з умов рівноваги вузла |
маємо |
|
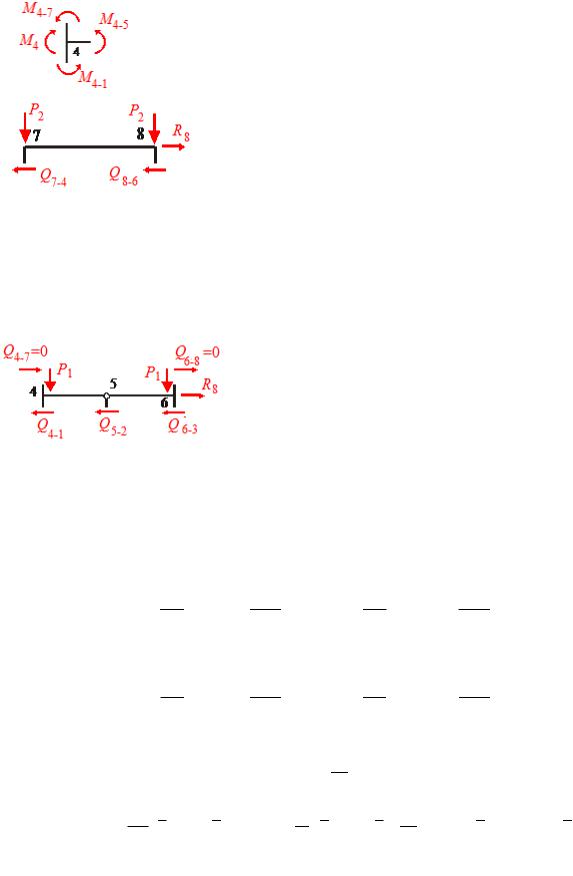
M7 M7 4 M7 8 |
0 . |
(15.37) |
|
|
|
27 |
З умов рівноваги вузла |
|
|
|
M4 |
M4 7 M4 5 |
M4 1 0. |
(15.38) |
З умов рівноваги верхнього ригеля - |
маємо |
||
Fx 0 |
R8 Q7 4 |
Q8 6 0 або R8 |
Q7 4 Q8 6 0 , |
звідки випливає що Q7 4 Q8 6 . |
|
||
З іншого боку внаслідок кососиметричного напружено-деформованого стану рами згинальні
моменти кососиметричні |
а поперечні сили симетричні тобто |
Q7 4 Q8 6 Обидві рівності |
||||||||||||||||||||
можливі лише за умови |
що поперечні сили в стояках дорівнюють нулю |
Q7 4 |
Q8 6 0 |
е |
||||||||||||||||||
означає що поступальне переміщення |
2 |
з числа невідомих можна виключити взявши для |
||||||||||||||||||||
|
|
|
|
|
|
|
стояків |
- |
та |
- формули кінцевих моментів для випадку коли |
||||||||||||
|
|
|
|
|
|
|
поперечна сила дорівнює нулю |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Умова рівноваги нижнього ригеля |
-5- дає |
|
|
|
|||||||||||
|
|
|
|
|
|
|
Fx 0 |
|
|
R7 Q4 1 Q5 2 Q6 3 0 . |
|
|
|
|||||||||
З умов косої симетрії напружено-деформованого стану можна вважати |
що |
Q6 3 Q4 1 |
З |
|||||||||||||||||||
урахуванням отриманого співвідношення умова рівноваги ригеля набуває вигляду |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
R7 2Q4 1 |
Q5 2 |
0 . |
|
|
|
|
|
|
(15.39) |
||||||
Отже виражаємо кінцеві зусилля що входять до рівнянь |
15.37) (15.39). |
|
|
|
||||||||||||||||||
M7 4 i7 4 |
tg |
|
7 |
|
sin |
|
|
4 |
i |
tg |
|
7 |
i |
sin |
|
4 ; |
|
|
|
|||
|
|
7 |
4 |
|
|
7 |
4 |
|
|
7 |
4 |
|
7 |
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
M7 8 2i7 8 2 t |
8 3 7 8 2 4i 2 t 7 24 7 ; |
|
|
|
|
|
|
|
||||||||||||||
M4 7 i7 4 |
tg |
|
4 |
|
sin |
|
|
7 |
i |
tg |
|
4 |
i |
sin |
|
7 ; |
|
|
|
|||
|
|
7 |
4 |
|
|
7 |
4 |
|
|
7 |
4 |
|
7 |
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
M4 5 3i4 5 |
4 4 5 3i 4 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
M4 1 i4 1 4 1 |
4 |
4 1 4i |
4 1 |
4 |
|
1 |
4i 4 1 4 |
0,8i |
4 1 |
1; |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
Q4 1 |
i4 1 |
4 1 |
4 4 1 |
|
4 1 |
4i |
4 |
1 |
4 |
4 1 |
1 |
0,8i |
4 1 |
4 0,16i |
4 1 |
1; |
|
|||||
|
l4 1 |
|
|
|
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
Q5 2 |
3i5 2 |
2 |
|
5 2 |
3 2i |
0 |
1 |
0,24i |
1. |
|
|
|
|
|
|
|
|
|||||
|
l |
|
|
|
|
|
|
5 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

28
Підставивши отримані кінцеві зусилля до системи рівнянь отримаємо систему рівнянь методу переміщень
|
tg |
|
|
24 |
7 |
|
sin |
|
|
4 |
|
|
|
0; |
|
|
7 |
4 |
|
|
|
|
7 4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
sin |
|
|
7 |
|
|
tg |
|
4 1 4 3 |
4 |
0,8 1 4 |
1 |
0; |
(15.40) |
|
|
|
7 |
4 |
|
|
7 |
4 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
0,32 |
4 1 0,24 1 |
|
|
||||
|
|
|
|
|
|
0,8 |
1 4 |
4 |
|
0. |
|
||||
Складання рівняння стійкості
Рівняння стійкості рами одержимо прирівнявши до нуля визначник матриці коефіцієнтів системи рівнянь 15. методу переміщень
|
tg |
7 |
24 |
|
|
sin |
7 |
4 |
0 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||
D |
|
sin |
|
tg |
|
4 |
1 4 3 |
0,8 |
1 4 |
0 |
(15.41) |
|
|
|
7 4 |
7 |
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
1,6 |
1 4 |
|
0,32 4 1 |
0,24 |
|
|
||
Розв’язання рівняння стійкості |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Рівняння стійкості |
15. |
|
|
|
розв’язуємо так само як і для симетричної форми втрати стійкості |
|||||||||||||||||
зважаючи на те |
що 1 4 |
|
4 7 Послідовно надаємо незалежному параметру |
4 7 значень |
і |
|||||||||||||||||
т д Критичною |
буде |
величина |
параметру |
за |
якою визначник 15. |
обертається на |
нуль |
|||||||||||||||
Результати обчислень заносимо в таблицю 15.15. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблиця 15.13 |
|
|||
|
|
|
4 7 |
|
|
|
|
|
|
|
|
|
|
|
|
1-4 |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
1 4 |
1 4 |
|
|
|||||
|
|
|
|
|
tg |
|
4 7 |
|
|
|
4 7 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
0 |
|
|
|
|
1 |
|
|
|
1 |
|
0 |
3 |
3 |
190,8 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
1 |
|
|
0,642 |
|
1,188 |
|
1 |
2,790 |
1,794 |
50,23 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
|
2 |
|
|
-0,915 |
|
2,199 |
|
2 |
2,088 |
-1,911 |
-216,4 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4 |
|
1,2 |
|
|
0,466 |
|
1,287 |
1,2 |
2,699 |
1,259 |
-40,8 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
5 |
|
1,1 |
|
|
0,560 |
|
1,234 |
1,1 |
2,749 |
1,539 |
-30,96 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Виконавши лінійну інтерполяцію в інтервалі |
< |
4-7 < 1,1 знаходимо |
|
|
|
|
||||||||||||||||
