
- •1. Система сил на площині
- •1.1.Короткі теоретичні відомості
- •1.2. Довільна система сил
- •1.3. Задачі для самоконтролю
- •2. Кінематичний аналіз плоских систем і визначення реакцій з’єднань
- •2.1.Короткі відомості про кінематичний аналіз
- •2.3. Схеми задач для самостійного розв’язування
- •3. Розрахунок плоских статично визначуваних ферм
- •3.1.Короткі теоретичні відомості
- •3.3. Схеми задач для самостійного розв’язування
- •4. Статично визначувані просторові ферми
- •4.1. Короткі теоретичні відомості
- •4.3. Задачі для самостійного розв’язування
- •5. Розрахунок шарнірно-консольної балки на нерухоме навантаження
- •5.1.Основні теоретичні відомості
- •5.3. Задачі для самостійного розв’язування
- •6. Розрахунок тришарнірних арок
- •6.1 Короткі теоретичні відомості
- •6.3. Схеми задач для самостійного розв’язування
- •7. Статично визначувані рами
- •7.1. Короткі теоретичні відомості
- •7.2.Розрахунок простої рами
- •7.3.Розрахунок складеної рами
- •7.4. Розрахунок рами із замкненим контуром
- •8. Розрахунок на рухоме навантаження
- •8.1. Короткі теоретичні відомості
- •8.2. Лінії впливу для двоопорної балки
- •8.3. Лінії впливу для консольної балки
- •8.4. Навантаження ліній впливу
- •8.5. Лінії впливу для шарнірно–консольної балки
- •8.6. Лінії впливу в фермах
- •8.7. Лінії впливу в шпренгельних фермах
- •8.9. Задачі для самостійного розв’язування
- •9. Обчислення переміщень у стержневих системах
- •9.1. Короткі теоретичні відомості
- •9.6. Задачі для самостійного розв’язування
- •10. Розрахунок статично невизначуваної рами методом сил
- •10.1. Короткі теоретичні відомості
- •10.2. Розрахунок рами методом сил
- •10.3. Розрахунок симетричної рами методом сил
- •10.4. Задачі для самостійного опрацювання
- •11. Статично невизначувані ферми
- •11.1.Короткі теоретичні відомості
- •11.3. Задачі для самостійного опрацювання
- •12. Нерозрізна балка
- •12.1.Основні теоретичні відомості
- •12.2. Розрахунок статично невизначуваної балки на постійне навантаження методом трьох моментів
- •12.3.Розрахунок нерозрізної балки на тимчасові навантаження методом моментних фокусів
- •12.5. Задачі для самостійного опрацювання
- •13. Метод переміщень
- •13.1.Короткі відомості про метод переміщень
- •13.2.Розрахунок несиметричної рами в канонічній формі
- •13.3. Розрахунок несиметричної рами в розгорнутій формі
- •13.4. Розрахунок симетричної рами на симетричне навантаження
- •13.6. Задачі для самостійного опрацювання
- •14. Метод скінченних елементів для стержневих систем
- •14.1.Основні положення методу скінченних елементів
- •14.3. Розрахунок шарнірно-стержневої системи методом скінченних елементів
- •14.4. Схеми для самостійного розв’язування
- •15.Розрахунок рам на стійкість
- •15.1. Короткі теоретичні відомості
- •15.3. Розрахунок на стійкість симетричної рами
- •15.4. Задачі для самостійного розв’язування
- •16. Динамічний розрахунок рам
- •16.1.Короткі відомості про розрахунок на динамічні дії
- •16.4. Задачі для самостійного опрацювання
- •17. Розрахунок стінової панелі методом скінченних елементів
- •17.1. Короткі відомості про розрахунок стінової панелі
- •17.3. Задачі для самостійного розв’язування
- •18. Навчальний програмний комплекс АСИСТЕНТ
- •18.1. Основні характеристики
- •18.2. Запуск комплексу АСИСТЕНТ
- •18.3. Керування роботою комплексу
- •18.4. иконання розрахункових робіт
- •19.1. Основні характеристики
- •19.3. Завантаження ОК SCAD і основні елементи керування
- •19.4. Основні етапи створення розрахункової схеми в ОК SCAD
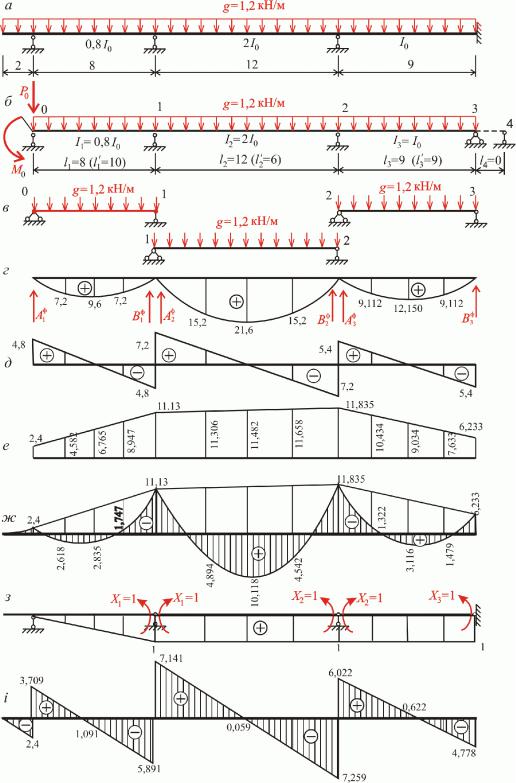
8
12.2. Розрахунок статично невизначуваної балки на постійне навантаження методом трьох моментів
Нерозрізна балка на яку діє рівномірно розподілене навантаження g=1,2 кН/м представлена на рис 12.5,а.
Рис 12.5
9
1.Ступінь статичної невизначуваності
n = 6 – 3 = 3.
ерехід до стандартної схеми балки
При переході до стандартної схеми затиснення на правому кінці балки замінено фіктивним прогоном нульової довжини а консоль на лівому кінці відкинуто Рівномірне розподілене по консолі навантаження замінене зосередженими силою і моментом
P0 1,2 2 2,4 кН; M 0 1,2 2 1 2,4 кНм.
Опори стандартної схеми пронумеровано зліва направо Прогони пронумеровано таким чином щоб номер прогону відповідав номеру його правої опори Прийнявши жорсткість EI0 прогону l3 за основну, визначаємо зведені довжини прогонів
l |
|
EI0 |
|
|
l |
|
|
EI0 |
|
|
8 м 10 м; |
||
|
EI1 |
|
|
|
|
|
|
||||||
1 |
|
|
1 |
0,8EI |
0 |
|
|||||||
l2 |
|
|
EI0 |
l2 |
|
|
EI0 |
12 м 6 м; |
|||||
|
|
|
|
|
|||||||||
|
|
|
EI2 |
|
|
|
|
|
2EI0 |
|
|
|
|
l3 |
|
|
EI0 |
l3 |
|
|
EI0 |
9 м 9 м. |
|||||
|
|
|
|
|
|||||||||
|
|
|
EI3 |
|
|
|
|
|
EI0 |
|
|
|
|
Стандартна схема балки показана на рис 12.5,б.
2.Обчислення фіктивних опорних реакцій
Розглядаючи кожен прогін як балку на двох опорах рис 12.5,в будуємо епюри балкових згинальних моментів Мб і поперечних сил Qб від прогонових навантажень рис 12.5,г і рис 12.5, ) .
Користуючись табл 12. знаходимо фіктивні реакції опор:
|
|
|
|
gl3 |
|
1,2 83 |
||||
A |
B |
|
|
1 |
|
|
|
|
25,6 кНм2 ; |
|
|
|
|
|
|||||||
1 |
1 |
|
24 |
|
24 |
|
|
|
|
|
|
|
|
|
gl3 |
|
1,2 123 |
||||
A |
B |
2 |
|
2 |
|
|
|
|
|
86,4 кНм2 ; |
|
|
|
|
|
||||||
2 |
|
|
24 |
|
24 |
|
|
|
|
|
|
|
|
|
gl3 |
|
1,2 9 |
3 |
|
36,45 кНм2 ; |
|
A |
B |
|
|
3 |
|
|
|
|
||
|
|
|
|
|
||||||
3 |
3 |
|
24 |
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A4 |
B4 |
0. |
|
|
|
|
|
|
||
3.Складання і розв’язування рівнянь трьох моментів |
||||||||||
Складаємо рівняння трьох моментів |
12. |
послідовно для кожної проміжної опори стандартної |
||||||||
схеми балки враховуючи що згинальний опорний момент на крайній лівій опорі дорівнює М0=- 2,4 кНм момент від’ємний оскільки верхні волокна розтягнені а на крайній правій опорі М4=0.
10
Опора |
i= 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
M |
l |
|
2M |
1 |
l |
|
l |
2 |
M |
2 |
l |
2 |
6 B |
l1 |
A |
|
l2 |
|
|
, |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
0 1 |
|
|
|
1 |
|
|
|
|
|
|
1 l |
|
|
|
|
|
2 |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
2,4 10 2M1 10 6 M2 |
6 6 |
25,6 |
10 |
|
|
86,4 |
6 |
|
, |
|
|||||||||||||||||||||||||||||||||||||
|
|
8 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
32M1 6M2 |
426,45. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Опора |
(i = 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
M l |
|
2M |
2 |
l |
2 |
|
l |
3 |
M l |
|
6 B |
l2 |
|
|
|
A |
|
|
l3 |
|
, |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
1 2 |
|
|
|
|
|
|
|
|
3 3 |
|
2 l |
|
|
|
|
|
|
|
3 |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||
M1 6 2M2 6 |
9 M3 9 6 86,4 |
|
6 |
|
|
|
36,45 |
9 |
, |
|
|
|
|
||||||||||||||||||||||||||||||||||
12 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
6M1 30M2 9M3 477,9. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Опора |
|
|
= 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
M |
l |
2M |
3 |
l |
|
l |
4 |
M |
4 |
l |
4 |
6 B |
l3 |
|
|
A |
|
|
|
l4 |
|
, |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
2 3 |
|
|
|
3 |
|
|
|
|
|
|
3 l |
|
|
|
|
|
|
4 |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||
M2 9 2M3 9 |
0 0 6 36,45 |
9 |
|
0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
9M2 18M3 218,7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Отже маємо систему розв’язувальних рівнянь |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32M1 6M 2 |
|
|
|
426,45, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6M1 |
30M 2 9M3 |
477,9, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9M2 |
18M3 |
218,7. |
|||||||||||||
Звідси опорні моменти дорівнюють |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 11,130 кНм, |
|
|
M 2 |
|
|
11,835 кНм, |
M 3 6,253 кНм. |
|||||||||||||||||||||||||||
обудова дійсної епюри моментів рис.12.5,ж)
удуємо епюру опорних моментів |
відкладаючи знайдені опорні моменти над відповідними |
|||
опорами |
рис 12.5,е і |
зєднуючи їх |
прямолінійними |
відрізками Дійсна епюра згинальних |
моментів |
в нерозрізній |
балці отримана додаванням |
епюри опорних моментів рис 12.5,е і |
|
балкових епюр згинальних моментів рис 12.5,г я процедура рівнозначна відкладанню балкових епюр від лінії епюри опорних моментів нколи її називають підвішуванням балкових епюр
11
4. еревірка правильності дійсної епюри згинальних моментів
Для перевірки правильності розрахунку будуємо сумарну одиничну епюру згинальних моментів М рис 12.5, ввівши до заданої схеми три шарніри і приклавши одиничні невідомі моменти водночас в усіх трьох шарнірах Далі маємо за формулою Мора
l |
M M |
dx |
8 |
|
|
0 4 0,5 2,835 1 11,130 |
|
|
|
||||||||||||||
EI |
6 0,8EI |
0 |
|
|
|
||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
1 11,130 4 1 10,118 1 11,835 |
|
9 |
|
1 11,835 |
|||||||||||||||
|
2EI |
|
|
|
|
||||||||||||||||||
|
|
6 |
0 |
|
|
|
|
|
|
|
|
|
|
|
6EI0 |
|
|
|
|||||
4 1 3,116 1 6,233 |
9,100 |
|
17,507 |
|
8,406 |
|
17,506 |
|
17,507 |
0. |
|||||||||||||
|
|
EI0 |
|
|
EI0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
EI0 |
EI0 |
|
|
|
|
EI0 |
||||||
Відносна похибка |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
17,507 17,506 |
100% 0,006% |
1%. |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
17,507 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отже згідно кінематичній перевірці, епюра М правильна
5. изначення поперечних сил
Q0 к 1,2 2 2,4 кН,
Q0-1 |
11,130 2,4 |
4,8 3,709 кН, |
||||||
|
||||||||
|
|
8 |
|
|
|
|
|
|
Q1-0 |
11,130 |
2,4 |
4,8 5,891 кН, |
|||||
8 |
|
|||||||
Q |
|
11,835 |
11,130 |
7,2 7,141 кН, |
||||
|
|
|
|
|||||
1 2 |
|
12 |
11,130 |
|
||||
Q2 1 |
11,835 |
7,2 7,259 кН, |
||||||
12 |
|
|
|
|||||
Q2 3 |
|
6,253 11,835 |
5,4 6,022 кН, |
|||||
6,253 9 11,835 |
|
|||||||
Q3-2 |
5,4 4,778 кН. |
|||||||
|
||||||||
|
|
9 |
|
|
|
|
|
|
Епюра поперечних сил побудована на рис 12.5,
6.Обчислення опорних реакцій
R0 |
3,709 2,4 6,109 кН, |
R2 |
6,022 7,259 13,281 кН, |
R |
7,141 5,891 13,032 кН, |
R |
0 4,448 4,778 кН. |
1 |
|
3 |
|
Перевірка рівноваги (рис 12.6)
Fy 6,109 13,281 13,032 4,778 1,2 2 8 12 9 0.
