
- •1. Система сил на площині
- •1.1.Короткі теоретичні відомості
- •1.2. Довільна система сил
- •1.3. Задачі для самоконтролю
- •2. Кінематичний аналіз плоских систем і визначення реакцій з’єднань
- •2.1.Короткі відомості про кінематичний аналіз
- •2.3. Схеми задач для самостійного розв’язування
- •3. Розрахунок плоских статично визначуваних ферм
- •3.1.Короткі теоретичні відомості
- •3.3. Схеми задач для самостійного розв’язування
- •4. Статично визначувані просторові ферми
- •4.1. Короткі теоретичні відомості
- •4.3. Задачі для самостійного розв’язування
- •5. Розрахунок шарнірно-консольної балки на нерухоме навантаження
- •5.1.Основні теоретичні відомості
- •5.3. Задачі для самостійного розв’язування
- •6. Розрахунок тришарнірних арок
- •6.1 Короткі теоретичні відомості
- •6.3. Схеми задач для самостійного розв’язування
- •7. Статично визначувані рами
- •7.1. Короткі теоретичні відомості
- •7.2.Розрахунок простої рами
- •7.3.Розрахунок складеної рами
- •7.4. Розрахунок рами із замкненим контуром
- •8. Розрахунок на рухоме навантаження
- •8.1. Короткі теоретичні відомості
- •8.2. Лінії впливу для двоопорної балки
- •8.3. Лінії впливу для консольної балки
- •8.4. Навантаження ліній впливу
- •8.5. Лінії впливу для шарнірно–консольної балки
- •8.6. Лінії впливу в фермах
- •8.7. Лінії впливу в шпренгельних фермах
- •8.9. Задачі для самостійного розв’язування
- •9. Обчислення переміщень у стержневих системах
- •9.1. Короткі теоретичні відомості
- •9.6. Задачі для самостійного розв’язування
- •10. Розрахунок статично невизначуваної рами методом сил
- •10.1. Короткі теоретичні відомості
- •10.2. Розрахунок рами методом сил
- •10.3. Розрахунок симетричної рами методом сил
- •10.4. Задачі для самостійного опрацювання
- •11. Статично невизначувані ферми
- •11.1.Короткі теоретичні відомості
- •11.3. Задачі для самостійного опрацювання
- •12. Нерозрізна балка
- •12.1.Основні теоретичні відомості
- •12.2. Розрахунок статично невизначуваної балки на постійне навантаження методом трьох моментів
- •12.3.Розрахунок нерозрізної балки на тимчасові навантаження методом моментних фокусів
- •12.5. Задачі для самостійного опрацювання
- •13. Метод переміщень
- •13.1.Короткі відомості про метод переміщень
- •13.2.Розрахунок несиметричної рами в канонічній формі
- •13.3. Розрахунок несиметричної рами в розгорнутій формі
- •13.4. Розрахунок симетричної рами на симетричне навантаження
- •13.6. Задачі для самостійного опрацювання
- •14. Метод скінченних елементів для стержневих систем
- •14.1.Основні положення методу скінченних елементів
- •14.3. Розрахунок шарнірно-стержневої системи методом скінченних елементів
- •14.4. Схеми для самостійного розв’язування
- •15.Розрахунок рам на стійкість
- •15.1. Короткі теоретичні відомості
- •15.3. Розрахунок на стійкість симетричної рами
- •15.4. Задачі для самостійного розв’язування
- •16. Динамічний розрахунок рам
- •16.1.Короткі відомості про розрахунок на динамічні дії
- •16.4. Задачі для самостійного опрацювання
- •17. Розрахунок стінової панелі методом скінченних елементів
- •17.1. Короткі відомості про розрахунок стінової панелі
- •17.3. Задачі для самостійного розв’язування
- •18. Навчальний програмний комплекс АСИСТЕНТ
- •18.1. Основні характеристики
- •18.2. Запуск комплексу АСИСТЕНТ
- •18.3. Керування роботою комплексу
- •18.4. иконання розрахункових робіт
- •19.1. Основні характеристики
- •19.3. Завантаження ОК SCAD і основні елементи керування
- •19.4. Основні етапи створення розрахункової схеми в ОК SCAD
11
Другий етап. Для встановленої в небезпечне положення системи сил обчислюється величина шуканого фактора Sk за формулою 8. е й буде його найбільше за величиною значення.
8.5. Лінії впливу для шарнірно–консольної балки
Для побудови ліній впливу шарнірно–консольну балку доцільно представити у вигляді
сукупності однопрогонових балок які мають або одну опору затиснення |
або дві шарнірні |
|||||||
опори одна |
з яких шарнірно-нерухома а друга |
шарнірно-рухома |
Кожна |
з |
таких |
|||
однопрогонових балок спирається або на основу |
або на інші прості балки |
Утворена схема |
||||||
називається |
поверховою |
де кожна однопрогонова балка розглядається як окремий |
поверх |
|||||
конструкції |
ільш докладно утворення |
поверхових" схем балок розглядається в главі |
|
|
||||
Побудова |
ліній впливу |
будь яких |
факторів |
які |
виникають в шарнірно-консольній |
балці |
||
виконується за два етапи
1.За звичайними правилами будується лінія впливу лише для однопрогонової балки до якої відноситься фактор що аналізується
2.Побудована лінія впливу послідовно продовжується на однопрогонові балки сусідніх
"поверхів" в такий спосіб щоб на кожному поверсі вона по–перше була прямолінійною, і по–друге перетинала вісь балки на віддаленій опорі "поверху".
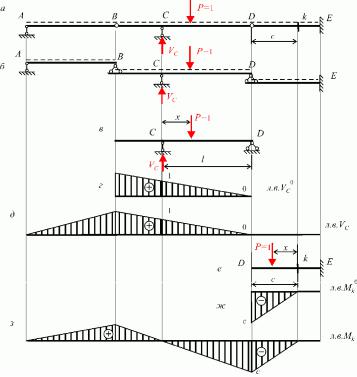
Розглянемо побудову ліній впливу для шарнірно–консольної балки представленої на рис 8.6,а.
Рис 8.6
12
обудова поверхової схеми шарнірно–консольної балки
арнірно-консольну балку ABCDE можна представити як сукупність трьох однопрогонових балок AB, BCD і DE які спираються одна на одну Перший поверх – це консольна балка DE яка безпосереднє спирається на основу Другий поверх – це двоопорна балка BCD яка спирається на поверх DE Третій – це двоопорна балка AB яка спирається на балку другого поверху "Поверхова" схема зображена на рис 8.6,б.
обудова лінії впливу опорної реакції VC |
|
||
Реакція відноситься для двоопорної балки поверху |
BCD рис 8.6,в) Тому на першому |
||
етапі будуємо лінію впливу опорної реакції VC саме для цієї балки |
|||
M D 0 |
VC l 1 l x 0 |
VC l x VC x . |
|
|
|
|
l |
Прямолінійний графік функції VC x |
лінію впливу опорної реакції VC0 для двоопорної балки |
||
поверху BCD проведемо через значення функції в двох довільних точках |
|||
x 0 |
VC 0 l |
1; |
|
|
l |
|
|
x l |
VC l l l 0. |
|
|
|
|
l |
|
Лінія впливу опорної реакції VC для двоопорної балки поверху BCD побудована на рис 8.6,г. Другий етап Подовжуємо лінію впливу на "поверх" AB по прямій яка перетинає вісь на опорі А Надалі продовжимо лінію впливу опорної реакції VC на "поверх" DE по прямій яка перетинає
вісь на опорі E Остаточна лінію впливу опорної реакції VC представлена на рис 8.6, .
обудова лінії впливу згинального моменту Mk
Переріз k шарнірно–консольної балки розташований на консольній балці першого "поверху"
DE рис 8.6,е).
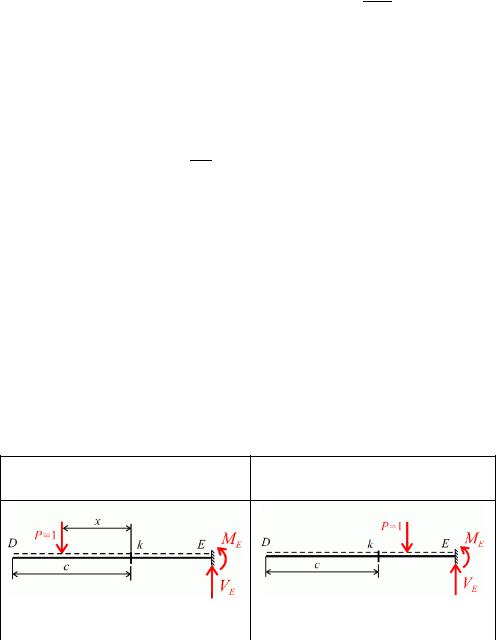
ерший етап Визначаємо згинальний момент Mk у перерізі k балки DE розглядаючи два випадки розташування сили ліворуч і праворуч перерізу k.
Сила P=1 ліворуч перерізу k |
Сила P=1 праворуч перерізу k |
Mk |
Mk |
1 x. |
Mk |
Mk |
0. |
|
л в |
|
|
л в |
|
13
(при x=0 Mk(0)=0 при x=c Mk(c)=-c)
рафік функції Mk x для балки першого "поверху" DE побудовано на рис 8.6, .
Другий етап. Подовжуємо побудований графік на балку другого поверху BCD На протязі всього поверху проводимо прямолінійний відрізок який перетинає вісь балки на опорі . Далі подовжимо графік на перший поверх АВ як прямий відрізок який має нульову ординату на опорі А Остаточна лінія впливу згинального моменту Mk наведена на рис 8.6, .
8.6. Лінії впливу в фермах
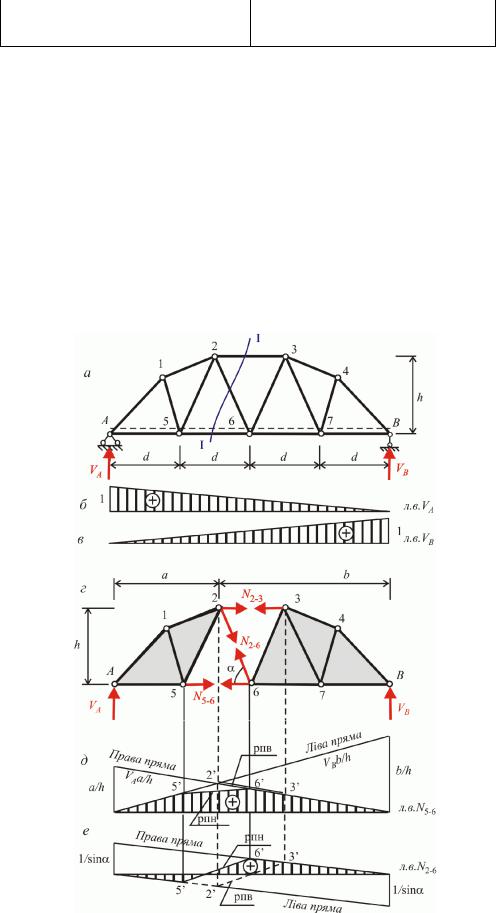
Лінії впливу опорних реакцій в фермах аналогічні лініям впливу опорних реакцій в балках Так для ферми представленій на рис 8.7,а лінії впливу опорних реакцій наведено на рис 8.7,б та
8.7,в.
Рис 8.7
14
Для визначення поздовжніх сил в стержнях ферми використовуються ті ж самі методи що й для дії нерухомих сил Проте, на відміну від балки, необхідно заздалегідь визначити по якому поясу ферми рухається одинична сила е пов’язано з тим що для деяких стержнів лінії впливу зусиль при русі сили по верхньому і по нижньому поясу ферми відрізняються одна від одної.
Метод наскрізних перерізів
Застосуємо метод наскрізних перерізів для аналізу поведінки зусиль в стержнях N5 6 та N2 6 .
Переріз – який перетинає обидва зазначені стержні поділяє ферму на два окремі диски рис8.7,г Замість розрізаних стержнів прикладаємо поздовжні сили N5 6 , N2 6 , N2 3 які
спрямовуються в додатних напрямах тобто від відповідних вузлів |
удемо вважати що одинична |
|||||||
сила переміщується по нижньому поясу ферми |
рух по низу |
В опорах виникають вертикальні |
||||||
опорні реакції VA x ,VB x |
графіки зміни яких |
лінії впливу побудовано на рис 8.7,б та 8.7,в. |
||||||
Для зусилля N5 6 існує моментна точка точка Ріттера |
яка розташована у місці перетину двох |
|||||||
інших зусиль тобто у вузлі |
Тому для визначення зусилля |
N5 6 |
необхідно скласти рівняння |
|||||
моментів щодо цього вузла |
о стосується зусилля N2 6 |
то тут моментної точки не існує бо два |
||||||
інші зусилля паралельні між собою |
Тому для визначення |
зусилля N2 6 |
необхідно |
скласти |
||||
рівняння проекцій на вертикальну вісь |
|
|
|
|
|
|
|
|
к для визначення зусилля N5 6 |
так і для визначення зусилля N2 6 необхідно розглядати |
|||||||
рівновагу того диска на який діє менша кількість сил |
Зважаючи на те |
що одинична сила |
||||||
рухається і в процесі руху може перебувати як на лівому |
так і на правому дисках |
будемо |
||||||
розглядати обидва можливі випадки |
Причому |
якщо сила перебуває на лівому диску |
будемо |
|||||
аналізувати рівновагу правого диска а якщо перебуває на правому диску то – рівновагу лівого
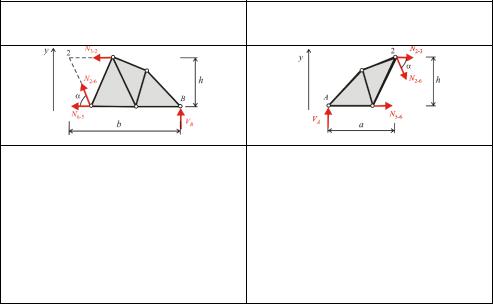
Сила P=1 на лівому диску |
Сила P=1 на правому диску |
M2 0 |
|
|
|
N6 5h VBb 0 , |
M2 0 |
|
|
|
|
N5 6h VAa 0 , |
||||||
|
|
N |
6 5 |
b V |
|
|
N |
5 6 |
a V |
|
. |
|
||||
|
|
|
|
h |
B |
|
|
|
|
h |
A |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Fy 0 |
|
|
|
N6 2 sin |
VB 0, |
Fy 0 |
|
|
|
N2 6 |
sin VA 0, |
|||||
N |
6 |
2 |
|
1 V . |
|
N |
2 |
6 |
1 |
V |
. |
|||||
|
|
|
sin |
B |
|
|
|
sin |
|
A |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

15
Отже в межах лівого диска лінія впливу зусилля N5 6 може бути побудована множенням лінії
впливу опорної реакції V на коефіцієнт b |
це буде так звана ліва пряма |
а в межах правого |
|||||
B |
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диска – множенням лінії впливу опорної реакції V на коефіцієнт a |
права пряма |
|
|
||||
|
|
A |
h |
|
|
|
|
|
|
|
|
|
|
|
|
Ліва пряма штрихується в межах лівого |
а права – в межах правого диска рис 8.7, |
кщо |
|||||
одинична сила перебуває на нижньому поясі |
ліва пряма штрихується на ділянці А – |
а права – |
|||||
на ділянці – В. У межах розрізаної панелі нижнього поясу ферми 5–6 |
ліва і права прямі |
||||||
з’єднуються прямим відрізком який називається передатною прямою або зрізкою. |
кщо ж рух |
||||||
здійснюється по верхньому поясу то ліва пряма штрихується на ділянці А – 2 а права – на ділянці 3 – В . Аналогічно, ліва й права прямі в межах розрізаної панелі верхнього поясу ферми 2– 3 з’єднуються передатною прямою Таким чином лінія впливу має дві передатні прямі одна для руху по верхньому а інша – для руху по нижньому поясу ферми Слід звернути увагу на те що ліва й права прямі перетинаються під моментною точкою
Так само будується лінія впливу зусилля N2 6 У межах лівого диска лінія впливу опорної
реакції V множиться на коефіцієнт 1 |
це буде ліва пряма а в межах правого диска – |
||
B |
sin |
|
|
|
|
|
|
множенням лінії впливу опорної реакції V |
на коефіцієнт 1 |
права пряма Ліва і права прямі |
|
|
A |
sin |
|
|
|
|
|
паралельні Вони не перетинаються що відповідає відсутності моментної точки Ліва пряма штрихується в межах лівого а права – в межах правого вантажного поясу диска
рис 8.7,е Так якщо одинична сила перебуває на нижньому поясі ліва пряма штрихується на ділянці А – а права – на ділянці – В У межах розрізаної панелі нижнього поясу ферми 5–6 ліва і права прямі з’єднуються передатною прямою кщо ж рух здійснюється по верхньому поясу то ліва пряма штрихується на ділянці А – 2 а права – на ділянці 3 – В . Аналогічно, ліва і права прямі в межах розрізаної панелі верхнього поясу ферми 2–3 з’єднуються передатною прямою Отже лінія впливу також має дві передатні прямі одна для руху по верхньому а інша – для руху по верхньому поясу ферми
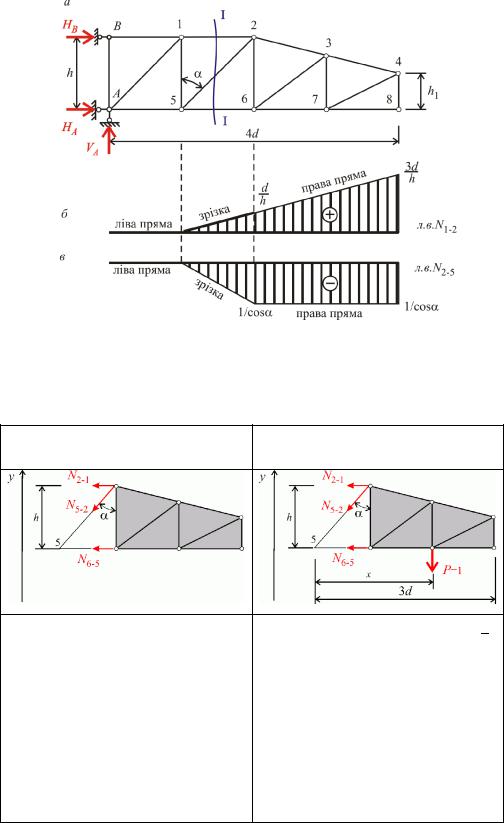
Для визначення зусиль в стержнях консольних систем опорні реакції визначати не обов’язково бо при розрахунку зусиль методом наскрізних перерізів можна завжди обмежитись аналізом рівноваги консольної частини Побудуємо наприклад лінії впливу зусиль в стержнях – та – консольної ферми рис 8.8,а).
16
Рис 8.8
Проводимо переріз – який поділяє ферму на два диска і розглянемо рівновагу правого диска для обох випадків розташування рухомої сили сила на лівому диску та сила на правому диску
Сила P=1 на лівому диску |
Сила P=1 на правому диску |
M5 0 |
N2 1h 0 |
N2 1 0. |
M5 |
0 N2 1h 1 x 0 |
|
N2 1 |
x |
. |
||
|
|
|
|
h |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При x d |
N2 1 d |
d |
|
|
||
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
При x d |
N2 1 d |
|
3d |
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
||
Fy 0 |
N5 2 cos 0 |
N5 2 0. |
Fy |
0 N5 2 cos |
1 0 |
|
|
|
||
|
|
|
|
N5 2 |
|
1 . |
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
Для обох ліній впливу ліві прямі |
прямі в межах лівих дисків збігаються з базовою лінією |
Права пряма лінії впливу N2 1 є похилою прямою а на лінії впливу зусилля N5 2 – права пряма |
|
паралельна базовій лінії к і раніше |
зрізки передатні прямі) з’єднують ліві і праві прямі в |
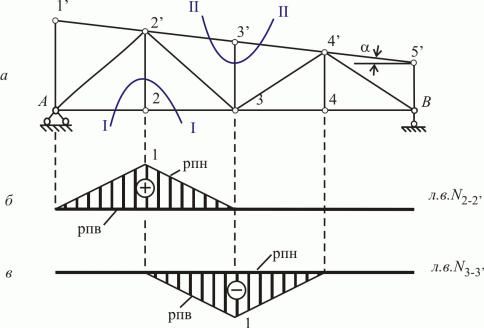
17
межах розрізаної панелі вантажного поясу ферми Остаточні лінії впливу побудовано на рис 8.8,б
та 8.8,в.
Таким чином лінія впливу побудована способом наскрізних перерізів складається з трьох прямих
1.Ліва пряма яка перетинає вісь на лівій опорі і штрихується в межах вантажного поясу лівого диска
2.Права пряма що перетинає вісь на правій опорі і штрихується в межах вантажного поясу правого диска Ліва й права прямі завжди перетинаються під моментною точкою
3.Передатна пряма з’єднує ліву й праву прямі в межах розрізаної панелі вантажного поясу
ферми |
ноді передатна пряма може збігатися з лівою чи правою прямою |
|||
Метод вирізання вузлів |
|
|||
Метод застосовується у випадку |
коли можна замкненим перерізом вирізати вузол ферми і |
|||
скласти для нього рівняння проекцій |
яке міститиме лише одну невідому величину – зусилля в |
|||
стержні |
що |
аналізується Рівняння |
проекцій складається для двох випадків розташування |
|
одиничної сили |
сила розташована поза вузлом тобто за межами панелей які розсікаються при |
|||
вирізанні вузла |
і сила знаходиться у вузлі |
|||
Для |
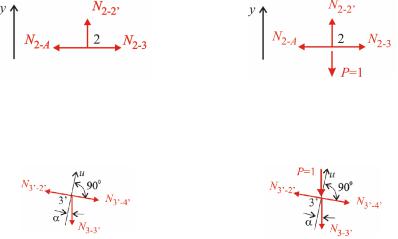
прикладу побудуємо лінії впливу зазначеним методом для стержнів –2' та –3' |
|||
(рис 8.9,а).
Рис 8.9
18
Перерізами – і – вирізаємо вузли та відповідно Далі для кожного вузла складаємо рівняння проекцій вибираючи для проецирування вісь в такий спосіб щоби на неї проецирувалось лише одне невідоме – зусилля в стержні що аналізується
|
|
Сила P=1 поза вузлом 2 |
|
|
Сила P=1 у вузлі |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fy 0 |
N2 2 0. |
|
Fy 0 |
N2 2 1 0 |
N2 2 |
1. |
|
|
|
|
|
Сила P=1 поза вузлом 3' |
|
Сила P=1 у вузлі |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fu 0 |
N3 3 0. |
|
Fu 0 |
|
N3 3 cos |
1 cos |
0. |
|
|
|
|
|
|
|
|
|
N3 3 1 . |
|
|
|
|
|
|
|
|
|
|
||||||
к випливає з розрахунку зусилля N2 2' |
поза вирізаним вузлом |
тобто за межами розрізаних |
|||||||||
панелей А- та |
- дорівнює нулю а в самому вузлі дорівнює одиниці |
Тому на розрізаних |
|||||||||
панелях необхідно провести передатні прямі що з’єднують одиничну ординату у вузлі |
з нулями |
||||||||||
у вузлах А та |
е й буде лінія впливу зусилля N2 2' |
Причому оскільки в процесі розрахунку |
|||||||||
розглядалось розташування одиничної сили у вузлі нижнього поясу це графік для руху |
по низу |
||||||||||
кщо ж сила рухається по верхньому поясу то вона не може потрапити у вузол Тому лінія впливу зусилля N2 2' буде нульовою рис 8.9,б).
Аналогічно будується лінія впливу зусилля N3 3' рис 8.9,в Проте в цьому випадку одиничне значення у вирізаному вузлі відповідає руху сили по верхньому а нульове – по нижньому поясу
Метод сумісних перерізів
Метод застосовують для визначення зусиль у стержнях які неможливо обчислити за способами вирізання вузлів і наскрізних перерізів дея методу полягає в тому що шукане зусилля виражається через інше яке можна знайти способом вирізання вузлів або способом наскрізних перерізів
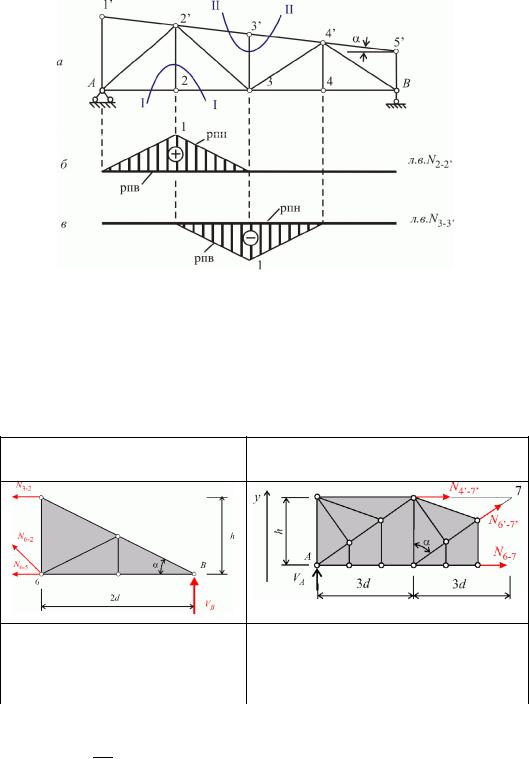
Побудуємо наприклад лінію впливу зусилля в стержні N3 6 рис 8.10,а).
19
Рис 8.10
Лінії впливу опорних реакцій показано на рис 8.10,б та рис 8.10,в.
к допоміжну побудуємо лінію впливу зусилля N2 3 використовуючи метод наскрізних перерізів Переріз – поділяє ферму на два незалежних диска Визначимо зусилля N2 3 для двох випадків розташування одиничної сили сила на лівому і сила на правому диску
Сила P=1 на лівому диску |
Сила P=1 на правому диску |
|
M6 0 |
N3 2h VB 2d 0 |
M6 |
0 N2 3h VA 2d 0 |
|
|
|||||||
|
|
N |
3 2 |
|
2d V . |
|
N |
2 3 |
2d V |
. |
|
|
|
|
|
|
|
h |
B |
|
|
h A |
|
|
|
||
|
|
|
|
||||||||||
Лінія впливу зусилля в стержні N3 6 |
будується шляхом множення ліній впливу опорних |
||||||||||||
реакцій на коефіцієнт |
2d |
рис 8.10,г |
Ліва пряма штрихується в межах лівого |
а права – в |
|||||||||
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
межах правого диска |
Зрізка передатна пряма), яка в межах розрізаної панелі з’єднує ліву та |
||||||||||||
праву прямі розташована на лівій прямій |
|
|
|
|
|
|
|
||||||
Далі проводимо переріз |
– |
який виокремлює вузол |
і складаємо рівняння рівноваги для |
||||||||||
двох випадків сила P 1 поза вузлом тобто за межами розрізаних стержнів – та |
– та сила |
||||||||||||
P 1 у вузлі |
|
|
|
|
|
|
|
|
|
|
|
|
|
