8
Fx |
14,55 4,95 4 4 0,6 0. |
Fy |
9,4 3,4 4 4 0,8 0. |
MC 3,4 5 3 12 4 4 2 0.
7.3.Розрахунок складеної рами
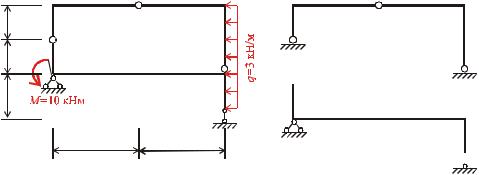
Схема рами на яку діє рівномірно розподілене навантаження і зосереджений момент представлено на рис 7.3,а Необхідно виконати статичний розрахунок рами тобто побудувати епюри згинальних моментів M поперечних сил Q i поздовжніх сил N
|
а |
E |
|
б |
E |
|
|
|
|
||
2 |
C |
|
|
C |
|
|
|
|
|
||
2 |
A |
|
D |
в |
D |
|
|
|
|||
2,4 |
|
|
|
C |
|
|
|
B |
A |
D |
|
|
|
|
|||
|
|
5 |
5 |
|
|
B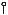
|
Рис 7.3 |
|
Кінематичний аналіз |
|
|
Рама складається з чотирьох дисків AB, CE, ED і |
основа які з’єднані між собою |
|
шарнірами C, E, D і кінематичними в’язями в опорах А і |
Таким чином для проведення |
|
кількісного етапу кінематичного аналізу рами маємо |
|
|
кількість простих дисків D = 4; |
|
|
кількість вузлів в’язей В = 0; |
|
|
кількість простих припайок П = 0; |
|
|
кількість простих шарнірів |
= 3; |
|
кількість кінематичних в’язей |
= 3. |
|
Ступінь геометричної змінюваності
3 4 0 0 2 3 3 3 0 .
Зточки зору геометричної структури доходимо висновку що рама є складеною Дійсно процес її утворення має два етапи на першому етапі диск AB приєднується до основи трьома кінематичними в’язями які не перетинаються в спільній точці і водночас всі три не паралельні
між собою Таке поєднання дисків утворює новий диск диск першого |
поверху На другому |
етапі до диску першого поверху приєднуються диски CE і ED |
таким чином що три |
9
зазначені диски утворюють шарнірний трикутник в якому всі три шарніри не розташовані на одній прямій Отже зазначена схема утворює собою єдиний диск і є геометрично незмінюваною Процес утворення схеми можна записати у вигляді послідовності формул
1. |
DAB |
Dземля |
|
I . |
A1, |
A2,CB |
|
||
|
|
|
||
|
DCE |
DDE |
I |
|
2. |
|
|
|
II . |
|
, D , |
|
||
|
|
E |
||
Перший поверх заданої рами показано на рис 7.3,в другий на рис 7.3,б.
Розрахунок складеної рами тобто визначення реакцій і обчислення внутрішніх зусиль будемо виконувати для кожного поверху окремо починаючи з другого поверху Згодом знайдені зусилля відкладемо на повній схемі складеної рами
Розрахунок рами другого поверху
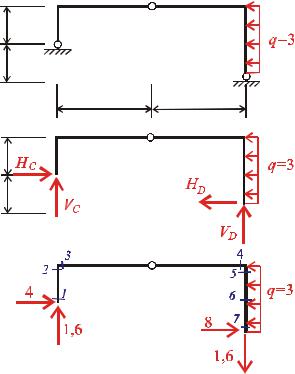
Схема рами другого поверху наведено на рис 7.4,а.
|
а |
E |
|
|
|
2 |
K |
F |
C |
|
|
|
|
|
2 |
|
D |
55
бE
2
C |
D |
2 |
|
в
Рис 7.4
Визначимо реакції опор другого |
поверху |
рис 7.4,б з умов його рівноваги |
||
M D 0 |
VC 10 HC 2 3 4 2 0 |
10Vc 2HC 24 0, |
||
л в |
0 |
VC 5 HC 2 0 |
5VC |
2HC 0. |
M E |
||||
10
Розв’язавши систему двох рівнянь знаходимо
VC 1,6 кН, |
HC 4 кН. |
|
|
|
|
|
|
|
|
Аналогічно |
|
|
|
|
|
|
|
|
|
MC 0 |
VD 10 HD 2 0 |
10VD 2HD 0, |
|
|
|||||
|
рав 0 |
V 5 H |
|
4 3 4 2 0 |
5V |
4H |
|
24 0. |
|
M |
D |
D |
|||||||
|
E |
D |
|
|
D |
|
|
||
Розв’язання отриманої системи двох рівнянь дає
VD 1,6 кН, H D 8 кН .
Перевірка рівноваги рами CED:
Fx 4 8 3 4 0, |
|
|
|
Fy 1,6 |
1,6 0. |
Розіб’ємо схему поверху на три ділянки незважаючи на наявність шарніра ригель розглядаємо як одну ділянку і позначимо перерізи для обчислення зусиль рис 7.4,в).
Обчислимо згинальні моменти
|
ни |
0, |
|
|
|
M1 M1 |
|
|
|||
|
ни |
4 2 8 кНм, |
розтяг ліворуч |
||
M |
2 M 2 |
||||
|
л в |
4 2 8 кНм, |
розтяг зверху |
||
M 3 M 3 |
|||||
|
л в |
4 2 1,6 10 8 кНм, розтяг знизу |
|||
M |
4 M 4 |
||||
|
ни |
8 4 3 4 2 8 кНм, |
розтяг ліворуч |
||
M 5 M 5 |
|||||
|
ни |
8 2 3 2 1 10 кНм, |
розтяг ліворуч |
||
M |
6 M 6 |
||||
|
ни |
0. |
|
|
|
M |
7 M 7 |
|
|
||
Поперечні сили |
|
|
|||
|
|
ни |
4 кН, |
|
|
Q1 Q2 Fn,1 |
|
|
|||
|
|
л в |
1,6 кН, |
|
|
Q3 Q4 Fn,3 |
|
|
|||
|
ни |
8 3 4 1,6 кН, |
|
|
|
Q5 Fn,5 |
|
|
|||
|
ни |
8 кН. |
|
|
|
Q7 Fn,7 |
|
|
|||
11
Поздовжні сили
N1 N2 Ftни,1 N3 N4 Ftл,2в N5 N7 Ftни,5
1,6 кН,
4 кН,
1,6 кН.
Розрахунок рами першого поверху
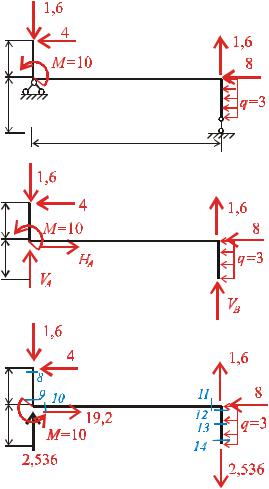
Схема рами першого поверху показана на рис 7.5,а Опорні реакції другого поверху прикладено як вже відомі зовнішні сили
|
C |
а |
|
|
|
2 |
|
D |
|
|
A |
2,4 |
|
B |
|
|
10 |
б
2
|
2,4 |
A |
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
в |
|
|
|
2 A |
|
|
|
|
2,4 |
|
|
|
|
|
|
B |
|
|
|
Рис 7.5 |
|
|
Визначимо реакції опор першого поверху |
рис 7.5,б з умов його рівноваги |
|||
Fx 0 |
HA 4 8 3 2,4 0 |
HA 19,2 кН, |
|
|
M A 0 |
VB 10 4 2 1,6 10 3 2,4 1,2 10 0 |
VB 2,536 кН, |
||
Fy 0 |
VA 2,536 1,6 1,6 0 |
VA 2,536 кН. |
|
|
Розіб’ємо схему поверху на три ділянки і позначимо перерізи для обчислення зусиль рис 7.5,в).
12
Обчислимо згинальні моменти
вер |
0, |
|
|
M 8 M 8 |
|
|
|
вер |
4 2 8 кНм, розтяг праворуч |
||
M 9 M 9 |
|||
л в |
4 2 10 18 кНм, |
розтяг зверху |
|
M10 M10 |
|||
M11 M11рав 3 2,4 1,2 8,64 кНм, |
розтяг зверху |
||
л в |
3 2,4 1,2 8,64 кНм, |
розтяг праворуч |
|
M12 M12 |
|||
ни |
3 2,4 1,2 8,64 кНм, |
розтяг зверху |
|
M13 M13 |
|||
ни |
0. |
|
|
M14 M14 |
|
||
Поперечні сили |
|
|
|
|
вер |
4 кН. |
|
Q8 Q9 Fn,8 |
|
||
|
л в |
2,536 1,6 0,936 кН. |
|
Q10 Q11 Fn,10 |
|||
ни |
3 2,4 7,2 кН. |
|
|
Q12 Fn,12 |
|
||
ни |
0. |
|
|
Q14 Fn,14 |
|
|
|
Поздовжні сили |
|
|
|
|
вер |
1,6 кН. |
|
N8 N9 Ft ,8 |
|
||
|
л в |
4 19,2 15,2 кН. |
|
N10 N11 Ft ,10 |
|||
|
ни |
4 19,2 15,2 кН. |
|
N12 N14 Ft ,12 |
|||
Епюри згинальних моментів М поперечних сил Q і поздовжніх сил N побудовано на рис 7.7.
13
а
8
8 |
8 |
|
|
||
|
8 |
|
18 |
10 |
|
|
8,64 |
|
8 |
8,64 |
|
2,16 |
||
M |
||
|
||
б |
|
|
1,6 |
1,6 |
|
4 |
4 |
|
0,836 |
7,2 |
|
4 |
||
8 |
||
|
||
Q |
|
|
в |
|
|
1,6 |
1,6 |
|
|
||
4 |
4 |
|
15,2 |
15,2 |
|
1,6 |
1,6 |
|
2,536 |
||
|
||
N |
2,536 |
Рис 7.6
еревірки епюр
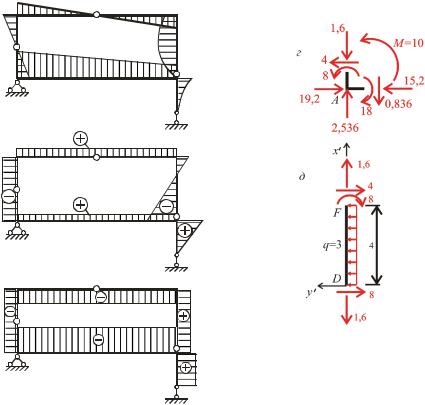
Перевіримо рівновагу одного з вузлів наприклад вузла A Вирізаний вузол зображено на рис 7.7.,г До вузла в місцях розрізів прикладено внутрішні зусилля які вибираються з епюр Згинальні моменти які на епюрі М відкладено зверху прикладаються так щоб зумовлювати розтяг верхніх волокон Додатну поперечну силу на ригелі спрямовано так що вона намагається повернути вузол за годинниковою стрілкою а від’ємна поперечна сила на стояку – проти годинникової стрілки Від’ємні поздовжні сили спрямовані так щоби викликати стиск в перерізах До того у вузлі діють вертикальна й горизонтальна опорні реакції а також зовнішній зосереджений момент Складаючи для вузла рівняння рівноваги маємо
Fx 19,2 4 15,2 0,
Fy 2,536 1,6 0,836 0.M A 18 8 10 0.
Перевіримо відповідність між епюрами М і Q на ділянках де епюра М прямолінійна