9060_d71504bbdcb8f95ffb66490c84b51bf8

роена как дизъюнкция конъюнкций.

О: Дизъюнкция конъюнкций из аргументов и их отрицаний называется нормальной дизъюнктивной формой.

Т: Любая булева функция n переменных может быть представлена в виде нормальной дизъюнктивной формы n

Доказательство в [10. C. 38].

Таблице (37.1) кроме нормальной дизъюнктивной формы соответствует согласно определению эквивалентности F(p1,p2)

p1 p2. Таким образом, одна и та же булева функция может быть задана разными формулами.

О: Формулы, представляющие одну и ту же булеву функцию, называются эквивалентными, или равносильными.

Простейшие равносильности, которые используются для упрощения формул, приведены в ОК 37.2.

Для преобразования формул кроме равносильностей 1—12 необходимы следующие две теоремы.

Т.1 (о подстановке формулы вместо переменной):

Пусть P(p1, ..., pn) Q(p1, ..., pn), F — некоторая формула. Тогда при подстановке вместо pi формулы F равносильность P Q сохраняется n

Т.2 (о замене подформул): Пусть P(p1, ..., pn) Q(p1, ...,pn), ÑÐ — формула, содержащая Р, СQ — результат замены в ней Р на Q. Тогда СÐ ÑQ n

"%

Теоремы являются следствием сохранения таблиц истинности рассматриваемых формул [9. С. 14].

Примеры:

Записываем представление соответствующей таблице булевой функции в виде нормальной дизъюнктивной формы, ис-

Такого рода задачи необходимо решать при синтезе контактных схем. Они возникают также в теории распознавания образов, где по определенному набору фактов (высказываний) связываются причины и следствия. Эта теория находит применение в геологии, химии, медицине, социологии.

"%

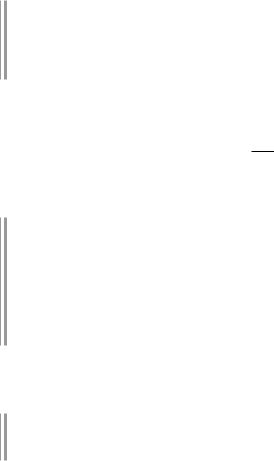
37.3.Элементы логики предикатов

Âтеории формальных систем, алгоритмических языков, а также в таких науках, как медицина, геология, социология применяются выражения, имеющие форму высказываний, но содержащие аргументы (так называемые п р е д м е т н ы е переменные).

Например, «х — простое число» — не высказывание, но обра-

щается в него при замене х конкретным значением х n N.

О: Предикатом Р(х1, õ2, ..., õn) называется функция, аргументы (предметные переменныå) êоторой принимают значения на множестве М: хi M, i 1,n, а область значений Р {0, 1}. В зависимости от числа предметных переменных предикат называется одноместным, двухместным, ..., n-местным.

Например, «х — простое число» — одноместный предикат Р(х), х N; x < y — двухместный предикат P(x,y), x R, y R; «х и у — родители z» — трехместный предикат P(x,y,z) на множестве людей.

Предикат P(x1, x2, ..., xn), xi M, i 1,n, становится высказыванием, если вместо хi подставить значения (предикатные посто-

О: Предикат P(x1, x2, ..., xn) называется тождественно-истин- ным на М, если при подсòàíовке вместо x1, x2,..., xn любых

ном случае — тождественно-ложным. Предикат наçûâàåò-

P(x1, x2, ..., xn) тождественно-истинный, называется областью истинности предиката.

Например, предикат |x| 0 тождественно-истинный на R, предикат |x| < 0 — тождественно-ложный на R.

О: Два предиката P(x) и Q(x) называются эквивалентными, если они определены на одном и том же множестве М и их множества истинности совпадают.

Аналогично определяется эквивалентность n-местных предикатов.

"%!

Предметные переменные не ÿâëяются логическими, а сам предикат P(x1, x2, ..., xn), xi M, i 1,n, является логической переменной, поэтому из предикатов можно составлять формулы логики высказываний с помощью знаков логических оперàöèé .

Например, P(x1, x2) (Q(x3, x4) R(x2, x4)) может рассматриваться как булева функция трех логических переменных P, Q, R, а также как составной четырехместный предикат от предметных переменных x1, x2, x3, x4.

Кроме логических операций вводятся операции, которые относятся только к логике предикатов, называемые кванторами.

О: Квантором общности называется знак х. Высказывание хР(х) означает: для всех х из М значение Р(х) 1.

Квантором существования называется знак х. Высказывание хР(х) означает: существует х из М, что Р(х) 1. Переход от Р(х) к хР(х) или хР(х) называется связыванием переменной х. Переменная, к которой применен квантор (говорят также, навешен квантор), называется связанной. Несвязанная переменная называется свободной.

Если Р(х) — предикат «х — четное число», то высказывание хР(х) истинно на множестве четных чисел, высказывание хР(х)

истинно на любом множестве, содержащем хотя бы одно четное число.

Если квантор навешен на n-местный предикат, то в нем коли- чество свободных переменных уменьшается, их будет n 1. Так,

xiP(x1, x2, ..., xn) Q(x1, x2, ..., xi 1, xi+1, .., xn).

Важнейшей целью логики предикатов является исследование множества истинных формул логики предикатов, для чего используются определенные формальные методы, что приводит к необходимости изучения формальных систем [10. C. 215].

37.4. Понятие о формальных системах, языках и грамматиках

Если формулы алгебры логики рассматривать не как способ представления булевых функций, а как составные высказывания, образованные из элементарных высказываний с помощью логи- ческих связок , то для этих формул строится формаль-

"%"

ная теория, называемая исчислением высказываний. Для этого выделяется подмножество формул, называемых аксиомами, и задаются правила вывода теорем. Рассмотрим в связи с этим некоторые понятия, связанные с формальными системами.

О: Алфавитом V называется конечное множество, элементами которого являются символы (буквы, цифры, знаки препинания, знаки операций, и т.д.). Последовательности n символов называются словами (цепочками) длиной n в алфавите V, причем запятые не ставятся.

Алфавит исчисления высказываний состоит из переменных

Словами являются формулы А, В, С. Между равносильными формулами ставится знак эквивалентности ~. Алфавит исчисления предикатов состоит из предметных переменных х1, õ2, ..., предметных постоянных а1, à2, ..., функциональных букв F, Q, P, знаков логических связок, кванторов и скобок ( ).

Для построения исчисления высказываний задается, кроме

Далее задаются правила вывода формул [11. С. 432]. Аксиомы исчисления предикатов — это аксиомы исчисления

высказываний плюс аксиомы:

9.õF(x) F(y)

10.F(y) xF(x).

Пусть задан алфавит V и тем самым множество V* конечных слов или цепочек в алфавите V.

О: Формальным языком L в алфавите V называется произвольное подмножество L V*.

"%#

Конструктивное описание формальных языков осуществляется с помощью формальных систем специального вида, называемых формальными грамматиками.

булевых формул с тремя переменными a,b,c порождается грамма-

ется от языка формул исчисления высказываний отсутствием импликации. Более подробно о формальных грамматиках см. [10. С. 261–295].

Литература: [10. C. 50–88, 144–295]; [9. C. 8–162].

38. ГРАФЫ Опорный конспект ¹ 38

О: Мультиграф — граф, имеющий кратные ребра.

"%$

О: Степенью вершины графа G называется число ребер, инцидентных а.

Граф изображается диаграммой или задается матрицей смежности ( ij) n-го порядка, в которой ij равно числу ребер, инцидентных a и a для неориентированного графа.

ij

38.2.Маршруты, цепи и циклы

О: Маршрут М в графе G {V, E} М {lij}, где два соседних ребра имеют общую инцидентную вершину.

Цепь — маршрут М, у которого все ребра различны. Простая цепь — маршрут М, у которого все вершины, кроме, быть может, первой и последней, различны.

Цикл — цепь, в которой начальная и конечная вершины совпадают.

О: Граф G связный, если любая пара его вершин соединяется цепью.

О: Эйлеров граф связный неориентированный мультиграф, для которого существует цикл, содержащий все ребра.

Т: Связный неориентированный мультиграф эйлеров т. и т.т., когда степени его вершин четны.

38.3. Некоторые классы графов О: Дерево — связный граф без циклов, лес — несвяз-

ный граф без циклов.

Любая цепь в таком графе — простая. Любые две вершины дерева связаны одной и только одной цепью.

О: Остовом графа G = {V,E} называется дерево H = {V,E*}, E* E.

О: Двудольный граф G ={V,E} V = V1 + V2, причем каждое ребро имеет один конец из V1, другой — из V2.

38.1. Основные понятия и способы задания графов

Одним из основных разделов дискретной математики является теория графов. Они используются при решении различных задач теории автоматического управления, а также в других науках, где возникают системы с большим числом объектов, связанных между собой разнообразными отношениями: большие молекулы, системы трубопроводов, технологические линии, сети железных

"%%

дорог, системы заводов потребителей и предприятий поставщиков и т.п.

О: Графом называется упорядоченная пара конечных множеств G {V, E}, где V {a1,a2,...,an} — множеñòâо точек, называемых вершинами графа, Е {( ai,aj)}, i,j 1,n, — множество пар элементов из V, называемых ребрами графа. Ребро (ai, aj) соединяет вершины ai è aj или инцидентно этим вершинам. Вершины ai, aj называются смежными или инцидентными ребру (a ,a ). Два ребра называются смежны-

ij

ми, если они инцидентны одной вершине. Граф с n вершинами и m ребрами называется (n,m)-графом. Граф G называется ориентированным (орграфом), если Е — множество упорядоченных пар из V, т.е. его ребра являются направленными, такие направленные ребра называют дугами.

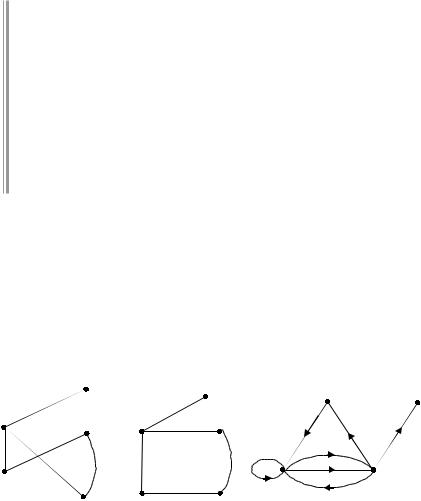
Каждому графу можно поставить в соответствие некоторую схему на плоскости, если вершины изображать точками, а ребра — линиями. Эта схема называется диаграммой графа или просто графом. Ребра на диаграмме могут быть отрезками прямых или дугами линий. Один и тот же граф можно изобразить разными диаграммами. Например, на рис. 38.1, 38.2 изображен один и тот же неориентированный граф G (V, E), где V {a, b, c, d, e}, E {(b,a), (b,e), (b,c), (d,c), (d,e)}. Такие диаграммы называются изоморфными.

На рис. 38.3 изображен ориентированный граф G = (V, E), V = {a, b, c, d}, E = {(a, b), (b, b), (b, c), (c, b), (b, c), (c, a), (c, d)}. Этот граф имеет петлю (ребро, соединяющее вершину с ней са-

"%&

мой) и кратные ребра (две вершины соединены более чем одним ребром).

О: Граф, имеющий кратные ребра, называется мультиграфом, не имеющий кратных ребер — простым графом.

О: Степенью вершины а графа G называется число ребер, инцидентных а.

Например, для графа на рис. 38.3 степень вершины а равна 2, вершины b —5. Задать граф можно также с помощью некоторой матрицы.

зывается квадратная матрица ( ij), n-го порядка, столбцам и строкам которой соответствуют вершины графа. Для неориентированного графа число ij равно числу ребер, инцидентных ai è aj. Для орграфа ij равно числу ребер с нача- лом в a и концом в a .

ij

Например, матрицы смежности графов на рис. 38.1 и 38.3 соответственно:

Матрица смежности неориентированного графа симметрична:

, и сумма чисел в любой ее строке (столбце) равна степени

ij ji

соответствующей вершины.

Обратно, по матрице смежности можно построить диаграмму графа.

Итак, граф можно задать матрицей смежности, диаграммой или списком ребер.

"%'

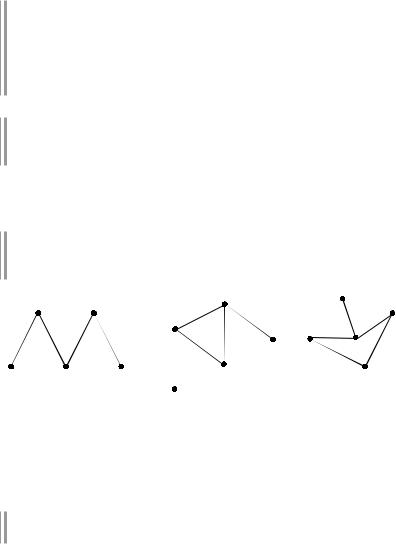
38.2. Маршруты, цепи и циклы

ребра имеют общую инцидентную вершину, а1 — начальная, аn — конечная вершины. Длиной маршрута называется число ребер маршрута.·

О: Маршрут М называется цепью, если все его ребра различ- ны, и простой цепью, если все его вершины, кроме, может быть, первой и последней, различны.

Например, для графа на рис. 38.4 имеем: abdbe — маршрут, но не цепь, abcdbe — цепь, но не простая, abe — простая цепь.

О: Цепь, в которой начальная и конечная вершины совпадают, называется циклом, если цепь простая, — простым циклом.

Например, на рис. 38.4: acbdeba — цикл, но не простой, acdeba — простой цикл.

В частности, любая петля является циклом.

О: Граф называется связным, если любая пара его вершин соединяется цепью.

Например, граф на рис. 38.4 — связный, на рис. 38.5 — несвязный.

"&