9060_d71504bbdcb8f95ffb66490c84b51bf8

Векторная запись формулы Остроградского–Гаусса:

Для гармонического ВП $u(M): Du = 0,

D = ¶2 + ¶2 + ¶2

¶¶ ¶ — оператор Лапласа x2 y2 z2

!"

28.1.Скалярное поле и его характеристики

28.1.1.Определение СП. Линии и поверхности уровня

Рассмотрим функцию u(M), где M(x,y) О D НR2 èëè M(x,y,z) Î W Í R3.

О: Mножество D точек M пространства R2 (èëè R3) вместе с

соответствующими этим точкам числами, которые опреде-

ляются функцией u(M), называется скалярным полем (СП),

а функция u(M) — функцией поля.

Åñëè D Í R2 , то СП является плоским, если W Н R3 — ïðî-

странственным.

Примерами СП являются поле распределения температуры в

данном теле, поле распределения электрического потенциала в

пространстве вокруг электрического заряда и т.п.

СП функции u(M), MОD, не зависит от времени t. Такое поле

называется стационарным. Геометрически СП изображается на

плоскости линиями уровня u(M) = u(x,y,) = c, где с — значение

u(x,y), в пространстве — поверхностями уровня u(x,y,z) = c.

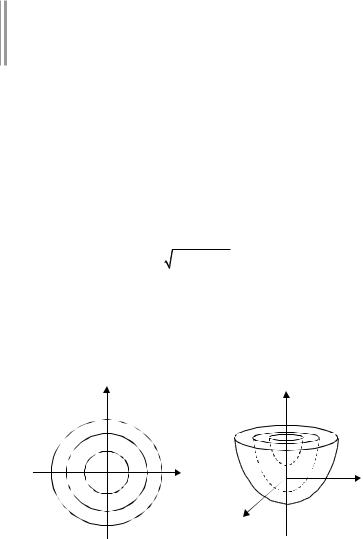
Примеры: 1) u(x, y) = x2 + y2 - 1, D: x2 + y2 ³ 1, уравнения линий уровня: x2 + y2 = 1 + ñ2, "ñ ³ 0 (ðèñ. 28.1).

2) u(x,y,z) = x2 + y2 - z, D Í R3, уравнения поверхностей уров-

íÿ: x2 + y2 = z + с, "с О R — семейство параболоидов вращения

с осью вращения OZ и вершинами, расположенными на OZ

(ðèñ. 28.2).

!"

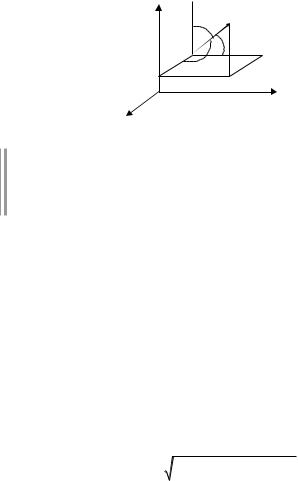
28.1.2. Производная по направлению СП

Рассмотрим пространственное СП функции u(x,y,z),

M(x,y,z) О W. Определим величину, характеризующую скорость из-

мененияr этого поля в т. M в направлении единичного вектора

l = {cos a, cos b, cos g}, расположенного на прямой L. Пусть т. M

1

(xi,yi,zi) ÎL (ðèñ. 28.3).

Z

M

1

XÐèñ. 28.3

Dr = Dx 2 + Dy 2 + Dz 2 .

Вдоль прямой L имеем Dx = r cos a, Dy = r cos b, Dz = r cos g, Dr = r, поэтому

!"!

rЗнак (-) указывает на то, что СП u(M) в направлении векто-

ðà a убывает

28.1.3. Градиент СП

Пусть функция СП u(x,y,z) дифференцируема в W.

O: Градиентом поля u(M) в т. M О W называется вектор

T: Пусть функция СП u(x,y,z) дифференцируема в W. Тогда про-

изводная по данному направлению равнаr скалярному произ-

ведению grad u на единичный векторl этого направления, т.е.

Используем определение скалярного произведения, тогда из (28.1)

!""

¶u

Таким образом, ¶l имеет наибольшее значение в т. M, если

Это значит, что grad u указывает направление наибольшего воз-

растания поля в т.M и имеет модуль, равный скорости этого воз-

растания.

Если рассматривается поверхность уровня G: u(x,y,z) = c,

M (x ,y ,z ) О G, то используя уравнение касательной к поверхно-

выясняем, что (grad u)M направлен по нормали к поверхности уровня u(x,y,z) = c. 0

Для обозначения grad u применяется векторный дифференциаль-

ный оператор, называемый оператором Гамильтона (набла-оператор):

!"#

28.2.Векторное поле и его характеристики

28.2.1.Определение ВП. Векторные линии

времени, такое поле называется стационарным.

Примерами векторных полей являются:

1) стационарное гравитационное поле силы тяжести r

2) стационарное поле скоростей v(M ) жидкости, текущей в про-

странственной области W;

3) электрическое и электромагнитное поля на плоскости;

4) векторное поле grad u скалярного поля дифференцируемой

функции u(M), M О W.

M

3

Система (28.2) является системой двух

дифференциальных уравнений для опре-

r

деления векторных линий поля v(M ).

Ðèñ. 28.5

Векторные линии характеризуют ВП геометрически и дают ин-

формацию о структуре этого поля.

!"$

это уравнения векторных линий, являющихся линиями пересече-

ния гиперболических и параболических цилиндров

28.2.2. Поток и дивергенция ВП

Рассмотрим ВП функции r( ) = {n (M), n (M), n (M)}, M Î W.

v M x y z

Пусть двусторонняя ориентированная поверхность G М W,

r( ) = {cosa(M), cosb(M), cosg(M)} — единичный вектор норма- n M

ëè â ò. M.

О: Потоком ВП r( ), M О W, через поверхность G называется v M

Окружим т. M О W замкнутой поверхностью G М W, внутри ко-

торой заключен объем V (рис. 28.6).

Рассмотрим гидродинамическую интерпретацию, т.е. будем r

считать, что v(M ), M О W, — стационарное поле скоростей несжи-

маемой жидкости. Течение жидкости может быть обусловлено су-

ществованием в W источников (точек, производящих жидкость)

и стоков (точек, поглощающих жидкость). Для замкнутой повер-

хности G величина ПG характеризует количество жидкости, про-

текающей в единицу времени с внутренней стороны G на вне-

!"%

Z

G

·Ì

O Y

W

X

Ðèñ. 28.6

Ðèñ. 28.6

шнюю (положительную) сторону, и равна суммарной мощности

источников внутри G. Тогда (28.4) является формулой для плот-

M Î W r

ности мощности источников в т. . Если div v(M ) > 0, òî â ò. r

div v(M ) < 0,

В электростатическом поле, созданном электрическими заря-

дами, распределенными в W, дивергенция является плотностью

распределения зарядов в т. M О W.

Ò: Åñëè nx(M), ny(M), nz(M) непрерывны в W вместе со

своими частными производными, то для ВП r( ) = v M

= {nx(M), ny(M), nz(M)} в W справедлива формула

q По формуле Остроградского–Гаусса (27.9) и теореме о сред-

нем для тройного интеграла поток в (28.4)

ÏG = Òòò vxdy dz + vydx dz + vz dx dy =

¶W* = G, V — объем W*, M ОW*. При G ® M имеем M* ® M,

!"&

С помощью (28.3) и (28.5) формулу Остроградского–Гаусса

можно переписать в векторной форме:

GW

LL

Используя оператор Гамильтона, формулу (28.7) можно запи-

ñàòü â âèäå

(векторное произведение символического вектора набла С на вектор r). v

!"'

r

Вектор rot v(M ) в гидродинамической интерпретации характе-

ризует интенсивность вращательного движения жидкости в т. M О W

(или завихренность) [9. С. 25].

Пользуясь введенными понятиями, формулу Стокса (27.10)

можно записать в векторной форме. Пусть G — гладкая ориенти-

рованная поверхность (G М W), натянутая на гладкую замкнутую

LG

28.2.4.Простейшие ВП

В гидродинамической интерпретации это поле без источников.

Выясним смысл названия. Возьмем замкнутую кривую L М W и про-

ведем через каждую ее точку векторные линии. Они ограничивают

!#