
9060_d71504bbdcb8f95ffb66490c84b51bf8
.pdf
Z |
r |
|
Формула (27.10) называется формулой |
n |
|
G |
||
|
||
Стокса. |
|
|
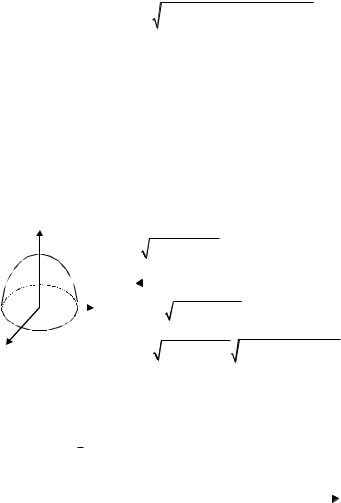
Если сторона поверхности выбрана, то |
|
|
направление обхода контура L берется по- |
|
|
ложительным, т.е. таким, что при обходе |
L |
|
O |
Y |
|
контура по выбранной стороне поверхнос- |
|
|
ти G она остается слева (рис. 27.11). Дока- |
|
|
|
|
|
|
|
X |
|
зательство см. в [6. С. 365]. |
|
|
Ðèñ. 27.11 |
||||
|
|
|
|
||||
Из формулы Стокса следует, что если |
|
|
|||||
¶Q = |
¶P , |
¶R = |
¶Q , |
¶P = |
¶R , |
(x,y,z) Î W, |
(27.11) |
¶x |
¶y |
¶y |
¶z |
¶z |
¶x |
|
|
то криволинейный интеграл по любой пространственной замкну-
той кривой L равен нулю:
Ñò P dx +Q dy + R dz = 0, L Ì W.
L
È
Как и в случае плоской кривой AB, условия (27.11) являются
необходимыми и достаточными для независимости криволиней-
ного интеграла II рода ò P dx +Q dy + R dz от пути интегрирова-
È
AB
ния. При их выполнении подынтегральное выражение — полный
дифференциал некоторой функции u(x,y,z): Pdx + Qdy + Rdz = du,
x |
y |
z |
u = ò P(x,y0 |
,z0)dx + òQ(x,y,z0)dy + ò R(x,y,z)dz + ñ, c = const. |
|
x |
y |
z |
0 |
0 |
0 |
Доказательство аналогично плоскому случаю.
Литература: [3. С. 234–264]; [6. С. 353– 365]; [10. С. 103–
129]; [11. Ñ. 233–248].


 v(M
v(M Y
Y
 Воспользуемся формулой (27.8):
Воспользуемся формулой (27.8):