9060_d71504bbdcb8f95ffb66490c84b51bf8

сходится (свойство 20), и по признаку сравнения 1 в случае

q Изопределенияпредела"e > 0 $N = N(e):n > N Ю l - e < un+1 < l + e. un

Предположим сначала, что l < 1, e выбираем настолько малым, что-

!$

бы l + e < 1. Обозначим l + e = q, 0 < q < 1, тогда n > N Ю un+1 < qun.

Таким образом, uN+1 < quN, uN+2 < quN+1 < uNq2, uN+3 < quN+2 < uNq3,...

¥

Учитывая сходимость геометрической прогрессии åunqn, ïî-

n=1

лучаем по признаку сравнения 1 и по свойству 10 сходимость ряда

¥

åun.

n=1

Предположим, что l > 1, ò.å. l - e > 1, тогда n > N Ю un+1 > un.

n=1

n = 1, 2, 3, ... значениями некоторой функции f (x), положительной, непрерывной, монотонно убывающей на [1, ¥), т.е. f (1) = u1, f (2) = u2, ..., f (n) = u(n), ... Тогда

!$

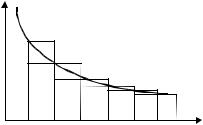
qРассмотрим криволинейную трапецию с границей ¶D: y = f(x), x = 1, x = n, y = 0 и две ступенчатые фигуры, состоящие из прямоугольников с основаниями [1, 2], [2, 3], ..., [n - 1, n]. Описанная ступенчатая фигура имеет высоты f (1), f (2), f (3), ... , f (n - 1) и пло-

ùàäü f (1) + f (2) + f (3) +...+ f (n - 1) = Sn - un, вписанная — высоты

f (2), f (3), ..., f (n) и площадь f (1) + f (2) + f (3) + ... + f (n) = Sn - u1, åñëè Sn = u1+ + u2+...+un (ðèñ. 29.1).

n

Площадь криволинейной трапеции Sêð.òð = ò f (x)dx удовле-

1

творяет неравенству

n

Sn - u1 < ò f (x)dx < Sn - un.

1¥

Пусть несобственный интеграл ò f (x)dx сходится, т.е. существует

n

Sn - u1 < ò f (x)dx < Sn - un имеем Sn < u1+J, т.е. последовательность

1

{Sn} возрастает и ограничена сверху, поэтому существует lim Sn = S

n®¥

[4. С. 48] и данный ряд сходится.

!$!

ная последовательность. Из неравенства Sn - u1 < ò f (x)dx < Sn - un

имеем Sn > ò f (x)dx + un, т.е. последовательность {Sn } возрастает и

1

неограничена, следовательно, ряд расходится x

Пример: Исследовать на сходимость обобщенный гармонический

¥

ðÿä å 1 , p > 0.

n =1 np

29.5. Знакочередующиеся числовые ряды. Признак Лейбница

О: Знакочередующимся числовым рядом называется ряд

¥

å(-1)n-1un, un > 0.

то этот ряд сходится, причем его сумма S > 0 и S £ u1 n

!$"

q Рассмотрим частичную сумму S2m, члены которой сгруппи-

ðóåì ïî äâà:

S2m = (u1 - u2)+(u3 - u4)+...+(u2m - 1 - u2m).

В силу условия 1) разности в скобках положительны, поэтому последовательность {S2m} возрастающая и S2m > 0. Перегруппируем

члены S2m: S2m = u1 - (u2 - u3) - (u4 - u5) - ... - (u2m - 2 - u2m - 1) - u2m, отсюда S2m < u1. Возрастающая и ограниченная последовательность

имеет предел lim S2m = S £ u1.

m®¥

Для последовательности нечетных сумм {S2m+1} в силу условия 2)

29.6. Знакопеременные ряды. Абсолютная и условная сходимости

¥

О: Знакопеременным числовым рядом называется ряд åun,

n=1

который содержит как положительные, так и отрицательные

члены.

Знакочередующийся ч.р. является частным случаем знакоперемен-

íîãî ÷.ð.

Т. (признак абсолютной сходимости): Если для знакопеременно-

¥

личин его членов, то ряд åun, сходится n

n=1

q Обозначим Sn = u1 + u2 + ... + un, Sn¢ — сумма положительных

членов в Sn, Sn¢¢ — сумма абсолютных величин отрицательных членов в Sn, sn = |u1| + |u2| + ...+ |un|. Тогда Sn = Sn¢ - Sn¢¢, sn = Sn¢+ Sn¢¢,

!$#

ных величин сходится, поэтому данный знакопеременный ряд сходится

по признаку абсолютной сходимости

Признак абсолютной сходимости является достаточным, но не

¥ - n-1

ån — условно сходящийся ряд.1=

n 1

!$$

Деление знакопеременных ч.р. на абсолютно и условно сходящие-

ся существенно. На абсолютно сходящиеся ч.р. переносятся все основные свойства конечных сумм. Особо важное свойство состоит в том, что сумма абсолютно сходящегося ч.р. не меняется при любой

перестановке бесконечного числа его членов. В условно сходящем-

ся ч.р. в результате такой перестановки можно получить расходящий-

ñÿ ðÿä [1à. Ñ. 315].

Литература: [6. С. 379–391]; [10. С. 129–150]; [11. С. 254–272].

30. СТЕПЕННЫЕ РЯДЫ

Опорный конспект ¹ 30

30.1. Понятие функционального и степенного рядов. Теорема Абеля

|x| > |x1|.

!$%

30.2. Радиус и интервал сходимости с.р.

солютной сходимости ( -R, R), для ряда (1) интервал абсолютной сходимости (х0 - R, õ0 + R).

30.3. Дифференцирование и интегрирование с.р.

Дифференцирование и интегрирование с.р. проводится по- членно в интервале абсолютной сходимости, интервал сохраняется.

30.4. Ряды Тейлора и Маклорена

Î: Rn(x) = f(x) - Sn(x) — остаточный член.

член в форме Лагранжа (x между х0 è õ)

!$&

30.6. Разложение в ряд Маклорена основных

30.7. Применение рядов к приближенным вычислениям

30.7.1. Вычисление значений функции

лютной сходимости.

x1 Î (x0 - R, x0 + R) Þ f(x1) » Sn(x1),

абсолютная погрешность D = |Rn(x1)|.

30.7.2. Вычисление интегралов с помощью рядов

xx

ò f (x)dx » òSn (x)dx.

aa

30.7.3. Решение дифференциальных уравнений с помощью рядов

Задача Коши:

y ¢¢ = f(x,y,y ¢), y|x0 = y0, y ¢|x0 = y ¢0.

!$'

Решение y(x) ищем в виде

y(x0) = y0, y ¢(x0) = y0¢, y ¢¢(x0) = f(x0,y0,y0¢),

30.1. Понятие функционального и степенного рядов. Теорема Абеля

О: Функциональным рядом (ф.р.) называется ряд u1(x) + u2(x) + + ... + un(x) + ..., члены которого являются функциями от х.

При фиксированном х = х0 функциональный ряд становится чис-

ловым. Областью сходимости ф.р. называется множество Х всех зна-

чений х, для которых он сходится.

¥

В области сходимости Х ф.р. åun (x) его сумма S(х) является

n=1

функцией от х.

Пример: e-x + e-2x +...+ e-nx +... - ф.р. Найти область сходимости.

Так как члены его положительны, то для нахождения области сходимости можно воспользоваться признаком Даламбера (п. 29.4.2):

при х > 0 ряд сходится

Важным частным случаем ф.р. является степенной ряд.

!%