∆V (R

, H

0

)

≈ 200π (− 0,1)

+ 100 π 0,3 = −20π +10π ≈ −31,4 (см2 ).

0

3

Получили, что объем конуса уменьшился примерно на 31,4 см2.

§9. Полные дифференциалы высших порядков

Рассмотрим функцию z = f (x, y),

непрерывную,

дифференци-

x

y

D.

Дифференциалx y

руемую в некоторой области

1-го порядка такой

функции имеет вид (13)

d z = z′x d x + z′y

d y .

А2

Дифференциал второго порядка – это дифференциалИот диффе-

ренциала первого порядка, т.е. d 2 z = d ( d z). Вычислим второй диф-

ференциал:

б

2

= d (z

′

′

d y)= (z

′

′

′

d z

d x + z

d x + z

d y)x d x +

и

+ (z′x d x + z′y d y)′y

d y = z′′xx d x2 + z′y′x d y d x +

′′

′′

′′

′′

d x d y

′′

+ zxy

d x d y + zy y d y = z xx d x

+ 2 zxy

+ zy y d y .

С

Итак,

второй д фференциал (полный дифференциал 2-го поряд-

ка) функц

двух переменных имеет вид

2

′′

2

′′

′′

d

z = z xx d x

+

2 zxy

d x d y + zy y d y .

(17)

Аналогично

находим

дифференциал 3-го порядка. Т.к.

d 3 z = d (d 2 z), то

d

3

z = d

′′

2

′′

′′

(z xx d x

+ 2 zxy d x d y + zy y d y).

3

′′′

d x

3

′′′

2

′′′

2

′′′

3

d x d y

d y .

(18)

d z = z xx x

+ 5 zx x y d x

d y + 3zx y y

+ zy y y

Аналогично можно найти полный дифференциал порядка n:

d n z = d (d n−1z).

(19)

Замечание. Коэффициенты n-го дифференциала функции двух

переменных

такие

же, как

в

формуле

сокращенного

умножения

( x + y)n . Для упрощения используют условное обозначение n-го диф-

ференциала для функции z = f (x, y):

И

d n z

∂

∂

n

=

d x

+

d y

z .

∂ x

∂ y

Формула Тейлора функции нескольких переменных

Д

(x) в точке

Формула Тейлора функции одной переменной

y

=

f

x = x0

вид

f

′

)

f

′′

(x

)

2

f

(n)

(x

)

n

(x

0

0

А0

(x − x0 ) + ...

y (x) = f (x0 )+

(x − x0 )+

(x

− x0 ) + ... +

1!

2!

n!

Преобразуем формулу. Т.

к.

( x − x0 )n

= ∆ xn

= d xn , далее ис-

б

пользуем формулы полного дифференциала функции y = f (x) одной

переменной

в

точке

M0 = M0 (x0 ):

f ′(x0 )d x = d f (M0 );

f ′′(x0 )d x2 = d 2

f

(M

0 ); … ;

f (n)

(x0 )d xn

= d n f (M0 ). Теперь запишем

имеет

формулу Тейлора

в виде

f (x) = f (M0 )+

d f (M0 )

+

d 2 f (M0 )

+ ... +

d n

f (M0 )

+ .... .

(20)

С

1!

2!

n!

менных изменяем

вид

полных

дифференциалов

d y (x0 ),

d 2 y (x0 ),

d n y (x0 ). Например, для функции двух переменных z = f (x, y)

исполь-

зуем полные дифференциалы в виде выражений (13), (17),

(18), (19).

M0 – точка двух переменных).

И

Пример.

Найти

разложение

по

формуле Тейлора функции

Д

z = 2x2 + 3y2 − 4 y + 6 в точке M0 (−1;1).

M0 (−1;1):

Решение.

Вычислим

значение функции в

точке

z (−1,1) = 7. Далее найдем дифференциалы данной функции.

ля это-

го вычислим частные производные этой функции в точке M

0 (−1;1).

А

z′x = (2x

2

+ 3y

2

−

4 y

′

= 4x ;

z′x (−1,1) = 4(−1) = −4 ;

+ 6)x

z′y = (2x2 +

3y2 − 4 y + 6)′y

= 6y ;

z′x (−1,1) = 6 1 = 6.

б

d z(−1,1) = −4 d x + 6 d y.

Получаем вид 1-го дифференциала:

Теперь вычисляем частные производные второго порядка:

и

z′′xx

=

(4x)′x

= 4;

z′y′y

= (6 y)′y = 6;

С

z′′xy = (4x)′y = 0;

z′y′x = (6 y)′x = 0 .

d 2 z(−1,1) = 4 d x2 + 6 d y2.

Получаем в д 2-го д фференциала:

Частные про зводные 3-го и более высоких порядков все равны

нулю. Поэтому d 3 z(−1,1) = 0 , …

d (n) z(−1,1) = 0.

Теперь выписываем формулу Тейлора в виде (20)

f (x) = 7 + − 4 d x + 6 d y +

4 d x2 + 6 d y2 .

1!

2!

§10. Производная функции по направлению вектора

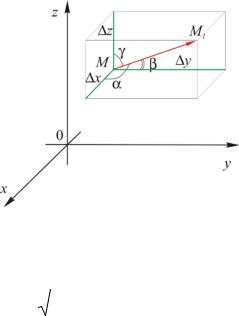
Рассмотрим функцию трех переменных

u = u (x, y , z ),

опреде-

ленную

и дифференцируемую

в некоторой трехмерной

области

V R3 .

Пусть в области V

заданы

точки М (x, y , z ) и

Д

А

И

→

Рис. 12

Тогда вектор

M М1

{∆ x, ∆ y,

∆ z}

– это

вектор

перемещения.

б

→

∆ x2 + ∆ y2 + ∆ z2 = ρ . При переходе от точ-

Длина вектора

M М1 =

М1

→

ки М

к точке

, т.е.

по вектору M М1

,

функция u = u (x, y , z )

приращение

).

получает

∆ u = u (M1 ) − u (M

Так как д фференц ал функции примерно равен приращению

функц

d u ≈ ∆ u ,

то, спользуя формулу полного дифференциала,

меем равенство

С

∆ u ≈ u′x ∆ x + u′y ∆ y + u′z ∆ z .

Рассмотр м отношен е

∆ u

. Физический смысл этого отноше-

ρ

ния – это средняя скорость изменения функции u = u (x, y , z ) при пе-

реходе от точки М к точке М1

. Переходим к пределу при условии

ρ → 0 . Получаем

lim

∆ u

= lim

∆ x

+ u′y

∆ y

+ u′z

∆ z

(21)

ρ

u′x

ρ

ρ

ρ

.

ρ→0

ρ→0

Отношения

∆ x

= cosα ;

∆ y

= cos β ;

∆ z

= cosγ

– это коорди-

ρ

ρ

ρ

→

наты орта вектора M М1

, которые равны направляющим косинусам

→

вектора перемещения M М1 . Поэтому равенство (21) можно перепи-

сать в виде

И

lim

∆ u

= u′x cosα + u′y cos β + u′z cosγ .

(22)

ρ→0

ρ

Д

Предел lim

∆ u

называется производной функции u = u (x, y , z )

ρ→0

ρ

∂ u

по направлению вектора

→

M М1

, обозначается

и вычисляется

→

по формуле

А

∂ M M1

∂ u

б′

(23)

→

= u′x

cosα + u′y cos β + u′z cosγ .

∂ M M1

Примеры.

осями

u = x2 − 3y z + 5

в точке

1.

Вычислить производную функции

M0 (1; 2; −1) в направлен

вектора, о разующего одинаковые острые

углы с

коорд нат.

Решен е. Для решен я задачи используем формулу (23). Нахо-

С

д м частные про зводные функции в точке M0 (1; 2; −1):

u′x = (x2 − 3y z + 5)x = 2 x ;

u′x (M0 ) = 2 1 = 2;

u′y = (x2 − 3y z + 5)′x = −3 z ;

u′y (M0 ) = −3 (−1) = 3;

u′z = (x2 − 3y z + 5)′x = −3 y ;

u′z (M0 ) = −3 2 = −6 .

cos 2α + cos 2β + cos2 γ = 1.

(24)

По условию, все углы равны, поэтому равенство (24) имеет вид

3cos 2α = 1,

Находим, что

Д

cos α

= cos

β = cosγ

=

1

.

3

А

По условию углы, которые образует вектор с осями координат,

острые, поэтому направляющие косинусы являются Иположительными.

Используем формулу (23), вычисляем производную функции по на-

правлению вектора

→

(1; 2; −1):

a в точке M0

б

∂ u

(M0 ) =

2

1

+ 3

1

− 6

1

= −

3

.

→

3

3

3

3

∂ a

Замечан е. Про зводная функции u = x2 − 3y z + 5 по направле-

→

(1; 2; −1) отрицательна. Это означает, что в

н ю вектора a

в точке M0

данной точке в указанном направлении функция убывает. Угол на-

С

→

клона касательной в направлении вектора a находим из свойства

и

∂ u

(M0 ) = tgϕкас = −

3

,

→

3

∂ a

т.е. ϕ

кас

= 30o – угол убывания.

2.

Вычислить производную функции

u = x2 − 3y z + 5 в точке

M0 (−1;

−1; 0) в направлении вектора M0→М1

, где координаты точки

Решение. Для решения задачи используем формулу (23). Вычис-

ляем

частные производные функции

И

u = x2 − 3y z

+ 5

в

точке

M0 (−1; −1; 0):

u′x = (x2 − 3y z + 5)′x = 2 x ;

u′x

(M

0 ) = 2 (−1) = −2 ;

u′y = (x2 − 3y z + 5)′x = −3 z ;

Д

u′y (M0 ) = −3 0 = 0;

u′z = (x2 − 3y z +

5)′x

= −3 y

;

u′z

(M

0 )

= −3 (−1) = 3.

А

Вычислим направляющие косинусы вектора.

По условию задачи,

вектор

перемещения –

это

вектор

M →М

={2, 3, −1}. Находим орт вектора M

→

0

1

0

1

вектора:

M0→М1

=

=

.

координатыТ.к.

22 + 32 + (−1)2

14

орта равны направляющим косинусам, то

Коорд наты орта равны

С

→

→

o

M0M1

2

3

−1

бM М =

=

;

;

.

0

1

→

14

14

14

M0M1

cos α =

2

;

3

;

−1

.

cos β

=

cosγ =

14

14

14