мат. модел в почв

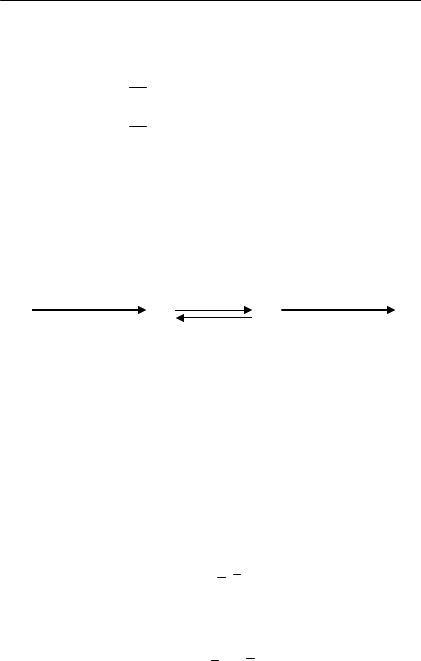
Часть I. Построение математических моделей

Динамическая модель для этой системы имеет следующий вид:

da =k1 (A −a) +k−2b −k+2a = f1 (a,b) dt

db =k+2a −k−2b −k3 (b −B) = f2 (a,b) (3.7) dt

Где «а» и «b» – переменные состояния, характеризующие концентрации этих веществ в системе; А, B – постоянные концен трации этих веществ во внешней среде; k1, k+2, k 2, k3 – константы скоростей процессов.

Рис. I.3.3. Открытая система – простейшая модель обменных процессов

(по Рубин, 1998).

Так как по определению в стационарном состоянии скорость изменения переменных а и b равна 0, следовательно, производ

найдем стационарные значения a , b . Они не зависят от началь ных условий, то есть от значений переменных a и b в момент вре мени t=0. Это означает, что при каком бы начальном состоянии система не находилась, в ней со временем установится стацио нарный режим, при котором a =a , b =b .

61

Математическое моделирование в почвоведении

Хотя начальные условия не влияют на стационарные значе ния, они определяют характер кривых, описывающих изменения переменных состояния при переходе от начального состояния при t=0 к стационарному при t → ∞.

На примере этой модели А.Б. Рубин (1998) показал, что даже такая, до предела упрощенная, модель отражает основные черты совокупности метаболических реакций клетки как открытой сис темы. Она может быть использована для описания обменных процессов и в других открытых системах, например, в почве, что является еще одной демонстрацией универсальности математи ческих моделей. Если модели, описывающие различные объекты, основаны на одинаковых предположениях, то для их описания могут быть использованы одни и те же математические выраже ния. Как отмечал великий французский математик Анри Пуанка ре: «Математика – это искусство давать разным вещам одно на именование».

Динамические математические модели, представляющие со бой системы обыкновенных дифференциальных уравнений вида (3.2), называются точечными. При их построении для упрощения модели пренебрегают пространственной неоднородностью изу чаемых систем. Они описывают изменения во времени только усредненных по пространству переменных состояния системы. Почвы и экосистемы характеризуются высокой пространственной неоднородностью. Чтобы описать изменения переменных со стояния не только во времени, но и в пространстве, используют пространственно распределенные модели, которые отражают не только процессы трансформации вещества, но и его миграции в системе. Они представляют собой системы уравнений в частных производных и описывают скорость изменения концентрации вещества в элементарном объеме системы как за счет его появ ления и исчезновения в результате процессов трансформации, описанных системой (3.2), так и в силу процессов переноса веще ства через границы элементарного объема. Например, когда од

62

Часть I. Построение математических моделей

новременно с реакциями превращения вещества в элементарном объеме происходит диффузия, система уравнений имеет вид:

где Dxi – коэффициент диффузии вещества xi , r – пространствен

ная координата.

Пространственно распределенные динамические модели представляют особенный интерес для почвоведов, так как позво ляют исследовать основные механизмы формирования почвенно го профиля.

В случае сложных динамических моделей с большим числом переменных состояния, отражающих нелинейные взаимодейст вия в почвах и экосистемах, возникают серьезные математиче ские трудности в поиске аналитических решений, если их вообще можно получить. В то же время, методы качественной теории дифференциальных уравнений позволяют определить важные динамические свойства системы, не прибегая к поиску решения системы уравнений. Великий французский математик Анри Пуан каре (1854 1912) первым понял, что можно, не интегрируя диф ференциальных уравнений, представить основные качественные особенности поведения их решений. Он и выдающийся русский математик Александр Михайлович Ляпунов (1857 1918) являются основоположниками качественной теории дифференциальных уравнений, которая получила бурное развитие в XX веке. Качест венное исследование системы дифференциальных уравнений эффективно тогда, когда нужно предсказать характер динамиче ского поведения системы и нет необходимости в поиске точного решения уравнений, поскольку начальные условия, значения внешних переменных и параметров системы сильно варьируют и не могут быть точно заданы. Именно с такой ситуацией обычно приходится сталкиваться при решении проблем почвоведения и экологии.

63

Математическое моделирование в почвоведении

К вопросу о… Основоположники качественной теории

дифференциальных уравнений

Качественная теория дифференциальных уравнений явля ется одним из ведущих разделов современной математики. Она позволяет изучать особенности решений дифференциальных уравнений по виду самих уравнений, не прибегая к их интегриро ванию. Основы этой теории были заложены в конце 80 х годов XIX столетия в работах Анри Пуанкаре (1854 1912) и Александ ра Михайловича Ляпунова (1857 1918).

Жюль Анри Пуанкаре (1854 1912) – гениальный французский ученый, снискавший всемирную славу. Он по праву занимает первое место среди математиков конца XIX — начала XX века. Его и немецкого математика Давида Гильберта называют «по следними универсалами», так как они замыкают ряд великих математиков, внесших выдающийся вклад в развитие многих различных областей математики. В соответствии с общей тенденцией развития науки, математика с конца XIX века бы стро развивается. Группа математиков под коллективным псевдонимом Никола Бурбаки в статье «Архитектура мате матики» пишет: «Ни один математик не в состоянии просле дить это развитие во всех подробностях, даже если он посвя тит этому всю свою деятельность. Многие из математиков устраиваются в каком либо закоулке математической науки, откуда они и не стремятся выйти, и не только почти полно стью игнорируют все то, что не касается предмета их иссле дований, но не в силах даже понять язык и терминологию своих собратьев, специальность которых далека от них. Нет такого математика, даже среди обладающих самой обширной эруди цией, который бы не чувствовал себя чужеземцем в некоторых областях огромного математического мира. Что же касается тех, кто подобно Пуанкаре или Гильберту оставляет печать своего гения почти во всех его областях, то они составляют даже среди наиболее великих редчайшее исключение».

64

Часть I. Построение математических моделей

Творческая активность Пуанкаре поражает и восхищает. Он создал новую область математики — топологию. Первым понял, что можно, не решая дифференциальных уравнений, представить все основные качественные особенности поведе ния их решений по свойствам их правых частей. Его первой ра ботой по качественной теории дифференциальных уравнений являются четыре мемуара с общим названием «О кривых, опре деляемых дифференциальными уравнениями». Богатство вы двинутых им идей позволяет сказать, что Пуанкаре является основателем не только качественной теории дифференциаль ных уравнений, но и теории динамических систем, так как ее возникновение явилось естественным развитием идей Пуанка ре. Он оставил первоклассные труды во многих областях ма тематики и физики. Научное наследие Пуанкаре огромно, оно составляет более чем 500 статей и книг. Особое место среди них занимают работы по общим вопросам науки, которые он объединил в три отдельные книги. Первая книга вышла в 1902 году под названием «Наука и гипотеза» и имела громкий успех. Вслед за первым изданием на родине автора, ее стали перево дить на другие языки. В России были изданы два независимых перевода этой книги. Вторая книга – «Ценность науки» – опуб ликована в 1905 году, а третья книга «Наука и метод» издана тремя годами позже, в 1908 году. Статьи и доклады последних лет жизни Пуанкаре вошли в четвертую книгу «Последние мыс ли», которая появилась в 1913 году уже после его смерти. Упо мянутые книги значительно повлияли на интеллектуальную атмосферу своего времени и продолжают оставаться инте ресными в настоящее время. В 1990 году издательство «Наука» выпустило сборник этих работ. В предисловии к нему академик Л.С. Понтрягин писал: «Одно из самых ярких и глубоких впечат лений моих юных лет связано с работами великого французско го ученого Анри Пуанкаре, посвященными научному творчеству

65

Математическое моделирование в почвоведении

и развитию науки. С годами это впечатление не потускнело. Я уверен, что для формирования научной молодежи, творчески работающей в области математики, физики, механики и, разумеется, философии, эти работы имеют непреходящее зна чение. Да и для всякого, кого волнуют философско методологические проблемы развития науки, играющей такую важную роль в современном обществе, они полны живейшего интереса».

Александр Михайлович Ляпунов (1857 1918) – выдающийся русский математик, представитель Петербургской матема тической школы, созданной П.Л. Чебышевым.

Его работы явились основополагающими для развития теории устойчивости и принесли ему всемирную известность.

В 1876 году А.М. Ляпунов поступил на естественное отде ление физико математического факультета Санкт Петербургского университета, но вскоре перешел на матема тическое отделение, поняв, что математика представляют для него больший интерес. В то время Петербургская матема тическая школа, основанная П.Л. Чебышевым, всемирно извест ным своими блестящими работами по теории чисел, теории вероятностей и анализу, была в самом расцвете. Лекции Чебы шева, а впоследствии его советы стали определяющими в вы боре тематики исследований Ляпунова, а обстановка на мате матическом отделении способствовала развитию исключи тельных способностей молодого ученого. Еще студентом Алек сандр Михайлович давал уроки известному биологу Ивану Ми хайловичу Сеченову по тем разделам математики, которые считал особенно важными для физиолога. В 1885 году А.М. Ляпунов блестяще защитил диссертацию, получил сте пень магистра прикладной математики и предложение занять кафедру механики в Харьковском университете. Одним из его

66

Часть I. Построение математических моделей

учеников в этом университете был В.А. Стеклов, ставший впо следствии организатором и первым директором математиче ского института РАН, который сейчас носит его имя. По вос поминаниям В.А. Стеклова, студенты, узнав, что из Петербур га прибыл новый профессор механики, решили, что это новона значенный посредственный чиновник, и были настроены к нему недружелюбно. Однако на первой же лекции случилось неожи данное. Владимир Андреевич Стеклов писал: «...в аудиторию вместе с уважаемым всеми студентами старым деканом про фессором Леваковским вошел красавец мужчина, почти ровес ник некоторым из наших товарищей, и, по уходе декана, начал дрожащим от волнения голосом читать вместо курса динами ки систем курс динамики точки, который мы уже прослушали у профессора Деларю. Шел уже 4 й год моего студенчества; в Мо скве в течение года я слушал таких лекторов, как Давыдов, Цингер, Столетов, Орлов; два года был студентом Харьковско го университета; курс механики мне уже был знаком. Но с само го начала лекции я услышал то, чего раньше не слышал и не встречал ни в одном из известных мне пособий. И все недруже любие курса разлетелось прахом; силою своего таланта, обая нию которого в большинстве случаев неосознанно поддается молодежь, Александр Михайлович, сам не зная того, покорил в один час предвзято настроенную аудиторию. С этого же дня Александр Михайлович занял особое место в глазах студентов, к нему стали относиться с исключительно почтительным уважением. Большинство, которым не были чужими интересы науки, стало напрягать все силы, чтобы хоть немного прибли зиться к той высоте, на которую влек Александр Михайлович своих слушателей. Появился особый стыд перед ним за свое не знание, большинство не решались даже начать говорить с ним только из боязни показать перед ним свое незнание».

67

Математическое моделирование в почвоведении

Однако, качественное исследование динамических моделей дает хорошие результаты при исследовании моделей, представ ленных небольшим числом дифференциальных уравнений. По этому прежде чем приступить к качественному исследованию модели необходимо сократить число уравнений в исходной мо дели, оставив только те, которые отражают наиболее важные ди намические свойства системы. Проводить редукцию количества уравнений модели нужно очень осторожно, так как есть риск по терять важные характеристики моделируемой системы и не толь ко обеднить модель, но и сделать ее вообще неадекватной. По мочь получить модель системы, содержащую наименьшее число переменных состояния и параметров, и в то же время правильно отражающую ее основные свойства, представляющие интерес в соответствии с поставленными задачами, может учет временной иерархии изучаемых процессов.

Процесс почвообразования представляет собой иерархиче ский процесс, включающий в себя множество процессов с разны ми характерными временами, причем иерархия этих времен та кова, что они различаются на много порядков.

Принимая во внимание характерные времена изучаемых процессов, можно разделить переменные состояния исходной модели на «быстрые», «средние» и «медленные». В ответ на внешнее воздействие (возмущение) все переменные системы начнут изменяться, но с очень разными скоростями. «Медлен ные» переменные будут очень долго изменяться в ходе переход ных процессов. И на интересующем исследователя временном интервале эти изменения могут быть очень малыми, которые можно не учитывать и заменить «медленные» переменные по стоянными параметрами. «Быстрые» переменные, достигнув ста ционарного состояния, будут пребывать около своих стационар ных значений. Поэтому для «быстрых» переменных вместо диф ференциальных уравнений, описывающих их поведение во вре мени, можно записать простые алгебраические уравнения, опре деляющие их стационарные значения. Таким путем можно сокра тить число уравнений в исходной модели, в которой в результате

68

Часть I. Построение математических моделей

останутся только дифференциальные уравнения, описывающие динамику «средних» переменных.

Предположим Предположим, что исходная модель описыва ет динамику трех переменных с различными характерными вре менами:

dx =P(x,y,z) dt

dy =Q(x,y,z) dt

dz =F(x,y,z) dt

Причем x − «быстрые», y − «средние», а z − «медленные» пе ременные: Tx <<Ty <<Tz .

Пусть мы наблюдаем за «средней» переменной y. Тогда за время Ty «медленная» переменная z практически не будет изме няться и ее можно считать постоянным параметром, который обозначим z*. В этом случае исходную модель можно предста вить системой двух дифференциальных уравнений:

dx =P(x,y,z*) dt

dy =Q(x,y,z*) dt

Рассмотрим теперь уравнение для х. Эта «быстрая» перемен ная за время Ty успеет достичь стационарного значения. Поэтому для нее дифференциальное уравнение можно заменить следую щим алгебраическим:

P(x,y, z*) =0 → x = x(y, z*)

Таким образом, благодаря учету иерархии времен модель, представленную системой трех дифференциальных уравнений, удалось свести к одному дифференциальному уравнению:

dy =Q(x(y, z*),y,z*) . dt

Такой метод редукции системы широко применяется в химии и биохимии для описания каталитических и ферментативных про

69

Математическое моделирование в почвоведении

цессов, где он называется методом квазистационарных концен траций (КСК). Математически строгое обоснование применения метода квазистационарных концентраций (редукции системы в соответствии с иерархией времен) и формулировка условий его применимости дано А.Н. Тихоновым (1952).

Более подробно с удачно подобранными иллюстративными примерами проблема учета временной иерархии процессов при построении моделей биологических систем обсуждается в учеб нике Г.Ю. Резниченко «Лекции по математическим моделям в биологии» (2002).

При изучении общих динамических характеристик системы и

еемодели ищут ответы на следующие вопросы:

•Имеет ли система стационарные состояния?

•Сколько их?

•Какова их устойчивость?

•Как они зависят от параметров системы?

•Возможны ли переходы между ними?

•Как ведет себя система вблизи стационарных состоя ний?

Познакомимся с методами качественной теории дифферен циальных уравнений на примере простейших моделей.

В первую очередь нас будут интересовать два вопроса:

4.Как найти стационарные состояния?

5.Как определить их устойчивость?

Рассмотрим модель с одной переменной состояния, динами

ку которой описывает одно дифференциальное уравнение перво го порядка:

Пусть f (x) – аналитическая функция.

70