мат. модел в почв

Часть II. Применение математических моделей в почвоведении

Существует два основных метода определения педотранс ферных функций.

1 й способ – точечный. Этот метод основан на том, что некая точка на ОГХ соответствует определенному давлению конкретной влажности. Например, надо найти влажность θi при i том давле нии влаги. Имея достаточный набор экспериментальных данных, который обязательно включает гранулометрический состав (на пример, в виде содержания физического песка ωпесок , пыли ωпыль , и ила ωил ), содержание органического вещества ωС , плотность почвы ρb , можно с помощью методов множественной регрессии найти эмпирические регрессионные коэффициенты a, b, c, d, e, f. Затем для конкретного образца с помощью полученной регресси онной зависимости можно найти, влажность для данного i го дав ления влаги:

θi =ai +bi ωпесок +сi ωпыль +di ωил +ei ωС + fiρb ,

где i относится к одной из равновесных точек pF θ на ОГХ, а ω – доля соответствующей фракции в гранулометрическом составе почвы, ωС – содержание органического вещества, ρb – плотность почвы, ai, bi, ci, ei и fi –коэффициенты регрессионного уравнения.

Например, (цит. по Глобус, 1987, стр.218), для некоторых пылева тых тяжелых суглинков в случае влажности, соответствующей давлению –100 см водного столба, уравнение выглядит следую щим образом:

θi =0.4118 −0.0930 ωпесок +0.023 ωил +0.0317ωС

Регрессионные коэффициенты для плотности почвы и пыли ока зались незначимыми, поэтому эти предикторы не указаны в дан ном уравнении.

Аналогичным способом можно найти влажность и для друго го давления влаги. Таким образом нужно получить достаточное количество парных точек pF θ на ОГХ, а затем провести аппрокси мацию и получить необходимые параметры α, n , θr и θs.

221

Математическое моделирование в почвоведении

2 й способ – параметрический. В этом способе методами множественно регрессии или какими либо другими определяют зависимости параметров ОГХ (α, n, θr и θs) от фундаментальных физических свойств. Этот метод быстрее и удобней, но менее то чен.

Таким образом, для того, чтобы получить и использовать пе дотрансферные функции, необходимо:

1.Иметь большую базу данных по ОГХ и базовым свойствам различных почв. Последние работы показали, что педотранс ферные функции лучше создавать для конкретного региона на своей региональной базе. Это позволяет значительно по высить их точность.

2.Выбрать способ получения педотрансферных функций. Это могут быть множественная регрессия, статистические мето ды, использующие нейронные алгоритмы, которые дают, ви димо, более точные результаты, чем простые регрессии, и многие другие.

3.Надо иметь в виду, что современные модели переноса ве ществ снабжены ориентированными базами данных и «заши тыми» внутри модели педотрансферными функциями. По этому, когда в меню модели, отражающем почвенный блок, просят ввести данные по гранулометрическому составу, плот ности почв и т.д., это означает, что используются ранее полу ченные и «зашитые» педотрансферные функции. Но необхо димо обязательно уточнить, для каких почв получены эти пе дотрансферные функции, какая использовалась база данных, какой математический способ восстановления применяется. Эти особенности получения педотрансферных функций, «за шитые» в модели, может иногда привести к серьезным ошибкам в ваших расчетах.

Только соблюдая эти правила, можно относиться к пе дотрансферным функциям, как к «волшебной палочке выручалочке»: «Педотрансферные функции превращают данные, которые у нас есть, в данные, которые нам нужны!»

222

Часть II. Применение математических моделей в почвоведении

К вопросу о…

Розеттский камень, гений Шампольона и база данных «Розетта»

Это случилось в конце XVIII века во времена походов Наполе она в Египет. Одним из руководителей его египетской эмиссии был назначен Жан Батист Фурье, великий математик и физик. Одно из уравнений теплофизики носит его имя. Фурье как то заметил одиннадцатилетнего ученика, которого товарищи прозвали «египтянином» за его знания разных языков. Так слу чилось, что в августе 1799 года французские солдаты укрепля ли форт недалеко от арабского селения Розетта в дельте Ни ла. Один солдат выкопал из земли большую плиту черного ба зальта, всю покрытую надписями. Надпись оказалась двуязыч ной: симметричные тексты на древнеегипетском (иероглифы) и на древнегреческом языках. Так весь мир впервые получил еги петский текст с его точным переводом на греческий язык. Поя вилась возможность расшифровать тайну иероглифов. Каза лось, это просто, однако никто из египтологов не смог этого сделать. За дело принялся тот самый молодой человек по про звищу «египтянин», Жан Франсуа Шампольон. Именно он после многих лет труда сумел найти ключ к разгадке. Его гениальная идея заключалась в том, что он предположил, что египетское письмо состоит не из рисунков иероглифов, а из звуковых эле ментов. Вот тогда, сравнивая отдельные египетские знаки с соответствующими греческими, он воссоздал древний египет ский язык. Так, благодаря Розеттскому камню и гению Шам польона, сейчас не составляет труда переводить с одного язы ка на другой. В США, в середине XX го века была создана база гидрофизических данных, позволяющая с помощью педотранс ферных функций по традиционным почвенным свойствам вос станавливать гидрофизические функции почвы, т.е. ОГХ и функцию влагопроводности, как с помощью Розеттского камня удалось воссоздать египетский язык. Эту базу данных её авто ры назвали «Розеттой».

223

Математическое моделирование в почвоведении

2.3. Модели с учетом преимущественных потоков влаги (модели «двойной пористости»)

Хорошо известно, что при движении влаги в почве, особенно при ливневых осадках, в почве наблюдается движение влаги по макропорам и трещинам. Именно по этим почвенным образова ниям вода и растворенные вещества движутся довольно быстро (на порядки быстрее, чем в почвенной матрице!). Причем движе ние происходит строго по макроканалам различной природы со столь высокой скоростью, что вещества не успевают сорбировать ся и проникают довольно глубоко и практически без изменений. Считается, что в 14 почвах из 15 обследованных мы имеем дело с преимущественными потоками влаги. И это, конечно, особо важ но при движении растворенных веществ, токсикантов, агрохими катов. Остановимся о гидрологии этого явления, его физических механизмах и их описании.

Явление «преимущественных потоков» широко известно, его повсеместное проявление и огромное значение для явлений пе реноса веществ в почве общепризнано. Обсуждают, в основном, три типа преимущественных потоков: потоки по устойчивым мак ропорам (типа биопор), потоки по трещинам и проникновения растворов по типу «пальчатых явлений». В реальных эксперимен тах отмечают их существенно большее количество: потоки по поч венным каналам, гравитационные нестабильные потоки, потоки, связанные с варьированием почвенной плотности, осциллирую щие потоки влаги, кратковременные прерывистые (типа лизимет рических) потоки при смене почвенного материала и т.д.

Как же это явление учитывают в математических моделях? В ряде случаев поступают довольно формально. Несколько в

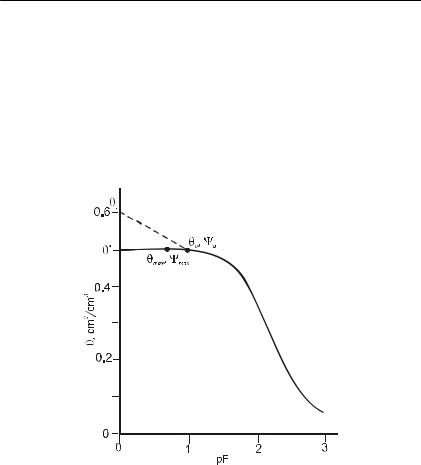
ином виде рассматривают кривую ОГХ, при давлении влаги боль ше, чем давление барботирования. На рис. II.2.2 представлена несколько модифицированная ОГХ, с учетом того, что области давления барботирования (Рб), она не резко и параллельно оси ординат «спадает» до влажности насыщения Θs, а пересекает ось

224

Часть II. Применение математических моделей в почвоведении

влажностей при более высокой влажности, именно за счет мак ропор и трещин. Как правило, авторы это явление не объясняют, ссылаясь на то, что величина влажности в этом случае не реально определенная, а возникающая в процессе расчетов для давлений влаги больше давления барботирования. Она позволяет оцени вать переполнение крупных пор и решать основное уравнение влагопереноса. Это часто используемый формальный подход.

Рис. II.2.2. Модифицированная функция водоудерживания по Ван Генухтену

Есть и более обоснованный подход, подкрепляемый почвен ными измерениями. Действительно, физически межпедное поро вое пространство можно ассоциировать с быстропроводящими порами, а внутрипедное (внутриагрегатное) – с почвенной матри цей. Почвенный и агрегат, и пед (агрегат – для пахотных, а для подпахотных, подгумусовых горизонтов – почвенный пед) имеют повышенную плотность. И если рассчитать порозность почвы в целом (с межпедной порозностью) и вычесть из нее внутриагре гатную (внутрипедную), то мы как раз получим межпедную по розность, то самое межпедное пространство, по которому быстро

225

Математическое моделирование в почвоведении

мигрирует почвенная влага. Тогда приобретают смысл такие мор фологические характеристики почвенных педов и почвенных аг регатов, как их размер, форма (столбчатая, призматическая, пли товидная и др.), прочность и твердость.

В этом случае в меню таблицы гидрологических свойств почв будут представлены следующие столбцы (послойно, для рассмат риваемых слоев/горизонтов почв): «Форма педов» (например, крупноглыбистая, крупноореховатая, мелкостолбчатая, призмати ческая, плитовидная или др.), «Плотность сложения педов» (сли тое, плотное или др.). Понятно, что чем плотнее педы, чем боль ше будет выражена их глыбистость, столбчатость и пр., тем боль ше будут представлены межпедные трещины, межпедное поро вое пространство и тем значительнее будут выражены преимуще ственные потоки в структурных почвах. В самой программе ука занные морфологические характеристики пересчитываются по полуэмпирическим формулам.

И, наконец, наиболее правильным будет подход, когда мак ропористость измеряется непосредственно в полевых условиях. Физики почв научились измерять объем и проводимость «быстро проводящих почвенных каналов с помощью инфильтрометров с вакуумированием. Тогда гидрологическим обеспечением такого рода моделей с двойной пористостью будут являться характери стики, полученные в прямых полевых экспериментах (это важно и особенно ценно!): (1) удельный объем макропор и трещин, быс тропроводящих влагу [см3/см3]; (2) объем замкнутых, не имеющих соединения, макропор в процентах от общего объема пор; (3) проводимость, или влагопроводность обусловленная движением воды по мезо и микропорам, или так называемая матричная вла гопроводность. Такие подходы успешно развивали, в частности Г. В. Стулина с соавторами (2000), представляя в такого рода моде ли массивы уникальных данных прямых измерений макропорис тости, которые определяли на инфильтрометрах. Таким образом в меню таблицы с гидрологическими параметрами появились столбцы с указанием числовых значений макропористости и мат ричной пористости.

226

Часть II. Применение математических моделей в почвоведении

2.4.Начальные и граничные условия

Сзаданием начальных условий все достаточно просто. На чальные условия – это пространственное (по профилю почвы) распределение переменной состояния (температуры, влажности, концентрации вещества пр.) в начальный (нулевой) момент вре мени, с которого начинаются расчеты. Для гидрологических рас четов начальные условия могут быть заданы либо в величинах влажности, либо в величинах давления влаги. Как правило, для расчетов водного режима почв в вегетационный период исполь зуют распределение влажности почвы после весеннего снеготая ния, которое представляет собой распределение влажности, рав ной наименьшей влагоемкости для различных слоев почвенного профиля (экспериментальная информация).

Граничные условия (см. «К вопросу о….»).

Задание граничных условий нередко вызывает трудности, так как в этом случае необходимо совместить математическое уст ройство модели с реальными почвенно гидрологическими усло виями. Попытаемся подробно в этом разобраться.

К вопросу о…

Таким иероглифом китайцы обозначают почву («землю», «плодородие»). Произносится и пишется по английски как «ti» (ти). Этот иероглиф напоминает росток, пробивающийся сквозь ровную поверхность почвы. Конечно, первоначально ие роглифы представляли собой примитивные рисунки. Например, дуга выпуклостью вверх и точки под ней служили изображением неба и капель; такова первоначальная форма иероглифа юй «дождь». Потом, с течением времени рисунки схематизирова

227

Математическое моделирование в почвоведении

лись и в конце концов приобрели современный вид, где от пер воначальной картинки уже ничего и не осталось.

Но для нас важно другое. Посмотрим внимательно на ие роглиф «ти». Да, конечно, прекрасно виден росток, с усилием выбивающийся из поверхности почвы. Но ведь видна и горизон тальная линия снизу, соединенная с линией поверхности почв вертикальной чертой. Две горизонтальные черты, соединен ные вертикальной линией… Неужели древние китайцы имели представление о почве как о некоторой плодородной среде с верхней и нижней границами – верхняя горизонтальная линия, которую пробивает росток, и нижняя горизонтальная линия иероглифа соответственно. И теперь мы снова даем опреде ление почвы как «естественно исторического природного тела […], обладающего верхней и нижней границами…». Только при таком определении почвенного тела можно применить законы неразрывности, баланса, переноса и лишь потом использовать математические модели процессов, протекающих в почве. Так неужели древние китайцы понимали это, понимали необходи мость определять почву по её верхней и нижней границам? Мне иногда становится чуть страшновато от глубины пони мания древними людьми природных процессов.

Условия на верхней границе

Верхние граничные условия – это гидрологические условия на верхней границе почвы. Чаще всего их задают в виде потока вла ги, поступающего в почву (осадки, поливы и пр.) и выходящего из почвы (испарение, транспирация и пр.). В общем виде их называ ют «Атмосферные условия». В этом случае надо задавать испаре ние и/или эвапотранспирацию, осадки, их длительность и количе ство. В некоторых масштабных моделях, в которых расчеты про водятся на несколько лет (прогнозные модели поведения пести цидов в почве, модели циклов органического вещества) требуется задать местоположение (географические координаты). Тогда по модели можно ориентироваться на среднемноголетние метеоус ловия (среднемноголетние осадки, испарения и прочее), либо на

228

Часть II. Применение математических моделей в почвоведении

«влажные годы» или «сухие годы», т.е. годы с определенной обеспеченностью осадков.

В ряде случаев услуга «Атмосферные условия» может распа даться на две: «Атмосферные условия со стоком» и «Атмосфер ные условия без стока». В первом случае, на поверхности почвы не образуется избыток воды, который не впитывается в почву, стекает по поверхности в пониженные элементы рельефа. А во втором, образуется слой воды с некоторым напором, который надо указывать при работе с моделью.

К верхним граничным условиям мы еще вернемся при рас смотрении метеоблока моделей.

Условия на нижней границе

Нижние граничные условия – это математическое выражение для описания гидрологических условий на нижней границе поч вы. Понятно, что для точной установки условий на нижней грани це надо знать почвенный объект, какова его гидрология. С другой стороны следует знать особенности математического описания того или иного граничного условия, чтобы применить его к своему объекту.

На нижней границе могут быть условия I, II, III рода.

Условие I рода, «постоянное». Оно выражается в виде

θ(zend ,t) =θ0 и указывает, что влажность или давление влаги на нижней границе почвы ( zend ) в течение времени (t) постоянны.

Это условие названо в честь немецкого математика Лежён Дирихле Иоганна Петера Густава условием Дирихле (см «К вопро су о….»). Это условие не обязательно и записывается как влаж ность или давление – есть константы. В ряде случаев это условие записывается в виде известной функции влажности или давления влаги от времени.

Когда справедливо это условие? Прежде всего, в гидроморф ных почвах, когда нижняя граница приходится на грунтовые воды, на глубине, где влажность почвы постоянна и равна влажности

229

Математическое моделирование в почвоведении

насыщения (полной влагоемкости). Кроме того, постановка этого условия возможна и в автоморфных степных почвах, когда влаж ность практически не изменяется на определенной глубине в те чение сезона. Так, в черноземах, в которых имеется так называе мый «мертвый горизонт» (по Г.Н. Высоцкому, 1900). Если воз можно рассматривать нижнюю границу почвы

∂θ(zend ,t) =0

∂z

именно в этом «мертвом» горизонте, то вполне возможно поста вить постоянную влажность на нижней границе, т.е. использовать условие Дирихле.

К вопросу о….

Великие математики

Лежён Дирихле Иоганн Петер Густав (13 февраля 1805 — 5 мая 1859). Его предки были выходцами из бельгийского городка Ришле (Richelet). Поэтому и имя, и фамилию Лежёна Дирихле можно перевести с французского как «молодой человек из Риш ле» (фр. Le Jeune de Richelet). Математики почитают его за многие достижения. Немудрено: он был учеником Георга Ома, его приглашает Александр фон Гумбольд в Бреслау, затем он уже профессор Берлинского университета, а с 1855 г. преемник великого Гаусса и профессор высшей математики в Гёттинген ском университете. Великий математик «молодой человек из Ришле»!

Карл Готфрид Нейман (7 мая 1832, Кёнигсберг — 27 марта 1925, Лейпциг) — немецкий математик, профессор универси тетов в Базеле (с 1863), Тюбингене (с 1865) и Лейпциге (с 1868). Именно он детально исследовал вторую краевую задачу, кото рая в современной математике так и называется, «задача Неймана». Занимался он также проблемами физики, в основ ном, учением об электричестве.

230