мат. модел в почв

Часть II. Применение математических моделей в почвоведении

распространяется тепло из слоя в слой: κi +12 и κi −12 . Для примера,

на границах нашей толщи (от i 1 до i+1) никаких тепловых явлений не происходит, нет подтоков тепла и, соответственно, нет изме нения температуры. В этом случае, нам известно всё эксперимен тальное обеспечение (коэффициенты температуропроводности слоев, начальные и граничные условия) для расчета тепла в i ом слое в следующий момент времени (j+1). Поэтому по вышеприве денному уравнению можно рассчитать температуру в i м слое в заданный j+1 момент времени (в будущем), задав промежуток времени t и толщину слоев z .

Получается, что прогнозные расчеты температуры аналогич ны прогнозированию передвижения влаги в почве с помощью се точной схемы расчета. И здесь мы можем рассчитать температуру i го слоя, задавая z и t , зная значения коэффициента темпера туропроводности для соответствующих слоев. Заметим, что в экс периментальное почвенное обеспечение моделей теплопереноса вводятся не отдельные значения коэффициента температуропро водности или теплопроводности (они связаны через значения те плоемкости), а их зависимости от влажности (в табл. II.2.4 они указаны в виде b1, b2, b3). Поэтому в тепловой блок моделей пе редвижения веществ в почве обязательно входят указанные зави симости. Например, исходные данные о слоях почвы и о тради ционных теплофизических свойствах (теплоемкость твердой, жидкой фаз и органического вещества) следует вводить в табли цы, аналогичные приведенной ниже.

Таблица II.2.4

Пример теплофизических параметров почвы при моделировании тем пературного режима в слоистой почве

241

Математическое моделирование в почвоведении

Глава 3. Аппроксимация экспериментальных данных

3.1.Понятие об аппроксимации экспериментальных данных.

3.2.Основные функциональные зависимости, используемые

вестествознании, их классификация.

3.3.Элиминирование параметров аппроксимации.

3.4.Оценка качества аппроксимации.

3.5.Подбор параметров аппроксимации для выбранной функции

ипроцедура сканирования для поиска параметров.

3.6.Сравнение параметров аппроксимации и выбор наилучшей функции для конкретной выборки.

3.7.Анализ различия моделей и выбор лучшей. Непараметрический критерий Вильямса Клюта.

3.1.Понятие об аппроксимации экспериментальных

данных

Мы знаем, что основой расчета переноса влаги в почве явля ется уравнение Ричардса, в котором одним из членов является

дифференциальная влагоемкость, C(θ,Pк с) ) = dθ . Эта величина dPк с

получается дифференцированием основной гидрофизической ха рактеристики, которая определяется экспериментально. Конечно же, дифференцировать зависимость, представленную отдельны ми экспериментальными точками, невозможно. Необходимо эту зависимость описать некоторой функцией, т.е. подобрать вид функции и некоторые её параметры таким образом, чтобы график функции проходил ближе всего к экспериментальным данным во всей области их определения. Некоторые виды функций для опи сания ОГХ мы разбирали выше.

242

Часть II. Применение математических моделей в почвоведении

Аналогичные процедуры проводят с моделью термопереноса

в почвах. В этой модели используется основное уравнение тепло

переноса, dT = κ d2T , в котором функция температуропроводно dt dz2

сти представлена, как зависимость от влажностиκ= f (θ) . Эта функция также нелинейная и в процессе работы модели должна быть введена в препроцессор в виде функциональной зависимо сти, наиболее подходящей для описываемого почвенного слоя.

Основная задача данного раздела – научиться подбирать вид нелинейной функции и некоторым методам определения ее па раметров для конкретной экспериментальной выборки, т.е. про водить процедуру аппроксимации.

Таким образом, задача аппроксимации сводится к последо вательному выполнению двух операций:

1. Установление вида зависимости y=φ(х) – процедура, кото рая осуществляется, как правило, опытным путем (на основе сво его опыта или опыта коллег), но по определенным правилам.

2. Определение численных значений неизвестных парамет ров выбранной функции (b1, b2, b3 …bn), при которых задача сгла живания экспериментальных данных решается наилучшим обра зом (анализ ошибок аппроксимации для точек y1, y2, y3 …yn).

243

Математическое моделирование в почвоведении

3.2.Основные функциональные зависимости, исполь зуемые в естествознании, их классификация

Согласно общепринятому определению, функция – одно из основных понятий математики – выражает зависимость одних пе ременных от других. Если величины x и у связаны так, что каждо му значению x соответствует определённое значение у, то у назы вают функцией аргумента x.

В экспериментах, как правило, мы задаем величину х и полу чаем соответствующую ей величину функции y. Или, как говорят математики, функцию отклика. Например, мы определяем основ ную гидрофизическую характеристику (ОГХ) методом мембранно го пресса. Первоначально насыщенный образец находится на ке рамической пластине. Затем мы задаем над образцом почвы по вышенное газовое давление, и из образца вытекает вода до тех пор, пока внешнее заданное давление не сравняется с давлением почвенной влаги. В этот момент мы определяем влажность об разца. В результате мы получили одну из точек на кривой ОГХ – зависимость влажности почвы y от давления влаги х. Ступенчато повышая давление влаги х над образцом, мы получаем соответ ствующие значения влажности y. Эти пары значений будут харак терными именно для испытуемого образца. Полученные данные мы должны аппроксимировать некоторой функцией. Начнем с первой части процедуры аппроксимации – установление вида за висимости y=φ(х).

Все множество функций, применимых к описанию явлений в природе, можно разделить на несколько больших групп в зави симости от направленности процесса:

I.Монотонные

1.Возрастающие

2.Убывающие

II. С одним экстремумом

III. С несколькими экстремумами

IV. С изломом

244

Часть II. Применение математических моделей в почвоведении

Монотонные (убывающие и возрастающие) функции

Все множество убывающих и возрастающих функций можно разделить на пять типов:

1.Линейная

2.Степенная (за исключением параболы)

3.Показательная и экспоненциальная

4.Логарифмическая

5.Логистическая

Линейная функция

Линейная функция имеет вид y =b1 +b2 x , графически это прямая линия.

Она употребляется для описания пропорциональной зависи мости. Однако, для описания зависимостей многих почвенных процессов, таких как ОГХ, функция влагопроводности, зависимо сти температуропроводности от влажности и множества других этот вид функции непригоден – эти зависимости нелинейны и для их описания требуются другие виды. В науках об окружающей нас природе линейные функции используются нечасто.

Степенная функция

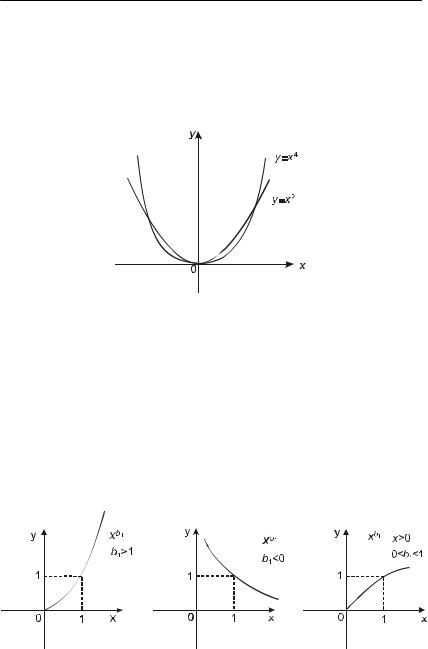
Самым простой и распространенной функцией среди степен ных является квадратичная с графиком, называемым параболой (рис. II.3.1.). Здесь надо отметить, что крутизна ветвей этой пара болы будет тем выше, чем выше степень (приведены примеры для степени, равной 2 и 4). И график этот будет симметричен от носительно оси y. Но только в том случае, если показатель степе ни четный, тогда и функция называется четной.

В почвоведении, где предикторы представлены, как правило, положительными числами, степенная функция выглядит несколь

x может быть любым действительным числом при показателе

245

Математическое моделирование в почвоведении

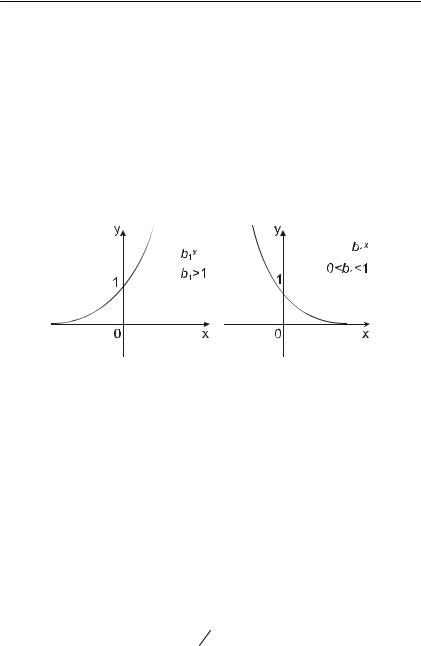
степени > 0 и ≠ 0 при показателе степени < 0 (рис. II.3.2.). Для лю бых b1 график функции проходит через точку (1; 1). В указанных уравнениях степенной функции первую называет однопарамет рической, а вторую – двухпараметрической.

Рис. II.3.1. График зависимости степенной функции (парабола)

Графики степенной функции при положительном показателе b1 называются параболами порядка b1, а при отрицательном – ги перболами порядка b1. Таким образом, смена знака показателя при аргументе c положительного на отрицательный превращает функцию возрастающую в убывающую. Это правило нам уже встречалось выше (см. линейную регрессию): «Смена знака перед аргументом превращает функцию из убывающей (если был ми нус) в возрастающую».

Рис. II.3.2. Примеры графиков степенной функции

246

Часть II. Применение математических моделей в почвоведении

Степенная функция очень широко используется в почвоведе нии. Например, уравнение Фрейндлиха для описания процесса сорбции (Орлов, 1992): Q =m Cn , где Q – концентрация сорбиро ванного иона [моль/100 г почвы], С – концентрация иона в контак тирующем растворе [моль/л], m и n – эмпирические параметры, характерные для каждого почвенного образца. Важен и еще один момент. Во многих случаях эмпирические параметры носят физи ческий смысл. В частности, в указанном степенном уравнении Фрейндлиха, несмотря на его эмпирический характер, степенной параметр n (показатель степени), как было показано Г. Спозито, можно рассматривать как показатель неоднородности сорбцион ных центров. Он приближается к 0 по мере возрастания неодно родности и стремится к 1 при увеличении их однородности. Это означает, что определение параметров аппроксимации имеет не только практическое значение (использование в математических моделях), но и для понимания и сравнения физических явлений. Однако чтобы понять физический смысл и значение регрессион ных коэффициентов, надо закладывать специальные эксперимен ты, анализировать поведение функции в различных условиях. В самом общем случае, эти коэффициенты, как и многие регресси онные коэффициенты, безразмерны и далеко не всегда имеют физический смысл. При использовании регрессионного уравне ния нужно указывать не только его вид и размерность функции отклика и факторов (предикторов), но и границы области опреде ления факторов (обязательно!).

Показательная и экспоненциальная функции

При рассмотрении многих природных процессов и явлений может оказаться полезным рассмотрение показательной функции b1x , где b1 основание показательной функции имеет только по ложительные значения, а в качестве переменной выступает пока затель степени (рис. II.3.3).

Частным (но наиболее употребительным!) случаем показа тельной функции является функция экспоненциальная

247

Математическое моделирование в почвоведении

y =b1 exp(b2 x), где exp – основание натуральных логарифмов (e = 2.7182...). Особым свойством экспоненты является то, что она возрастает или убывает быстрее, чем степенная функция.

Используя функцию натурального логарифма ln x, можно вы разить показательную функцию с произвольным положительным

основанием b1 черезэкспоненту b1 x = ex ln b1 . Эта связь позволяет в большинстве аппроксимаций ограничиться изучением свойств экс поненты.

Рис. II.3.3. Пример графиков показательной функции

И опять работает правило «знака перед аргументом»: плюс – функция возрастающая, минус – убывающая.

Экспоненциальная функция сначала довольно быстро возрас тает (или убывает при минусе перед аргументом), а затем посте пенно и плавно «выходит на плато», что указывает на наступле ние некоторого равновесия. Эти свойства показательной и экспо ненциальной функций позволяют использовать их во многих об ластях науки, в т.ч. при описании химических реакций, роста чис ленности микроорганизмов и др. Экспоненциальные функции очень важны, поскольку они описывают такие физические явле ния, как радиоактивный распад. Эту функцию используют для оп ределения количества радиоактивного вещества, оставшегося к

моменту t по формуле N =N0 2− t T1/2 , где N0 – начальное количество вещества, T1/2 – период полураспада радиоактивного вещества, т.е. промежуток времени, в течение которого распадается поло

248

Часть II. Применение математических моделей в почвоведении

вина начального количества ядер радиоактивного изотопа. В аг рохимии для токсикантов, агрохимикатов, и др. используют тер мин период полуразложения, хотя английский вариант этого тер мина один: Half life. Запомним эту функцию, она очень полезна.

Описывая экспоненциальные функции нельзя не упомянуть часто встречающее распределение (или функцию) Вейбулла. В несколько упрощенном виде эта функция записывается

y=1 −exp −(x / b1 )b2 .

Впочвоведении она встречается достаточно часто, например, для описания скорости распада агрегатов в воде и распределения гранулометрических частиц, хотя строгого, подходящего для большинства почв, уравнения для гранулометрического состава не предложено. Все же упомянем распределение Вейбулла и для распределения частиц по гранулометрическому составу:

y =b1 +(1 −b1 ) 1 −exp(−b2 xb3 ) .

Логарифмическая функция

Логарифмическая функция с основанием b1, это функция вида logb1 x , где b1 >0 и ≠ 1. Если b1 > 1, то функция на всей области оп

ределения возрастает, а если 0 < b1 < 1 убывает (рис. II.3.4.). Осо бенностью логарифмической функции является то, что значение 0 функция принимает в точке х = 1 при любом b1 > 0.

Рис. II.3.4. Примеры графиков логарифмической функции

249

Математическое моделирование в почвоведении

При работе с логарифмической функцией может оказаться полезным тот факт, что графики показательной вида b1x и лога рифмической функций, имеющих одинаковое основание, сим метричны относительно биссектрисы у = х, т.е. функция y =logb x

обратна показательной функции y =bx (рис. II.3.5). В большинстве случаев используют показательную или экспоненциальную функ ции.

В научных исследованиях логарифмическую функцию исполь зуют широко: в астрономии – для измерения величины яркости звезд, для описания спиральной формы галактик, в биологии – при описании формы ракушек улиток, рогов животных, паутин и т.д., в физике – для оценки громкости шума, в экономике – при расчетах роста денежных капиталов и др.

Рис. II.3.5. Примеры графиков показательной и логарифмической функ ций

Но наиболее часто логарифмическая функция используется в почвоведении при характеристике реакций первого порядка

где С0 – начальная концентрация некоторого вещества, Сi – кон центрация этого вещества в момент времени t, а k1 – постоянная первого порядка. Все эти названия («кинетика первого порядка», «постоянная первого порядка» и др.) широко используются при математическом описании процессов разложения или трансфор мации некоторых веществ в почве (например, сложных органиче ских веществ и др.). Сейчас же для нас важно, что и показатель

250