
Методика решения задач по оптике для студентов инженерных специальностей
.pdf

9*. Ответ: β ≈ 5,2 10−1рад ≈ 30°.
***************
Задача37
Установка для получения колец Ньютона освещается светом от ртутной дуги, падающим по нормали к поверхности пластинки. Наблюдение ведется в проходящем свете. Какое по порядку m светлое кольцо, соответствующее линии λ1 = 583,4 нм,
совпадает со следующим светлым кольцом, соответствующим
линии |
λ2 = 577 нм? |
|
|
|
|
|
|
|
|
|
||
1*. Дано: |
|
|
|
|
|
|
Решение. |
|
|
|||
λ = 583,4 нм = 5,834 10-7м, |
2* ─── |
|
|
|
|
|||||||
1 |
|
|
|
|
|
4*. |
|
Составим |
полную |
|||
|
|
|
|
|
|
|
||||||
λ2 = 577 нм = 5,77 10 |
-7 |
м. |
систему |
|
уравнений |
|
для |
|||||
|
нахождения |
искомой |
величины |
|||||||||
|
|
|
|
|
|
m : |
|
|
|
|
|
|
m 10 – ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
rm = Rλ1m, |
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
′ |
|
= Rλ2 (m +1), |
||
|
|
|
|
|
|
(2) |
|
|||||
|
|
|
|
|
|
rm+1 |
||||||
|
|
|
|
|
|
|
(3) |
′ |
|
= rm . |
|
|
|
|
|
|
|
|
|
rm+1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Система |
трех уравнений |
(1) – |
(3) |
не |
замкнута, так |
как |
||||||
содержит четыре неизвестные величины: |
′ |
+1, R, m . |
||||||||||
rm , rm |
||||||||||||
Однако |
уравнения |
(1), (2) |
линейно зависимы относительно |
|||||||||
величин |
rm , |
′ |
R , поэтому система |
однозначно разрешима |
||||||||
rm+1, |
||||||||||||
относительно искомой величины m . |
|
|
|
|
|
|
||||||
9*. Ответ: |
|
|
m = 9,0 101 = 90. |
|
|
|
|
|
||||
|
|
|
|
*************** |
|
|
|
|
|
|||
|
|
|
|
|
Задача38 |
|
|
|
|
|
||
Абсолютно |
черное |
тело |
цилиндрической |
формы |
радиуса |
|||||||
R = 20 см |
высотой |
|
H = 120 мм |
поддерживается |
при |
|||||||
температуре |
T = 1002°C . Вычислить энергию Q , излучаемую |
|||||||||||
этим телом за промежуток времени t |
= 1 мин. |
|
|
|
||||||||
10Необходимонайтицелуючастьчисла!
-141 -

1*. Дано: |
|
|
|
|
|
|
|
Решение. |
|
||||||||
R = 20 см = 0,2 м, |
|
|
2R |
|
2*. |
|
|
|
|
|
|
|
|
||||
H = 120 мм = 1,2 10-1м, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
H |
|
|||||||
T = 1002°C = (1002 + |
273)K , |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
t = 1 мин = 6 101c . |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||
Q – ? |
|
−8 |
Вт |
|
|
|
|
|
|
|
|
T |
|
||||
σ = 5,67 10 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
м2 K4 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4*. |
Составим |
полную |
систему |
(1) |
|
|
Q = E(T ) S t, |
||||||||||
уравнений |
для |
нахождения |
искомой |
|
|
|
|
E(T )= σT 4 , |
|||||||||
величины Q : |
|
|
|
|
|
|
|
(2) |
|
|
|
||||||
Система трех уравнений (1) – (3) |
(3) |
|
|
|
S = 2πR(H + R). |
||||||||||||
замкнута, так как содержит три |
|
|
|
|
|
|
|
|
|
||||||||
неизвестные величины: Q, E(T ), S . |
|
|
|
|
|
|
|
|
|
|
|||||||
9*. Ответ: |
|
|
Q ≈ 3,6 104 Дж = 36 кДж. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
*************** |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Задача39 |
|
|
|
|
|
|
|
|
|
||
Фотон с энергией W = 0,25 |
МэВ рассеялся на первоначально |
||||||||||||||||
покоившемся свободном электроне. Определить кинетическую |
|||||||||||||||||
энергию Te электрона отдачи, если длина волны рассеянного |
|||||||||||||||||
фотона изменилась на величину k = 20%. |
|
|
|
|
|
|
|
|
|||||||||
1*. Дано: |
|
|
|
|
|
|
Решение. |
|
|
|
|||||||
W = 0,25 МэВ = |
|
|
2*. |
единичный |
|
|
|
вектор |
|
||||||||
= 2,5 1,6 10 |
−14 |
Дж, |
|
|
|
|
|
|
|
|
|
' |
|
||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
||
k = 20%. |
|
|
|
|
|
|
(h/λ)k |
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ |
|
|
|||
Te – ? |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
электрон отдачи |
|
||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
- 142 - |
|
|
|
|
|
|
|
|
|
|

4*. Составим полную систему уравнений для нахождения |
||||||||||||
искомой величины Te : |
|
|
|
[T = mc2 − m |
c2 ] |
|
||||||
(1) |
|
hc − hc = T , |
|
|
||||||||
|
|
λ |
|
λ′ |
|
e |
|
e |
|
e |
|
|
|
|
λ′ = |
λ(1 + k 100), |
|
|
|
|
|
|
|||
(2) |
|
|
|
|
|
|
||||||
|
|
|
hc |
|
|
|
|
|
|
|
|
|
|
|
W = |
, |
|
|
|
|
|
|
|||
(3) |
|
λ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hc |
|
|
|
|
|
|
|
||
|
|
W ′ = |
. |
|
|
|
|
|
|
|||
(4) |
λ′ |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Система четырех уравнений (1) – (4) замкнута, так как |
||||||||||||
содержит четыре неизвестные величины: λ, |
λ′, W ′, Te . |
|
||||||||||
9*. Ответ: |
|
|
Te ≈ 6,7 10−15 Дж ≈ 41,9 кэВ. |
|
|
|
||||||
|
|
|
|
|
|
*************** |
|
|
|
|
||
|
|
|
|
|
|
Задача40 |
|
|
|
|
|
|
1s-электрон |
( n =1, |
l = 0) атома |
водорода |
поглотил фотон |
с |
|||||||
энергией Е = 12,1 эВ |
и |
перешел |
в возбужденное |
состояние |
с |
|||||||
максимально возможным орбитальным квантовым числом. |
||||||||||||
Определить |
изменение |
|
момента |
импульса |
Ll |
орбитального |
||||||
движения электрона. |
|
|
|
|
|
|
|
|
|
|||
1*. Дано: |
|
|
|
|
|
|
|
|
Решение. |
|
||
l = 0, |
|
|
|
|
|
|
|
2*. |
|
|
|
|
Е = 12,1 эВ = |
|
|
|
|
|
|
|
|
ml |
|
||
= 1,21 1,6 10-18 Дж. |
|
|
например, lmax= l =2 |
|
||||||||
|
|
|
|
|
|
+2 |
|
|||||
|
|
|
|
|
|
|
Llx |
d l=2 |
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
||
Ll – ? |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
h = 6,63 10−34 Дж с, |
|
|
Lls |
s l=0 |
|
|
|
|
||||
h = h (2π), |
|
|
|
|
|
|
|
|
|
|
|
|
R = 3,29 1015с-1. |
|
|
|
|
|
|
|
|
|
|
||
4*. Составим полную систему уравнений для нахождения |
||||||||||||
искомой величины |
Ll : |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
- 143 - |
|
|
|
|
|
|

|
(1) |
Ls = h |
l(l + 1), |
|
|
|
|||||
|
|
l |
|
lmax (lmax + 1), |
|
|
|
||||
|
Llx |
|
|
|
|
||||||
|
(2) |
= h |
|
|
|
||||||
|
|
L |
= Lx − Ls , |
|
|
|
|
||||
|
(3) |
|
|
|
|
||||||
|
|
|
|
l |
l |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
||
|
(4) |
|
|
|
|
||||||
|
ν = |
R |
2 − |
n |
2 |
, |
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
||
|
(5) |
E = hν , |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lmax = n −1. |
|
|
|
|
|
||||
|
(6) |
|
|
|
|
|
|||||
Система шести уравнений (1) – (6) замкнута, так как |
|||||||||||
содержит шесть неизвестных величин: |
Lsl , Llx , |
L, ν , |
lmax , n. |
||||||||
9*. Ответ: |
|
|
Ll ≈ 3,1 10−34 Дж с. |
|
|
|
|||||
|
|
|
*************** |
|
|
|
|||||
|
|
|
Задача41 |
|
|
|
|
||||
Расстояние от предмета до экрана S = 90 см. Между предметом |
|||||||||||
и экраном необходимо поместить собирающую линзу с |
|||||||||||
фокусным расстоянием F = 20 см. |
|
На каком расстоянии d от |
|||||||||
предмета необходимо ее поместить, чтобы получить на экране |
|||||||||||
четкое изображение предмета? Сколько решений имеет задача? |
|||||||||||
1*. Дано: |
-1 |
|
|
2*. |
|
|
|
Решение. |
|
|
|
S = 90 см = 9 10 |
м, |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
F = 20 см = 2 10-1м. |
B |
|
|
|
|
экран |
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
2F |
|
|
|
F |
|
2F |
|
|
|
|
A |
. .F |
SF |
.A' |
B'. |
||||
|
|
|
|
|
|
d |
|
|
f |
|
|
d – ? |
|
|
Один из возможных вариантов |
- |
предмет |
||||||
|
|
|
находится за двойным фокусным расстоянием, |
||||||||
|
|
|
другой - между F и 2F (на рис. не показан) |
||||||||
4*. Составим полную систему уравнений для нахождения |
|||||||||||
искомой величины d : |
|
1 |
+ 1 |
|
1 , |
|
|
|
|||
|
|
|
(1) |
= |
|
|
|
||||
|
|
|
|
d |
f |
|
F |
|
|
|
|
|
|
|
(2) |
d + f = S. |
|
|
|
||||
|
|
|
|
- 144 - |
|
|
|
|
|
|
|

Система двух уравнений (1) – (2) замкнута, так как содержит |
||||||||||||
две неизвестные величины: d, |
f . |
|
|
|
|
|
||||||
|
|
|
|
|
10 |
−1 |
м= 60 см, |
|
|
|
||
9*. Ответ: |
|
d = |
6,0 |
|
|
|
|
|||||
|
|
|
|
−1 |
|
|
|
|
|
|
||
|
|
|
|
|
10 |
м = 30 см. |
|
|
|
|||
|
|
|
3,0 |
|
|
|
|
|||||
|
|
|
*************** |
|
|
|
||||||
|
|
|
|
Задача42 |
|
|
|
|
||||
Два параллельных световых пучка, отстоящих друг от друга на |
||||||||||||
расстоянии |
L = 5 см, падают |
нормально на боковую |
грань |
|||||||||
равнобедренной кварцевой призмы, имеющей показатель |
||||||||||||
преломления n =1,5 и преломляющий угол α = 30o. Определить |
||||||||||||
оптическую |
разность |
хода |
|
d |
этих |
пучков |
на |
выходе |
их из |
|||
призмы. |
|
|
|
|
|
|
|
|
|
|
|
|
1*. Дано: |
|
|
|
|
|
|
|
|
Решение. |
|
|
|
L = 5 см = 5 10-2м, |
|
|
|
|
|
|
N |
|
|
|
||
|
1 |
|
|
|
ε=0 |
α |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
ε = 0o, |
|
|
2 |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n =1,5, |
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
α = 30o. |
|
|
|
|
|
|
|
n |
|
α |
|
|
d – ? |
|
|
|
|
|
|
|
|
π/2 |
B |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Q |
|
|
|
|
|
|
d |
M |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4*. Составим полную систему уравнений для нахождения |
||||||||||||
искомой величины |
d : |
|
|
d = |
d′ n, |
|
|
|
||||
|
|
|
(1) |
|
|
|
|
|
||||
|
|
|
|
|
|
d′ = Ltgα. |
|
|
|
|||
|
|
|
(2) |
|
|
|
|
|||||
Система двух уравнений (1) – (2) замкнута, так как содержит |
||||||||||||
две неизвестные величины: |
′ |
d . |
|
|
|
|
||||||
d |
, |
|
|
|
|
|||||||
9*. Ответ: |
|
d ≈ 4,3 10−2м = 4,3 см. |
|
|
|
|||||||
|
|
|
*************** |
|
|
|
||||||
|
|
|
|
|
- 145 - |
|
|
|
|
|||

Задача43
Мощность излучения раскаленной металлической поверхности некоторого тела равна N = 0,67 кВт. Температура поверхности
его T = 2500 K , площадь поверхности |
S = 10 см2. Определить |
||
степень черноты k этого тела. |
|
|
|
1*. Дано: |
|
Решение. |
|
N = 0,67 кВт = 6,7 102Вт, |
2* ─── |
|
|
T = 2500 K = 2,5 103 K , |
4*. |
Составим |
полную |
S = 10 см2 = 10−3м2 . |
систему |
уравнений |
для |
нахождения искомой величины k : |
|||
|
(1) |
E(T )= kσT 4 , |
|
k – ? |
|
||
|
E(T )= N S . |
|
|
σ = 5,67 10−8 Вт (м2 К4 ). |
(2) |
|
|
Система двух уравнений (1) – (2) замкнута, так как содержит |
|
две неизвестные величины: E(T ), k . |
|
9*. Ответ: |
k ≈ 3,0 10−1 = 0,3. |
|
*************** |
Задача44
На идеально отражающую поверхность (коэффициент отражения R =1) под углом i = 0 падает свет; поток излучения составляет Фe = 0,45 Вт. Определить силу давления F , испытываемую этой
поверхностью.
1*. Дано: |
2* ─── |
|
R =1, |
4*. Составим полную систему уравнений |
|
i = 0 , |
для нахождения искомой величины F : |
|
(1) |
p = w(1 + R)cos2 i, |
|
Фe = 0,45 Вт. |
|
Фе |
|
||
|
(2) |
wc = S , |
|
(3) |
|
F – ? |
F = pS. |
|
c = 3 108м/с. |
|
|
|
|
|
|
|
|
Система трех уравнений (1) – (3) не замкнута, так как содержит четыре неизвестные величины: p, w, S, F . Однако
уравнения (1) - (3) линейно зависимы относительно величин
- 146 -

p, S, F . Решение системы получается последовательной подстановкой в (3) уравнений (1), (2).
9*. Ответ: F = 3,0 10−9 Н = 3 нН.
***************
Задача45
Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 2 кВ. Неопределенность скорости таких моноэнергетических электронов составляет k = 0,1% от ее числового значения. Определить неопределенность координаты х этих электронов.
1*. Дано: |
|
|
|
|
2* ─── |
|
|
Решение. |
|
|
|||
U = 2 кВ = 2 103 В, |
|
|
|
|
|
|
систему |
||||||
υ 100 = k , |
|
|
|
4*. |
Составим полную |
||||||||
|
|
|
уравнений |
для |
нахождения |
искомой |
|||||||
υ |
|
|
|
|
|||||||||
|
|
|
|
величины |
х: |
|
|
|
|
|
|
|
|
k = 0,1% . |
|
|
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
meυ |
|
= eU, |
eU << mec2 , |
||||
|
|
|
|
|
(1) |
|
|
||||||
|
|
|
|
|
2 |
|
|
||||||
х – ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
px ≥ h, |
|
|
|
|||||
h = 6,63 10 |
−34 |
Дж |
|
с, |
(2) |
|
|
|
|||||
|
|
υ 100 = k, |
|
|
|
||||||||
me = 9,1 10−31кг, |
|
|
(3) |
|
|
|
|||||||
e = 1,6 10−19 Кл, |
|
|
|
υ |
|
|
|
|
|
|
|
||
|
|
|
px = me |
υ. |
|
|
|
||||||
h = h (2π). |
|
|
|
|
(4) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Система четырех |
уравнений (1) – (4) замкнута, так как |
||||||||||||
содержит четыре неизвестные величины: |
px , |
υ, υ, |
x . |
||||||||||
9*. Ответ: |
|
|
|
x ≈ 4,4 10−15м = 4,4 фм. |
|
|
|
||||||
***************
Задача46
Точечный источник света и его изображения, полученные путем однократного отражения света от двух непараллельных плоских зеркал, поставленных под углом β = 80°образуют треугольник
BSZ с углом S у источника. Угол Z в указанном треугольнике равен δ = 30o. Определить угол γ треугольникa BSZ при вершине B.
- 147 -

1*. Дано: |
|
|
|
|
|
2*. |
.K |
Решение. |
|
|
|
|||||
|
|
4π |
|
|
|
|
S-источник |
|
|
|
||||||
β = 80° = |
9 |
|
рад, |
|
B |
|
γ |
.α |
π/2 |
M |
|
|
|
|||
δ = 30o = π рад. |
|
|
. |
|
ε |
|
|
. |
|
|
|
|||||
|
|
6 |
|
|
|
|
|
|
|
.F |
|
|
ϕN |
|
.Z |
|
γ – ? |
|
|
|
|
|
|
|
|
|
|
|
. |
δ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
ребро |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O. |
двугранного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угла зеркал |
|
|
|
|
4*. Составим полную систему уравнений для нахождения |
||||||||||||||||
искомой величины γ: |
|
|
|
|
|
|
|
|
|
|
||||||
(1) |
|
α+ π 2 +π 2 + β = 2π, |
|
|
|
(SKOM) |
|
|||||||||
(2) |
γ + δ+ α = π. |
|
|
|
|
|
|
(SBZ) |
|
|
||||||
Система двух уравнений (1) – (2) замкнута, так как содержит |
||||||||||||||||
две неизвестные величины: α, γ. |
|
|
|
|
|
|
|
|
||||||||
9*. Ответ: |
|
|
γ = 5π рад ≈ 8,7 10-1 |
= 50o. |
|
|
|
|
||||||||
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*************** |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Задача47 |
|
|
|
|
|
|
|||
На |
дифракционную |
|
решетку |
нормально |
|
падает |
||||||||||
монохроматический свет. В спектре, полученном с помощью |
||||||||||||||||
этой дифракционной решетки, |
некоторая |
спектральная |
линия |
|||||||||||||
наблюдается в первом |
порядке m =1 под |
углом |
|
o |
′ |
|||||||||||
ψ =11 20 . |
||||||||||||||||
Определите наивысший порядок спектра mmax , в котором может |
||||||||||||||||
наблюдаться эта линия. |
|
|
|
|
|
|
|
|
|
|
||||||
1*. Дано: |
|
|
|
|
|
|
|
Решение. |
|
|
|
|||||
m =1, |
|
|
|
|
|
|
2* ─── |
|
|
|
|
|
|
|||
o |
′ |
= |
11,33 |
o |
. |
|
|
|
|
|
|
|
|
|
|
|
ψ =11 20 |
|
|
|
|
|
|
|
|
|
|
|
|||||
11 mmax – ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
11 Следуетискатьцелуючастьчисла!
- 148 -

4*. Составим полную систему уравнений для нахождения искомой величины mmax :
(1) |
d sinψ = mλ, |
|
|
||
(2) |
d sinψ |
max |
= m |
max |
λ, |
|
|
|
|
||
|
ψmax ≤ π 2. |
|
|
||
(3) |
|
|
|||
Система трех уравнений (1) – (3) не замкнута, так как содержит четыре неизвестные величины: d, λ, ψmax , mmax .
Однако уравнения (1) и (2) линейно зависимы относительно d, λ, поэтому указанная система однозначно разрешима относительно
d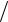 λ, ψmax , mmax .
λ, ψmax , mmax .
9*. Ответ: mmax = 5,0.
***************
Задача48
При нагревании серого тела частота, на которую приходится
максимум излучательной |
способности, |
|
изменилась |
от |
|||||||||||
ν |
1 |
= 1014 Гц до ν |
2 |
= 5 1014 |
Гц, а степень черноты – от k |
= 0,5 |
|||||||||
|
|
|
|
|
|
θ |
|
|
|
|
|
1 |
|
||
до |
k2 = 0,4. Во сколько |
раз |
увеличилась при |
этом |
|||||||||||
интегральная излучательная способность тела? |
|
|
|||||||||||||
1*. Дано: |
|
|
2* ─── |
|
Решение. |
|
|
||||||||
ν1 = 1014 Гц, |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
4*. Составим полную систему уравнений |
||||||||||
ν2 = 5 1014 Гц, |
|
для нахождения искомой величины θ: |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
(1) |
ν |
T |
|
′ |
|
|
||
|
|
|
|
|
|
|
|
= b , |
|
||||||
k1 = 0,5, |
|
|
|
|
|
1 |
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
−1 |
|
′ |
|
|||||
|
|
|
|
|
|
(2) |
|
|
|
|
|
||||
|
|
|
|
|
|
ν2T2 |
|
= b |
, |
|
|||||
k2 = 0,4. |
|
|
|
|
|
E1 = k1σT14 , |
|
||||||||
|
|
|
(3) |
|
|||||||||||
|
|
|
|
|
|
(4) |
E |
|
|
= k σT 4 , |
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
θ – ? |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
E2 . |
|
|
|||||
|
|
|
|
|
|
(5) |
θ = |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
E1 |
|
|
||
|
|
Система пяти уравнений (1) – (5) замкнута, так как |
|||||||||||||
содержит пять неизвестных величин: T1, |
Т2 , |
E1, E2 , θ . |
|
||||||||||||
- 149 -
